SCIENZE E TECNOLOGIE INFORMATICHE

Equazioni di primo grado a coefficienti frazionari

Pubblicato il 21 Settembre 2012 da admin

[:it]

Pablo Picasso

Per sviluppare queste equazioni è indispensabile conoscere bene le operazioni con le frazioni .

Esercizi di base

In questi esercizi ci si deve ricordare la regola empirica ossia se voglio che la x rimanga con coefficiente numerico positivo ed intero (ossia 1) è sufficiente “trasportare” la frazione di sinistra, a destra del simbolo di “=” ma essa CAMBIA DI SEGNO.

Ad esempio:

$x - \cfrac{3}{4}=\cfrac{2}{4}$

$x=\cfrac{2}{4}+\cfrac{3}{4}$

$x=\cfrac{5}{4}$

A.1. $x + \cfrac{5}{6}=\cfrac{8}{6}$	$\left [ \cfrac{1}{2} \right ]$
A.2. $x - \cfrac{1}{4}=\cfrac{3}{4}$	$\left [ 1 ]$
A.3. $x - \cfrac{1}{5}=\cfrac{4}{5}$	$\left [1]$
A.4. $x - \cfrac{3}{2}=\cfrac{5}{2}$	$\left [4]$
A.5. $x - \cfrac{7}{3}=\cfrac{10}{3}$	$\left [ \cfrac{17}{3} \right ]$
A.6. $x - \cfrac{1}{5}=\cfrac{2}{3}$	$\left [ \cfrac{13}{15} \right ]$
A.7. $x + \cfrac{1}{2}=-\cfrac{3}{2}$	$\left [-2]$

In questi esercizi bisogna sommare i coefficienti che moltiplicano la x e poi operare come negli esercizi precedenti.

B.1. $\cfrac{1}{2}x+\cfrac{1}{2}x+\cfrac{5}{6}=\cfrac{8}{6}$	$\left [1]$
B.2. $\cfrac{1}{3}x+\cfrac{2}{3}x-\cfrac{1}{4}=\cfrac{3}{4}$	$\left [ 1 ]$
B.3. $\cfrac{5}{6}x+\cfrac{1}{6}x-\cfrac{1}{5}=\cfrac{4}{5}$	$\left [1]$
B.4. $\cfrac{1}{4}x+\cfrac{3}{4}x-\cfrac{3}{2}=\cfrac{5}{2}$	$\left [4]$
B.5. $\cfrac{2}{5}x+\cfrac{3}{5}x-\cfrac{7}{3}=\cfrac{10}{3}$	$\left [ \cfrac{17}{3} \right ]$
B.6. $\cfrac{1}{5}x+\cfrac{4}{5}x-\cfrac{1}{5}=\cfrac{2}{3}$	$\left [ \cfrac{13}{15} \right ]$
B.7. $\cfrac{4}{7}x+\cfrac{3}{7}x-\cfrac{1}{2}=\cfrac{3}{2}$	$\left [2]$

Negli esercizi successivi, il numero che moltiplica la $x$ deve essere diviso da entrambe le parti ma, essendoci una frazione, è molto più semplice moltiplicare a destra e a sinistra per la frazione che ha come denominatore il numero che moltiplica la x.

Ad esempio

$2x=\cfrac{1}{3}$

La prima cosa che viene da fare è il seguente passaggio:

$\cfrac{2x}{2}=\cfrac{\cfrac{1}{3}}{2}$

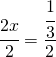
ma la cosa che ritengo più semplice è invece questa:

$\cfrac{1}{2}\cdot 2x=\cfrac{1}{3}\cdot \cfrac{1}{2}$

$\cfrac{1}{\not 2}\cdot \not 2x=\cfrac{1}{6}$

$x=\cfrac{1}{6}$

Seguendo l’esempio precedente, risolvere questi esercizi

C.1. $3x=\cfrac{1}{4}$
C.2. $4x=\cfrac{1}{5}$
C.3. $5x=\cfrac{1}{6}$
C.4. $6x=\cfrac{1}{7}$
C.5. $7x=\cfrac{1}{8}$
C.6. $8x=\cfrac{1}{9}$
C.7. $9x=\cfrac{1}{10}$
C.8. $4x=\cfrac{2}{3}$
C.9. $6x=\cfrac{2}{5}$
C.10. $7x=\cfrac{14}{5}$
C.11. $8x=\cfrac{16}{3}$
C.12. $9x=\cfrac{18}{5}$
C.13. $10x=\cfrac{20}{3}$

Negli esercizi successivi il numero che moltiplica la $x$ è una frazione.

Ad esempio:

$\cfrac{1}{2}x=\cfrac{1}{4}$

In questo caso moltiplico a sinistra ed a destra per il denominatore della frazione che moltiplica la $x$

$2\cdot \cfrac{1}{2}x=\cfrac{1}{4}\cdot 2$

$\not 2\cdot \cfrac{1}{\not 2}x=\cfrac{1}{4}\cdot 2$

$x=\cfrac{1}{2\cdot 2}\cdot 2$

$x=\cfrac{1}{2\cdot \not 2}\cdot \not 2$

$x=\cfrac{1}{2}$

Seguendo l’esempio precedente, risolvere questi esercizi:

D.1. $\cfrac{1}{3}x=\cfrac{1}{4}$
D.2. $\cfrac{1}{4}x=\cfrac{1}{5}$
D.3. $\cfrac{1}{5}x=\cfrac{1}{6}$
D.4. $\cfrac{1}{6}x=\cfrac{1}{7}$
D.5. $\cfrac{1}{7}x=\cfrac{1}{8}$
D.6. $\cfrac{1}{8}x=\cfrac{1}{9}$
D.7. $\cfrac{1}{9}x=\cfrac{1}{10}$
D.8. $\cfrac{1}{4}x=\cfrac{2}{3}$
D.9. $\cfrac{1}{6}x=\cfrac{2}{5}$
D.10. $\cfrac{1}{7}x=\cfrac{14}{5}$
D.11. $\cfrac{1}{8}x=\cfrac{16}{3}$
D.12. $\cfrac{1}{9}x=\cfrac{18}{5}$
D.13. $\cfrac{1}{10}x=\cfrac{20}{3}$

Adesso è necessario fondere gli esercizi del gruppo C con quelli del gruppo D per risolvere gli esercizi successivi.

Ad esempio:

$\cfrac{3}{4}x=\cfrac{5}{7}$

moltiplico a sinistra e a destra per il reciproco del numero che moltiplica la $x$ ossia:

$\cfrac{4}{3}\cdot \cfrac{3}{4}x=\cfrac{5}{7}\cdot \cfrac{4}{3}$

$\cfrac{\not 4}{\not 3}\cdot \cfrac{\not 3}{\not 4}x=\cfrac{5}{7}\cdot \cfrac{4}{3}$

$x=\cfrac{20}{21}$

Seguendo l’esempio precedente, risolvere questi esercizi:

CD.1. $\cfrac{4}{5}x=\cfrac{6}{7}$	$\left [ \cfrac{15}{14} \right ]$
CD.2. $\cfrac{5}{6}x=\cfrac{7}{8}$	$\left [ \cfrac{21}{20} \right ]$
CD.3. $\cfrac{6}{7}x=\cfrac{8}{9}$	$\left [ \cfrac{28}{27} \right ]$
CD.4. $\cfrac{7}{8}x=\cfrac{9}{10}$	$\left [ \cfrac{36}{35} \right ]$
CD.5. $\cfrac{8}{9}x=\cfrac{10}{11}$	$\left [ \cfrac{45}{44} \right ]$
CD.6. $\cfrac{9}{10}x=\cfrac{4}{5}$	$\left [ \cfrac{8}{9} \right ]$
CD.7. $\cfrac{6}{5}x=\cfrac{8}{7}$	$\left [ \cfrac{20}{21} \right ]$
CD.8. $\cfrac{7}{6}x=\cfrac{9}{8}$	$\left [ \cfrac{27}{28} \right ]$

Se si sono risolti gli esercizi precedenti con sicurezza, si possono affrontare questi esercizi.

Per un livello sufficiente [6]:

6.1. $x+\cfrac{1}{2}=-\cfrac{3}{2}$	$\left [ -2 \right ]$
6.2. $\cfrac{2}{3}-x=\cfrac{1}{3}$	$\left [ \cfrac{1}{3} \right ]$
6.3. $-\cfrac{5}{2}x+\cfrac{1}{3}=-\cfrac{3}{2}x+\cfrac{4}{3}$	$\left [ -1 \right ]$
6.4. $\cfrac{2}{5}x-3=-\cfrac{3}{5}x+6$	$\left [ 9 \right ]$
6.5. $\cfrac{1}{2}x+2x+\cfrac{4}{3}=\cfrac{1}{12}+2x$	$\left [-\cfrac{5}{2} \right ]$
6.6. $\cfrac{2}{5}x-\cfrac{3}{5}-\cfrac{1}{3}x=1+\cfrac{1}{5}x-\cfrac{1}{3}-\cfrac{1}{15}$	$\left [-9 \right ]$
6.7. $\cfrac{1}{2}+\cfrac{5}{4}x-\cfrac{1}{8}x+\cfrac{1}{4}=\cfrac{3}{16}x-\cfrac{1}{2}$	$\left [- \cfrac{4}{3} \right ]$

Esercizi per il [7]

7.1. $2x+\cfrac{17-x}{2}=\cfrac{8-3x}{3}+\cfrac{25}{3}$	$\left [ 1 \right ]$
7.2. $x-1-\cfrac{x+3}{2}-3=\cfrac{1-x}{3}$	$\left [ 7 \right ]$
7.3. $\cfrac{x}{2}+3=5-x$	$\left [- \cfrac{4}{3} \right ]$

[:en]

Pablo Picasso

1) $x + \cfrac{1}{2}=-\cfrac{3}{2}$

2) $\cfrac{2}{3}-x=\cfrac{1}{3}$

3) $-\cfrac{5}{2}x+\cfrac{1}{3}=-\cfrac{3}{2}x+\cfrac{4}{3}$

4) $\cfrac{2}{5}x-3=-\cfrac{3}{5}x+6$

5) $\cfrac{1}{2}x+2x+\cfrac{4}{3}=\cfrac{1}{12}+2x$

__________________________________________

6) $\cfrac{2}{5}x-\cfrac{3}{5}-\cfrac{1}{3}x=1+\cfrac{1}{5}x-\cfrac{1}{3}-\cfrac{1}{15}$

7) $\cfrac{1}{2}+\cfrac{5}{4}x-\cfrac{1}{8}x+\cfrac{1}{4}=\cfrac{3}{16}x-\cfrac{1}{2}$

9) $\cfrac{2}{3}x-1+\cfrac{x}{6}=15-x-\cfrac{x}{6}$

10) $\cfrac{1}{2}x-1+2x-3+4x-5=1-\cfrac{1}{2}x$

11) $\cfrac{1}{2}x+3+\cfrac{1+x}{3}=7-x$

12) $x-1-\cfrac{x+3}{2}-3=\cfrac{1-x}{3}$

13) $\cfrac{x}{2}+3=5-x$

14) $5x-1=7-\cfrac{x}{3}$

15) $\cfrac{x}{3}-2=\cfrac{5}{3}+x$

16) $\cfrac{x}{5}+2=\cfrac{1}{5}-x$ [:de]

Pablo Picasso

1) $x + \cfrac{1}{2}=-\cfrac{3}{2}$

2) $\cfrac{2}{3}-x=\cfrac{1}{3}$

3) $-\cfrac{5}{2}x+\cfrac{1}{3}=-\cfrac{3}{2}x+\cfrac{4}{3}$

4) $\cfrac{2}{5}x-3=-\cfrac{3}{5}x+6$

5) $\cfrac{1}{2}x+2x+\cfrac{4}{3}=\cfrac{1}{12}+2x$

__________________________________________

6) $\cfrac{2}{5}x-\cfrac{3}{5}-\cfrac{1}{3}x=1+\cfrac{1}{5}x-\cfrac{1}{3}-\cfrac{1}{15}$

7) $\cfrac{1}{2}+\cfrac{5}{4}x-\cfrac{1}{8}x+\cfrac{1}{4}=\cfrac{3}{16}x-\cfrac{1}{2}$

9) $\cfrac{2}{3}x-1+\cfrac{x}{6}=15-x-\cfrac{x}{6}$

10) $\cfrac{1}{2}x-1+2x-3+4x-5=1-\cfrac{1}{2}x$

11) $\cfrac{1}{2}x+3+\cfrac{1+x}{3}=7-x$

12) $x-1-\cfrac{x+3}{2}-3=\cfrac{1-x}{3}$

13) $\cfrac{x}{2}+3=5-x$

14) $5x-1=7-\cfrac{x}{3}$

15) $\cfrac{x}{3}-2=\cfrac{5}{3}+x$

16) $\cfrac{x}{5}+2=\cfrac{1}{5}-x$ [:]

Pubblicato in Senza categoria | 53 commenti

INVALSI seconda superiore

Pubblicato il 21 Settembre 2012 da admin

Pablo Picasso – 1920

Allego la prova INVALSI dell’anno 2011

matematica-invalsi-2012-seconda-superiore

Pubblicato in Senza categoria | Lascia un commento

Le equazioni di primo grado: esercizi con coefficienti interi

Pubblicato il 21 Settembre 2012 da admin

[:it]

Renè Magritte

Per poterle risolvere sempre ricordarsi che:

moltiplico a sinistra e moltiplico a destra per la stessa quantità
divido a sinistra e divido a destra per la stessa quantità
somma a destra e sommo a sinistra per la stessa quantità

6.1. $7-3x=10$	$[x=-1]$
6.2. $14x-16=12$	$[x=2]$
6.3. $2x-5=7-2x$	$[x=3]$
6.4. $8x-2=11x-8$	$[x=2]$
6.5. $10x+14=10+4x$	$\left [ x=-\cfrac{2}{3} \right ]$
6.6. $4x-15=13-3x$	$[x=4]$
6.7. $x+2x-2=4$	$[x=2]$
6.8. $15x-5x+5=5x+20$	$[x=3]$
6.9. $2=20-4x$	$\left [ x=\cfrac{9}{2} \right ]$
6.10. $x+2-3x=3+x-7x+5$	$\left [ x=\cfrac{3}{2} \right ]$
6.11. $2x-3+3x=5-x+4$	$[x=2]$
6.12. $2x-4+x+3=5-2x+x+6$
6.13. $-8x+2+5x=7-4x$
6.14. $2+x+3-4x=6+x+7$
6.15. $x+3-3x=5-x+1$
6.16. $4(10-2x)=3(x-5)$
6.17. $3(x-1)=2(1-x)$
6.18. $2x-3x-5=4+3x$
6.19. $7-3x+7x=6x-3$
6.20. $12x-5x-3=5-3x$
6.21. $2(x-1)=3(x-3)$

Prerequisiti:

somme e moltiplicazione tra numero e binomio, tra binomi

[:en]

Renè Magritte

Per poterle risolvere sempre ricordarsi che:

moltiplico a sinistra e moltiplico a destra per la stessa quantità
divido a sinistra e divido a destra per la stessa quantità
somma a destra e sommo a sinistra per la stessa quantità

6.1. $7-3x=10$	$[x=-1]$
6.2. $14x-16=12$	$[x=2]$
6.3. $2x-5=7-2x$	$[x=3]$
6.4. $8x-2=11x-8$	$[x=2]$
6.5. $10x+14=10+4x$	$\left [ x=-\cfrac{2}{3} \right ]$
6.6. $4x-15=13-3x$	$[x=4]$
6.7. $x+2x-2=4$	$[x=6]$
6.8. $15x-5x+5=5x+20$	$[x=3]$
6.9. $2=20-4x$	$\left [ x=\cfrac{9}{2} \right ]$
6.10. $x+2-3x=3+x-7x+5$	$\left [ x=\cfrac{3}{2} \right ]$
6.11. $2x-3+3x=5-x+4$	$[x=2]$
6.12. $2x-4+x+3=5-2x+x+6$
6.13. $-8x+2+5x=7-4x$
6.14. $2+x+3-4x=6+x+7$
6.15. $x+3-3x=5-x+1$
6.16. $4(10-2x)=3(x-5)$
6.17. $3(x-1)=2(1-x)$

Prerequisiti:

somme e moltiplicazione tra numero e binomio, tra binomi

[:de]

Renè Magritte

Per poterle risolvere sempre ricordarsi che:

moltiplico a sinistra e moltiplico a destra per la stessa quantità
divido a sinistra e divido a destra per la stessa quantità
somma a destra e sommo a sinistra per la stessa quantità

6.1. $7-3x=10$	$[x=-1]$
6.2. $14x-16=12$	$[x=2]$
6.3. $2x-5=7-2x$	$[x=3]$
6.4. $8x-2=11x-8$	$[x=2]$
6.5. $10x+14=10+4x$	$\left [ x=-\cfrac{2}{3} \right ]$
6.6. $4x-15=13-3x$	$[x=4]$
6.7. $x+2x-2=4$	$[x=6]$
6.8. $15x-5x+5=5x+20$	$[x=3]$
6.9. $2=20-4x$	$\left [ x=\cfrac{9}{2} \right ]$
6.10. $x+2-3x=3+x-7x+5$	$\left [ x=\cfrac{3}{2} \right ]$
6.11. $2x-3+3x=5-x+4$	$[x=2]$
6.12. $2x-4+x+3=5-2x+x+6$
6.13. $-8x+2+5x=7-4x$
6.14. $2+x+3-4x=6+x+7$
6.15. $x+3-3x=5-x+1$
6.16. $4(10-2x)=3(x-5)$
6.17. $3(x-1)=2(1-x)$

Prerequisiti:

somme e moltiplicazione tra numero e binomio, tra binomi

[:]

Pubblicato in Senza categoria | 68 commenti

Esercizi su nomenclatura e ulteriori definizioni sui database

Pubblicato il 2 Settembre 2012 da admin

In un sistema informatico quali tra questi sono componenti software?

A – archivi

B – strumentazione

C – applicazioni

D – supporti fisici

2 Che cosa significa l’acronimo EDP?

A – Electronic Data Program.

B – Electronic Disk Processing

C – Electonic Data Processing

D – Electronic Disk Program

3 – Quali delle seguenti affermazioni sui database sono vere?

A – un database è una specie di memoria digitale intelligente

B – un database permette di migliorare la compressione dei dati

C – nei database la definizione dei dati e i dati sono salvati all’interno dello stesso database

D – in un database è possibile integrare i programmi con i dati

4 – Per quali dei seguenti scopi può essere utilizzato un database?

A – per la scrittura di un documento lungo e strutturato come un libro

B – per gestire i propri contatti

C – per la gestione di una biblioteca

D – per migliorare le prestazioni di un computer

5 – Qual è il più importante vantaggio dei DB?

A – l’applicazione e i suoi dati sono indipendenti

B – i dati occupano meno spazio su disco

C – i DBMS gestiscono più velocemente i dati

D – facilitano la duplicazione dei file

6 – Che cosa significa DBMS

A – Database Management Software

B – Database Mirroring System

C – Database Multiuser System

D – Database Management System

Test Vero/Falso

1 – In un database l’applicazione e i suoi dati sono indipendenti l’uno dall’altro

2 – I database risolvono i problemi di inconsistenza causati dall’incongruenza dei dati

Pubblicato in Uncategorized | Lascia un commento

2.1. Nomenclatura e ulteriori definizioni sui database

Pubblicato il 2 Settembre 2012 da admin

Vasilij Kandinski

Spesso si parla di sistema informativo e sistema informatico come se fossero un unicum; è corretto distinguerli.

Per sistema informativo si intende l’insieme di strumenti automatici, procedure manuali, risorse umane e materiali, norme organizzative, orientato alla gestione delle informazioni.

Per sistema informatico (EDP = Electronic Data Processing) è un sottoinsieme del sistema informativo che si dedica solo alla gestione automatica delle informazioni.

Il sistema informativo è composto da: archivi e applicazioni che formano il software, e supporti fisici e strumentazione che formano i componenti dell’hardware.

Per rafforzare l’importanza dei database si pensi sempre alla gestione del magazzino. Mentre una persona sta aggiornando le scorte, nel negozio si continua a vendere la merce. Entrambe le persone devono accedere al file che gestisce il magazzino ma non possono accedervi contemporaneamente in quanto per leggere o scrivere un file bisogna dire al sistema che in quel momento ho aperto il file.

Ad esempio si provi a condividere un file di word da un disco di rete. (Si intende uno spazio di memoria condiviso da più PC), il messaggio che compare è ce se si vuole fare una copia del file si può fare ma poi quando si va a salvarlo cosa succede all’altra copia che sta venendo usata dall’altra persona?

Si generano i seguenti problemi:

– incongruenza: il pezzo si troverebbe in quantitativi diversi rispetto al file che tiene questa informazione

– inconsistenza: il dato non ha più significato diventando inutilizzabile

– ripetizione del dato: il dato viene ripetuto in moltissimi file che utilizzano quel quantitativo

Un database per essere definito in maniera corretta dovrebbe rispettare sempre i seguenti vincoli:

1 – indipendenza dalla struttura fisica dei dati: ossia cambiare i supporti di memoria su cui vengono scritti i dati non devono inficiare la struttura

2- indipendenza logica: se devo aggiungere una caratteristica al pezzo di magazzino ad esempio le sue dimensioni, il programma che estrae il quantitativo deve continuare a funzionare anche se è stato aggiunta una nuova descrizione

DBMS

Database Management System

Il programma che evita i dati ripetuti, l’incongruenza, l’inconsistenza è il DBMS.

Il suo compito è:

gestione di grandi moli di dati: si evitano i dati ridondanti ossia le ripetizioni

condivisione: lo stesso dato viene condiviso da molti utenti senza che per questo rimangano dati non veritieri; ad esempio nel caso dell’aggiornamento del magazzino e della vendita del pezzo, il DBMS riesce a mantenere sempre il quantitativo corretto del pezzo con opportuni meccanismi di gestione delle collisioni.

persistenza: controllo agli accessi dei dati mediante opportune regole di sicurezza, ad esempio non si vuole che il commesso possa cambiare il prezzo della merce ma solo il responsabile del reparto, entrambi possono accedere al dato ma solo uno dei due può modificarlo.

Maggiori DBMS attualmente in commercio:

– Oracle

–MS SQL server

– MS Access

– Sybase

– Informix

– Ingres

– MySQL

– PostgreSQL

Che differenza intercorre tra Database e DBMS?

In letteratura non si fa distinzione ma in fase didattica per Database intendo la struttura dei dati opportunamente organizzata, mentre per DBMS intendo quel software che garantisce la grande quantità dei dati, la condivisione e la persistenza dei dati.

Pubblicato in Senza categoria | Lascia un commento

2 – Introduzione ai database

Pubblicato il 2 Settembre 2012 da admin

Giacomo Balla

I database sono l’evoluzione naturale della gestione dei file. Ai primi programmatori la cosa più importante era far ripetere le operazioni che, altrimenti , se fatte a mano avrebbe portato via moltissimo tempo e risorse.

Si pensi immediatamente, ad esempio, al calcolo di un’area o di un percorso: tale operazione viene effettuate mediante uno o più integrali. Ebbene tale operazione adesso viene effettuata mediante l’utilizzo di opportuni algoritmi implementati attraverso degli ottimi software.

Una volta terminato un calcolo, a volte, è necessario salvarlo in qualche parte, per rielaboralo successivamente o semplicemente per poi sommarlo a dei calcoli intermedi.

Ad esempio il semplice problema di sapere la media dei promossi al termine di un anno scolastico richiede il salvataggio del dato alla fine di ogni scrutinio per poi essere sommato complessivamente al termine di tutte le operazioni di fine anno.

A questa esigenza si è poi affiancata un’altra ossia quella di memorizzare tutto un insieme di informazioni che non fossero solo di carattere numerico ma anche di formato testo.

Un qualunque corso di programmazione che si rispetti tratta sempre la gestione dei file come si aprono, come si chiudono, come si possono leggere. Sempre più però tale trattazione rimane relegata a chi poi gestirà file più che alla programmazione in generale.

Infatti adesso si cerca di concentrarsi sulla gestione dei dati a largo spettro.

Un esempio prima di tutto:

la gestione un magazzino richiede la quantità di una merce, almeno la sua descrizione.

Un database DEVE seguire le seguenti regole:

1 – semplice: le informazioni devono essere ottimizzate rispetto al tempo e allo spazio

2 – efficiente: l’utilizzo delle risorse deve essere ottimizzato rispetto al tempo e allo spazio – efficiente utilizzo del processore e utilizzo della memoria.

3 – efficace: nel senso che le informazioni devono essere rappresentative della realtà che si vuole analizzare

4 – sicuro: le operazioni sui dati sono permesse solo a utenti autorizzati

5- solido: deve resistere a disfunzioni ed errori, come guasti al computer o alla rete oppure all’erore di un operatore che chiede un dato inesistente

6- condiviso: deve permettere a più utenti di accedere contemporaneamente ai dati.

Pubblicato in Senza categoria | Contrassegnato algoritmi, giacomo balla | Lascia un commento

Indice di informatica

Pubblicato il 2 Settembre 2012 da admin

LA PROGRAMMAZIONE

1.– La creazione di un algoritmo – programmazione top-down

1.2.– La ricorsione

1.3. Esercizio sulla ricorsione

DATABASE

2. Introduzione ai database

2.1. Nomenclatura e ulteriori definizioni sui database

2.1.1. Esercizi su nomenclatura e ulteriori definizioni di database

2.2- Modellazione dei dati

2.3- Modelli logici

2.4. Modello gerarchico

2.5. Modello reticolare

Appendice

A1. Verifica: gruppo 1

A2. Verifica: gruppo 2.

A3. Verifica: gruppo 3.

SQL

3.1. introduzione all’SQL

3.2. Select: i primi passi

3.3. Select: criteri di ricerca

SISTEMI DI NUMERAZIONE

4.1. Dalla Base 2 alla base 5

4.2. Dalla base 5 alle altre basi

4.3. Sistema additivo: i romani

4.4. Differenza tra sistema additivo e sistema posizionale

Appendice – esercitazioni

A.1- sui cicli

A.1.1. Soluzione

A.2- passaggi di base

A.2.1. Soluzione gruppo A

A.2.2. Soluzione gruppo B

A.2.3. Soluzioni gruppo C

A.3. La ricorsione

A.4. Verifichiamo l’ABC: stampa a video, semplici cicli

Pubblicato in Senza categoria | Lascia un commento

1 – La creazione di un algoritmo – programmazione top-down

Pubblicato il 2 Settembre 2012 da admin

Paul Cézanne

Algoritmo = è l’adattamento del nome Al-Khwarizmi alla lingua latina. Al-Khwarizmi visse a Bagdad nell’800 d.C., fu il matematico che riuscì a raccogliere la maggior parte degli scritti dell’epoca nell’ambito scientifico studiandoli e riportando, ad esempio, le conclusioni geometriche dei greci per la risoluzione delle equazioni di secondo grado. Grazie ai numerosi scambi commerciali del mediterraneo la matematica trovò terreno molto fertile in Italia con matematici del calibro di Leonardo Pisano, Scipione Dal Ferro, Niccolò Tartaglia, Gerolamo Cardano, Ludovico Ferrari e Rafael Bombelli.

Top-down: letteralmente dall’alto verso il basso.

Fare un buon programma significa fare una buona analisi, poi il procedimento attraverso il quale esso si realizza in un programma richiede solo delle conoscenze tecniche dei vari linguaggi di programmazione.

Quando si deve affrontare un programma si deve cercare di atomizzare le istruzioni ossia creare piccoli pezzi che possono essere riutilizzati anche per altri programmi.

La programmazione top – down parte dal fatto che si debba suddividere i problemi in tanti piccoli problemi facilmente realizzabili.

Ad esempio: andare ad acquistare un nuovo portatile.

La programmazione top – down ci porta ad operare in questi termini:

1- uscire

2- se è distante il negozio prendere l’automobile altrimenti andare a piedi

3- entrati in negozio chiedere dove è il reparto dei computer portatili

4 …

Come si può osservare tale fatto implica la suddivisione di grossi problemi in piccoli problemi.

L’utilizzo delle procedure all’interno di un programma permette appunto la suddivisione dei problemi in piccoli problemi.

Pubblicato in Senza categoria | Contrassegnato algoritmo, Pittori: Paul Cézanne, top down | Lascia un commento

TFA – Padova – Agosto 2012

Pubblicato il 29 Agosto 2012 da admin

Joan Mirò

Allego la prova del secondo scritto della sessione 2012 per il TFA.

Tale prova è stata creata dall’Università di Padova. Si notino come gli esercizi siano improntati strettamente per i soli laureati in matematica escludendo di fatto le altre lauree pur potendo accedere a tale classe di concorso.

Si nota come gli esercizi non trattino assolutamente gli argomenti usati in un normale corso di matematica di alcuna scuola italiana.

Se la scuola italiana affrontasse tali argomenti sicuramente avremo persone molto più preparate ad affrontare l’Università ma poi bisogna vedere se il mondo del lavoro è in grado di valorizzare tali competenze!

TFA Padova agosto 2012

Pubblicato in Senza categoria | Contrassegnato TFA | Lascia un commento

Per ripassare un intero anno

Pubblicato il 29 Giugno 2012 da admin

Filippo Tommaso Marinetti

Espressioni con numeri interi:

1. $\left\{ \left [2-7\cdot\left(4-6\right )\right]:\left(-2 \right)-\left (-2^{3}+2^{2}\right)\right\}:\left(-2\right)+\left[-\left(-2+7\right)\cdot\left(-4\right)\right]$

2. $\left [ \left ( 6-22 \right ):\left ( -2 \right )^{3}+\left ( 11-13 \right )\cdot \left ( -7+4 \right ) \right ]\cdot \left ( 8-11 \right )+\left(-2\cdot3+4\cdot9\right)$

3. $\left ( -4+2 \right )^{3}\cdot 4-\left \{ \left [ \left ( 5-7 \right )\cdot \left ( 4-1 \right )+3\right ]:3-\left ( -5 \right )+2\left ( -4 \right ) \right \}$

4. $\left \{ -\left ( +7 \right )-\left [ -3\left ( -3 \right ) \right ] \right \}+\left \{ \left [ -6\cdot \left ( -1 \right ) \right ]-\left [ -\left ( -2 \right ) \right ] \right \}-\left \{ -\left [ -\left ( -5 \right ) \right ]-\left [ \left ( -1 \right )\cdot \left ( -3 \right ) \right ] \right \}$

5. $\left ( 3\cdot 5-40:2 \right )-\left \{ 5\cdot 2-\left [ 3\cdot \left ( -2 \right )-\left ( -15 \right ):3 \right ]+\left [ \left ( -12 \right ):\left ( -3 \right )-\left ( -6 \right )\cdot \left ( -2 \right ) \right ] \right \}:\left [ \left (-5\right )\cdot 4+17 \right ]$

6. $\left \{ +12-\left [ +2+2^{3}:\left ( -2 \right )^{2}\cdot \left ( 2^{4}:2^{3} \right )^{2} \right ]:\left [ \left ( -2^{2} \right )^{2}:2^{3} \right ] \right \}\cdot 3+\left ( -3 \right )^{3}$

7. $\left ( 2^{2} \right )^{5}\cdot \left ( -2 \right )^{3}:\left \{ \left [ -\left ( -2 \right )^{2} \right ]^{3}\cdot \left [ -\left ( -2 \right )^{2} \right ]^{2} \right \}\cdot \left ( -2^{2} \right ):\left ( -2 \right )^{4}$

8. $\left \{ \left [ -\left ( -3 \right )^{3} \right ]^{5}\cdot \left [ \left ( -3 \right )^{5} \right ]^{2} \right \}:\left \{ -\left ( -3 \right )^{3}\cdot \left ( -3 \right )^{7}\cdot \left [ \left ( -3 \right )^{2} \right ]^{7} \right \}+3^{0}$

La rappresentazione dei numeri razionali su una retta

Rappresenta su una retta orientata le seguenti frazioni, indicando per ogni frazione se è propria, impropria o apparente

9. $\cfrac{1}{2};\cfrac{3}{4};\cfrac{1}{3};-\cfrac{1}{2};\cfrac{8}{5};\cfrac{7}{8}$

10. $-\cfrac{5}{6};\cfrac{3}{2};\cfrac{5}{4};-\cfrac{8}{9};\cfrac{3}{3};\cfrac{9}{5}$

11. $-\cfrac{4}{3};\cfrac{5}{2};-\cfrac{11}{6};-\cfrac{7}{2};\cfrac{7}{6};\cfrac{5}{4}$

Le espressioni contenenti somme algebriche
Calcola il valore delle seguenti espressioni

12. $7-\left [ \left ( 3+\cfrac{1}{5}-\cfrac{3}{4}-2 \right )-\left ( \cfrac{2}{5}-6 +\cfrac{3}{4}-\cfrac{1}{2}\right )\right ]+\cfrac{6}{5}-\left ( \cfrac{7}{20}+\cfrac{1}{20} \right )$

13. $\cfrac{1}{9}-\cfrac{1}{12}+\left ( \cfrac{1}{8}-\cfrac{23}{9}\right )-\left [ \cfrac{3}{8}+\left ( \cfrac{1}{3}-\cfrac{5}{2} \right )-\cfrac{1}{6} \right ]+\cfrac{4}{9}$

14. $4-\left [ 2+\left ( 1-\cfrac{2}{3} \right )-\left ( -4+\cfrac{1}{5} \right ) \right ]+\left [ 7-\left ( 6+\cfrac{1}{15}\right )-\cfrac{2}{5} \right ]$

Pubblicato in Senza categoria | Lascia un commento

Equazioni di primo grado a coefficienti frazionari

INVALSI seconda superiore

Le equazioni di primo grado: esercizi con coefficienti interi

Esercizi su nomenclatura e ulteriori definizioni sui database

2.1. Nomenclatura e ulteriori definizioni sui database

2 – Introduzione ai database

Indice di informatica

1 – La creazione di un algoritmo – programmazione top-down

TFA – Padova – Agosto 2012

Per ripassare un intero anno

Registrazione

Categorie

Articoli recenti

Commenti recenti

Meta

Categorie

Articoli recenti

Commenti recenti

Meta

Whymatematica