
Sergey Tyukanov
[WpProQuiz 8]


Sergey Tyukanov
[WpProQuiz 8]
 [WpProQuiz 7]
[WpProQuiz 7]
 [WpProQuiz 6]
[WpProQuiz 6]

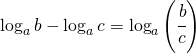
Esempi sulle precedenti proprietà
 Determinare il massimo ed il minimo assoluti della funzione:
Determinare il massimo ed il minimo assoluti della funzione:![]()
nell’intervallo chiuso
![]()
soluzione
2. Determinare il massimo ed il minimo assoluti della funzione
![]()
nell’intervallo
![Rendered by QuickLaTeX.com \left [ -2;-\cfrac{1}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f1673929900f5e8c9a8d7064997636d4_l3.png)
soluzione
3. Determinare il massimo ed il minimo assoluti della funzione:
![]()
nell’intervallo:
![]()
soluzione
 [WpProQuiz 5]
[WpProQuiz 5]
Data la funzione:
![]()
a) calcola a e b sapendo che il suo grafico passa per l’origine e interseca la retta di equazione y=4 nel punto di ascissa 3.
b) rappresenta il grafico di f(x) per i valori di a e b trovati
c) risolvi analiticamente e graficamente la disequazione:
![]()
Sviluppo.
a) Passando per l’origine deve essere soddisfatta la
(1) ![]()
e affermare che interseca una retta in un particolare punto significa che quel punto appartiene alla curva per cui deve valere anche questa relazione:
(2) ![]()
analizzando la (1)
![]()
perché se così non fosse la funzione di partenza degenerebbe in un punto coincidente con l’origine.
Risolvo l’equazione:
![]()
che equivale a scrivere (partendo dalla definizione stessa di logaritmo)
![]()
che fornisce il valore
![]() .
.
Sostituendo adesso il valore trovato nella (2) si deve risolvere l’equazione:
![]()
ma
![]() .
.
![]() .
.
![]() .
.
la funzione di partenza diventa:
![]()
b) Per rappresentare la funzione
![]()
posso non utilizzare le conoscenze della derivata per la sua rappresentazione partendo dal grafico della funzione
![]()
che è:
![]() ” width=”1341″ height=”1034″ />
” width=”1341″ height=”1034″ />
La moltiplicazione per 2 fa sì soltanto che sia un po’ più alta (si noti la linea rossa) e che tenda meno velocemente allo 0.
![]()
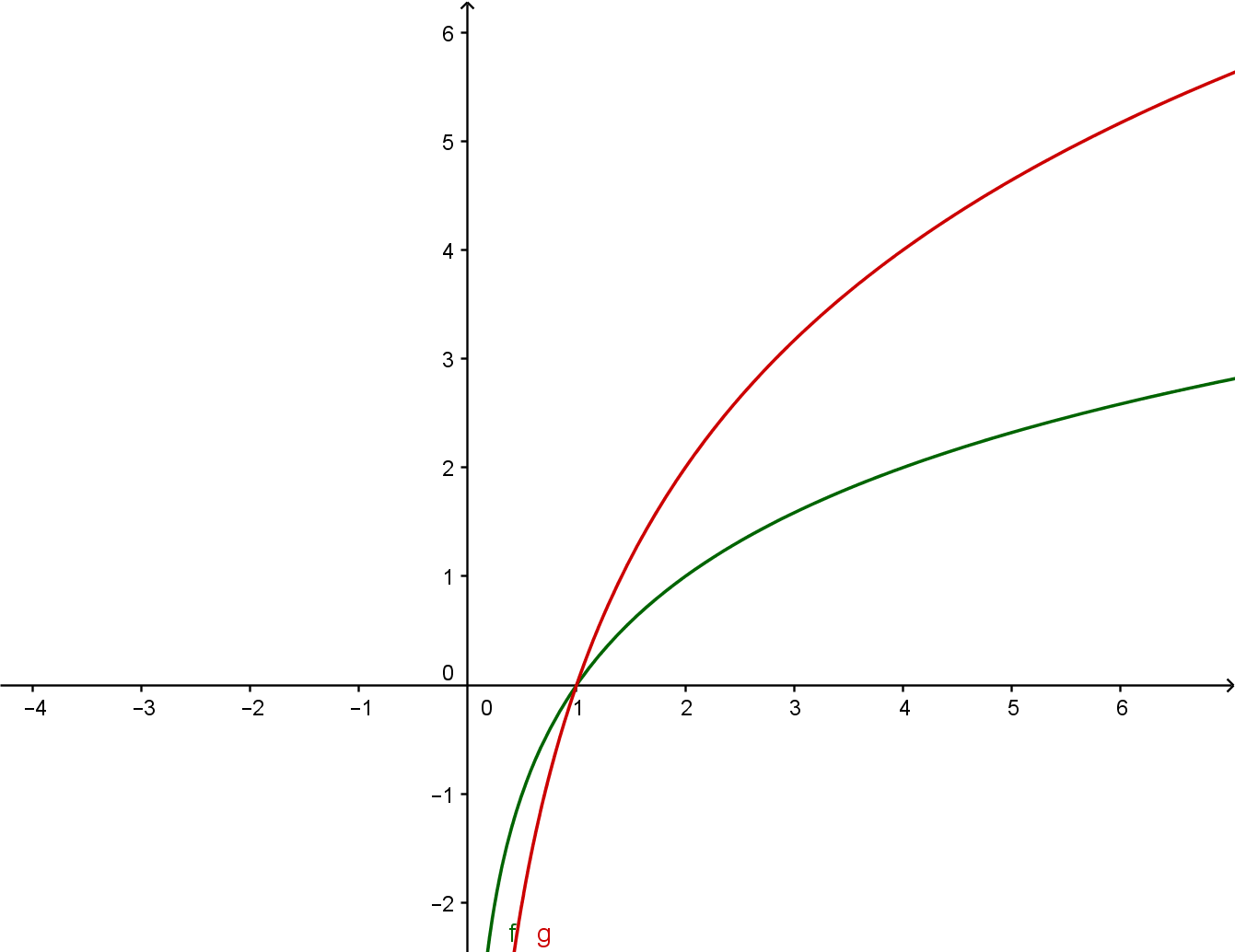
sommare 1 all’argomento della radice significa traslare all’indietro il grafico (linea blu identificata con la lettera h) con asintoto in x=-1
![]()
c) Risolvo adesso analiticamente la disequazione:
![]() .
.
![]()
che diventa:
![]() .
.
il dominio è dato dallo studio del sistema di disequazione fornito dagli argomenti dei due logaritmi ossia:
![]()
che mi dà come soluzione
![]()
torno alla disequazione che diventa:
![]() .
.
![]()
Avendo la stessa base ed essendo questa maggiore di 1 posso studiare la disequazione:
![]() .
.
![]()
Risolvo l’equazione associata:
![]() .
.
per risolvere la disequazione di secondo grado uso il metodo della parabola ossia:
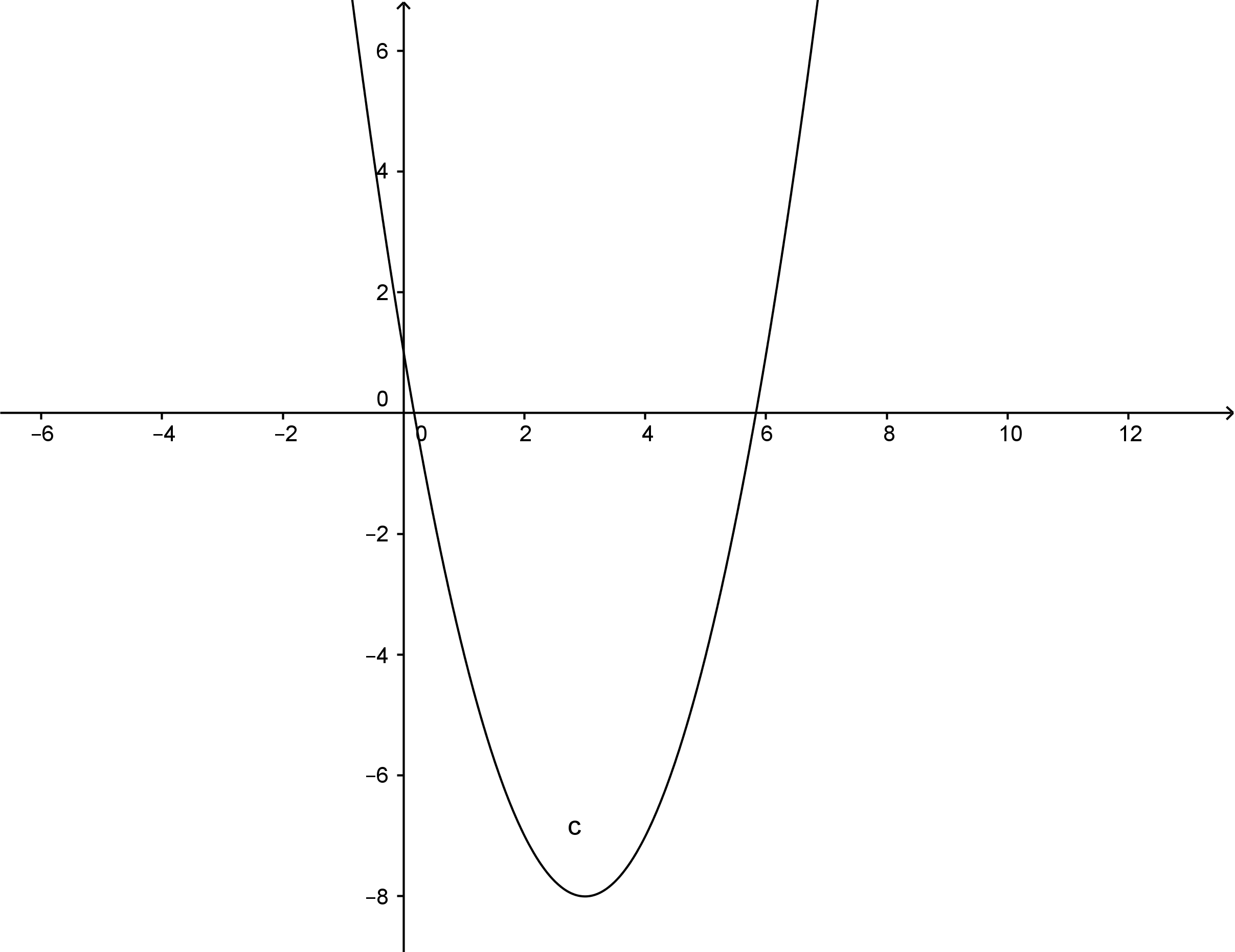 i punti d’intersezione con l’asse x sono le soluzioni precedentemente trovate.
i punti d’intersezione con l’asse x sono le soluzioni precedentemente trovate.
I valori per cui la parabola è maggiore di zero sono i valori esterni ma ricordandomi anche il dominio che era:
![]()
la soluzione della disequazione diventa:
![]()
e
![]() .
.
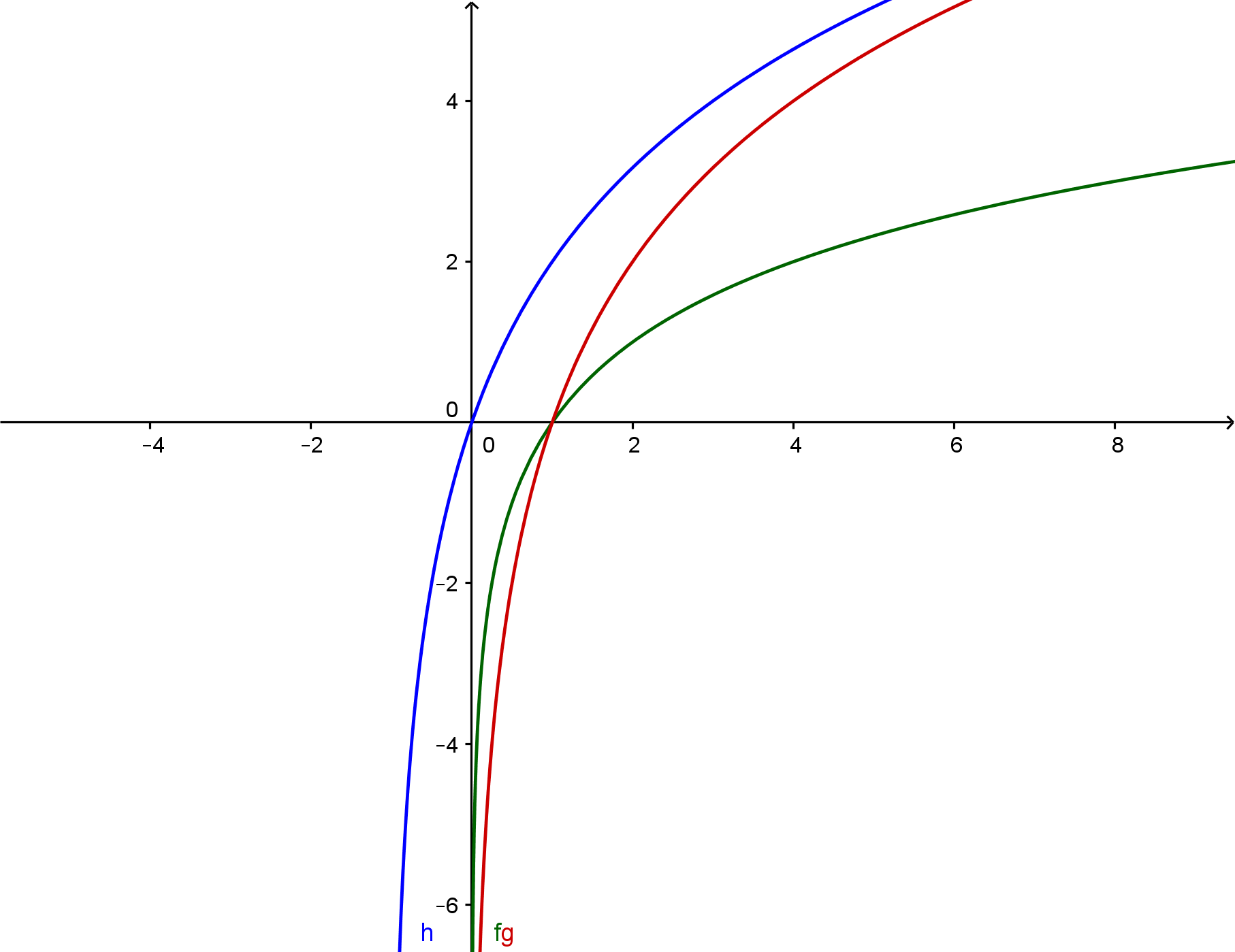
Per risolverla graficamente studio le seguenti due funzioni:
![]()
identificata con la linea rossa
e al funzione:
![]()
identificata con la linea blu.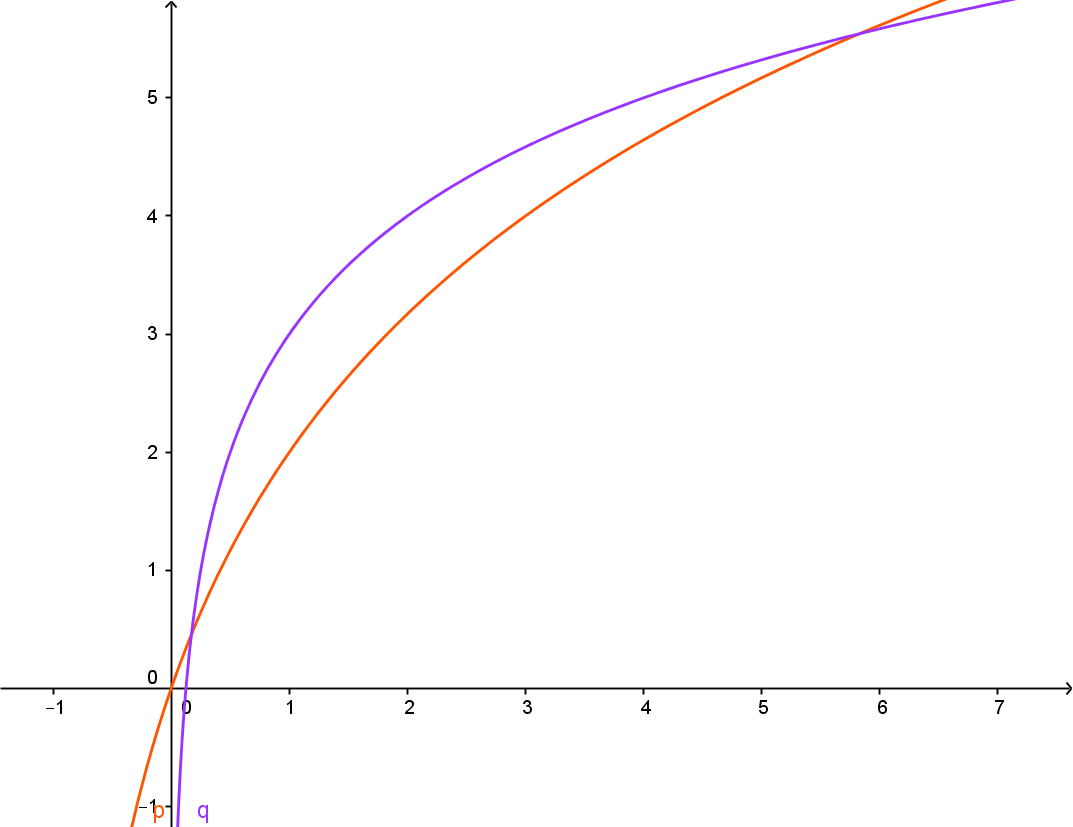 si nota infatti che la linea rossa è sopra a quella blu per i valori precedentemente trovati analiticamente.
si nota infatti che la linea rossa è sopra a quella blu per i valori precedentemente trovati analiticamente.
![]()
Per risolverla devo avere la stessa base
Per fare questo utilizzo la seguente proprietà:
![]()
ossia:
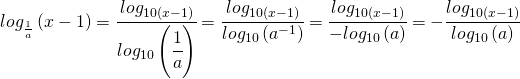
e
![]()
e inserendoli in quella di partenza ho:
![]()
e quindi facendo il m.c.m. la disequazione i di partenza diventa:
![]()
la disequazione di partenza è diventata:
![]()
Lo studio del dominio parte dall’argomento del logaritmo posto al numeratore:
![]()
ossia
![]()
il dominio diventa:
![]()
Adesso studio il segno del numeratore e del denominatore.
Il denominatore:
![]() >0
>0
E’ positivo per
![]()
Mentre è negativo per
![]()
Il numeratore:
![]()
il -3 viene rappresentato con una linea tratteggiata.
![]() e quindi diventa
e quindi diventa
![]()
Concentrandosi solo sugli argomenti devo risolvere la seguente semplice disequazione:
![]()
quindi
![]()
Ho la seguente rappresentazione grafica:
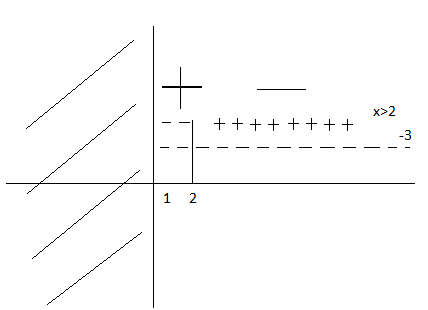
Adesso unisco il denominatore, che mi fornisce la dipendenza della disequazione dal parametro, ed il segno del numeratore.
Per
![]() il denominatore è positivo per cui ho il seguente schema:
il denominatore è positivo per cui ho il seguente schema:
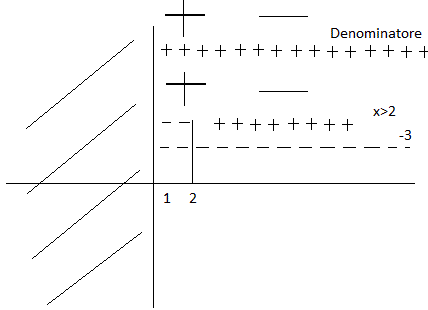
e quindi la prima soluzione è:
Per ![]()
![]()
Per ![]() il denominatore è negativo ed ho il seguente schema:
il denominatore è negativo ed ho il seguente schema:
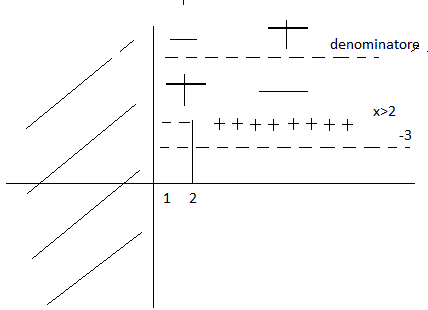
ed ho la seconda soluzione:
Per ![]()
![]()
Per affrontare con sicurezza questa parte dell’INVALSI è necessario avere queste competenze:
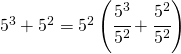
![]()
Ad esempio:
![]()
Ad esempio

Igor Morski
Quale metodo usare per risolvere i sistemi d’equazione nel minor tempo possibile e in maniera corretta?
Qui inserisco una serie di esercizi e nelle soluzioni inserisco il metodo che io ritengo migliore ma non necessariamente quello che tutti possono ritenere migliore. Alla fine uno può trovarsi meglio aver usato un metodo invece che un altro.
Esercizi facili per prendere la mano (6)
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
![Rendered by QuickLaTeX.com \left [ \left ( 1,\cfrac{3}{2} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-bc1069d7f684e3b18c1030db0db3c4be_l3.png) |
| 6.7. |
Esercizi più complessi (7)
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
7.4. 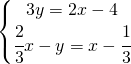 |
![Rendered by QuickLaTeX.com \left [ \left ( \cfrac{5}{3},-\cfrac{2}{9} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-97bb486ade1c64964c37a04a3fde6c30_l3.png) |
7.5. 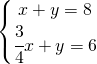 |
|
7.6. 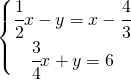 |
Verso un buon livello (8)
8.1. 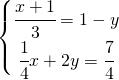 |
|
Verso il l’ottimo (9)
9.1. 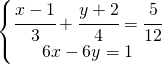 |
![Rendered by QuickLaTeX.com \left [ \left (\cfrac{1}{2},\cfrac{1}{3} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-801c5aa12d2b23cdf869d61901284917_l3.png) |
L’ottimo (10)
10.1. 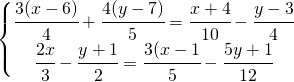 |
|