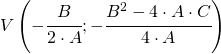[:it]
Rappresentare sul piano cartesiano la parabola di equazione
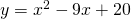
1 punto: intersezioni con gli assi
calcolo dell’intersezione.
Pongo la x=0 ed ho
y=20.
Adesso pongo la y=0 e devo risolvere l’equazione di secondo grado:
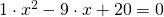
identifico la A, la B e la C ossia i tre coefficienti che mi permettono di risolvere l’equazione di secondo grado.
A= 1
B= -9
C=20
Li sostituisco nella:
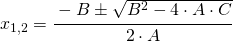
e viene:
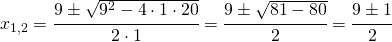
ho le seguenti intersezioni:
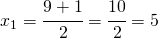
e
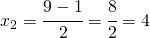
2 punto: analisi del segno di A
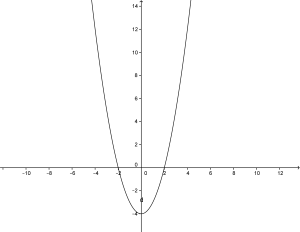
la A=1 quindi la parabola ha la concavità verso l’alto ossia è così fatta:
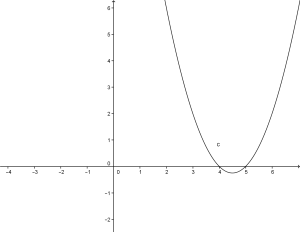
3 punto: coordinate del vertice
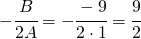
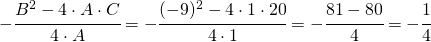
[:en]Rappresentare sul piano cartesiano la parabola di equazione
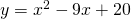
1 punto: intersezioni con gli assi
calcolo dell’intersezione.
Pongo la x=0 ed ho
y=20.
Adesso pongo la y=0 e devo risolvere l’equazione di secondo grado:
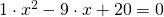
identifico la A, la B e la C ossia i tre coefficienti che mi permettono di risolvere l’equazione di secondo grado.
A= 1
B= -9
C=20
Li sostituisco nella:
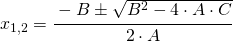
e viene:
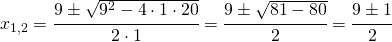
ho le seguenti intersezioni:
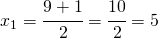
e
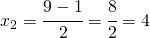
2 punto: analisi del segno di A
la A=1 quindi la parabola ha la concavità verso l’alto ossia è così fatta:
3 punto: coordinate del vertice
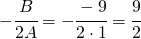
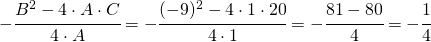
(versione tedesca)[:de]
Jim Warren
Stelle diejenige Parabel auf dem Koordinatensystem dar:
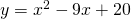
Punkt 1: Interasektion der Axen
Rechnung der Intersektionen
Stelle x=0 und man erhält
y=20.
Jetzt stelle ich y=0 und muss die Gleichung des zweiten Grades lösen
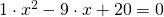
Ich identifiziere A,B und C als drei Koefitienten, die mir die Möglichkeit geben die Gleichung des zweiten Grades zu lösen.
A= 1
B= -9
C=20
Ích ersetze sie:
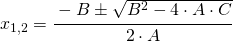
und man hat:
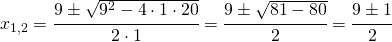
man hat die folgenden Intersektionen:
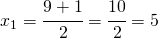
und
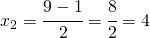
Punkt 2: Analyse des Zeichens A
Das A=1, also die Parabel hat Höhlung von unten nach oben; und wird so dargestellt:
Punkt 3: Koordinaten des Scheitelpunktes der Parabel:
[:]
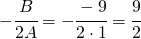
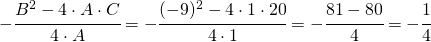[WpProQuiz 2]
