SCIENZE E TECNOLOGIE INFORMATICHE

Verifica finale di Excel

Pubblicato il 16 Maggio 2017 da admin

Marion Adams

Completare tutti gli esercizi presenti in questo file excel ed inviarlo, al termine dei lavori a francesco.bragadin@whymatematica.com

Verifica finale

Pubblicato in Senza categoria | Lascia un commento

[:it]Geometria nello spazio: esercizio 1[:]

Pubblicato il 13 Maggio 2017 da admin

[:it]

Guido Borelli

Data la sfera di centro $C(2,-3,0)$ e raggio 2 determinare le equazioni dei due piani tangenti e paralleli al piano $3x-y+z=0$

Svolgimento

Essendo piano paralleli al piano dato soddisferanno alla relazione

$\cfrac{3}{a}=-\cfrac{1}{b}=\cfrac{1}{c}$

$a=-3b$

$c=-b$

L’equazione del piano diventa:

$-3bx+by-bz+d=0$

Adesso pongo la distanza tra il centro della sfera e i piani uguale alla lunghezza del raggio

$r=\cfrac{\left |ac_^{x}+bc_{y}+cc_{z}+d \right |}{\sqrt{a^{2}+b^{2}+c^{2}}}$

sostituendo adesso i valori numerici si ha:

$r=\cfrac{\left |-3b\cdot 2-3b+d \right |}{\sqrt{9b^{2}+b^{2}+b^{2}}}=2$

$r=\cfrac{\left |-9b+d \right |}{\sqrt{11b^{2}}}=2$

Essendovi il modulo avrò le seguenti due equazioni

$-9b+d=2b\sqrt{11}$ che ha come soluzione

$d=b(2\sqrt{11}+9)$

$9b-d=2b\sqrt{11}$

$d=b(-2\sqrt{11}+9)$

Le equazioni dei piani sono quindi:

$-3x+y-z+2\sqrt{11}+9=0$

$-3x+y-z-2\sqrt{11}+9=0$

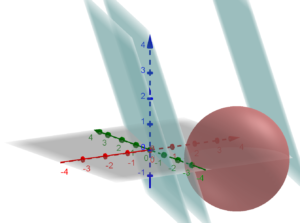
Graficamente si ha:

[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Geometria nello spazio: esercizio 3[:]

Pubblicato il 13 Maggio 2017 da admin

[:it]

Paul Klee

Data la retta di equazione:

$\left\{\begin{matrix} x=t\\ y=2t\\ z=t \end{matrix}\right.$

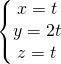
e la retta di equazione:

$\left\{\begin{matrix} x+y+z-3=0\\ 2x-y=0 \end{matrix}\right.$

ed il punto $P(1,0,-2)$

determinare l’equazione del piano passante per P e parallelo alle due rette.

Svolgimento

Perché esista tale piano le due rette devono essere complanari ed affinché che tale condizione sia soddisfatta è necessario che si intersechino in un punto.

E’ sufficiente determinare il valore di t sostituendo le coordinate nella seconda retta:

$\left\{\begin{matrix} t+2t+t-3=0\\ 2t-2ty=0 \end{matrix}\right.$

$t=\cfrac{3}{4}$

ed il punto di intersezione esiste e vale:

$T\left ( \cfrac{3}{4},\cfrac{3}{2},\cfrac{3}{4} \right )$

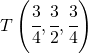
Adesso trovando il piano che contiene le due rette posso determinare poi quello parallelo passante per il punto P.

Per determinare il piano che contiene le due rette è sufficiente prendere due punti di una retta ed un terzo dell’altra e trovare il piano passante per questi tre punti.

$A(0,0,0)$ con $t=0$ e $B(1,2,1)$ con $t=1$ appartengono alla prima retta mentre $C(0,0,3)$ appartiene alla seconda retta.

Adesso sostituendo questi punti all’equazione generica del piano cartesiano

$ax+by+cz+d=0$

devo

$\left\{\begin{matrix} d=0\\ a+2b+c=0\\ 3c+d=0 \end{matrix}\right.$

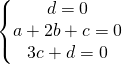
che risolto dà:

$\left\{\begin{matrix} d=0\\ c=0\\ a=-2b \end{matrix}\right.$

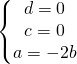
L’equazione del piano diventa:

$-2bx+by=0$

divido per b

$-2x+y=0$

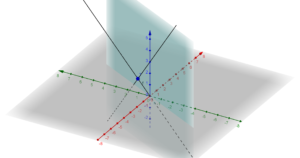
Adesso trovo il piano passante per il punto P

$a-2c+d=0$

e pongo la condizione che deve esser parallelo a quello appena trovato ossia

$-\cfrac{2}{a}=\cfrac{1}{b}=\cfrac{0}{c}$

$-2b=a$

$c=0$

$d=2b$

e l’equazione del piano passante per P e parallelo alle due rette ha equazione:

$-2x+y+2=0$

[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Geometria nello spazio: esercizio 2[:]

Pubblicato il 12 Maggio 2017 da admin

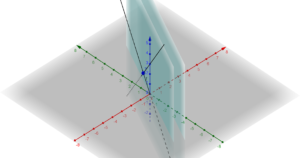
[:it]

Guido Borelli

Una sfera, il cui centro è il punto $k(-2,-1,2)$ è tangente al piano $\Alpha$ di equazione $2x-2y+z-9=0$ . Qual è il punto di tangenza? Qual è il raggio della sfera?

Sviluppo

Il primo passo è determinare il raggio della sfera attraverso la determinazione della distanza tra il centro ed il piano:

$r=\cfrac{\left | ak_{x}+bk_{y}+ck_{z}+d \right |}{\sqrt{a^{2}+b^{2}+c^{2}}}$

dove con $k_{x},k_{y},k_{z}$ sono le tre coordinate del centro, e a,b,c,d sono i rispettivi coefficienti numerici di $x,y,z$ ed il termine noto.

La relazione precedente diventa quindi:

$\cfrac{\left | 2\cdot \left (-2 \right )+ \left (-2 \right )\cdot\left ( -1 \right )+1\cdot 2-9 \right |}{\sqrt{2^{2}+\left ( -2 \right )^{2}+1^{2}}}=\cfrac{\left | -4+2+2-9 \right |}{\sqrt{4+4+1}}=3$

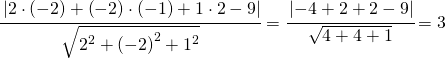
L’equazione della sfera generica è:

$\left ( x-k_{x} \right )^{2}+\left ( y-k_{y} \right )^{2}+\left ( z-z_{x} \right )^{2}=r^{2}$

Sostituendo i valori numerici diventa:

$\left ( x+2 \right )^{2}+\left ( y+1 \right )^{2}+\left ( z-2 \right )^{2}=3^{2}$

metto a sistema l’equazione della sfera con quella del piano ed ho il punto di tangenza:

$\left\{\begin{matrix} \left ( x+2 \right )^{2}+\left ( y+1 \right )^{2}+\left ( z-2 \right )^{2}=3^{2}\\ 2x-2y+z-9=0 \end{matrix}\right.$

se continuassi tale metodo mi troverei però un’equazione in due incognite infatti avrò:

$5x^2+5y^2-22x+28y-8xy-4=0$

Il metodo risolutivo è allora il seguente.

I coefficienti numerici del piano rappresentano le coordinate del vettore perpendicolare al piano, ed il centro rappresenta proprio un punto che appartiene alla retta cercata che avrà equazione parametrica:

$\left\{\begin{matrix} x=-2+2t\\ y=-1-2t\\ z=2+t \end{matrix}\right.$

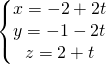
adesso si sostituiscono i valori nell’equazione del piano determinando t:

$\left ( -2+2t \right )2-2\left ( -1-2t \right )+2+t-9=0$

$-4+4t+2+4t+2+t-9=0$

$t=1$

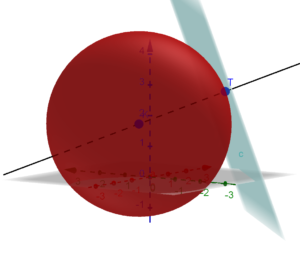
Adesso si sostituisce il valore trovato nell’equazione parametrica del piano e si trova il punto d’intersezione.

x=0

y=-3

z=3

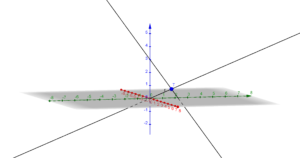
Graficamente si ha la seguente situazione:

[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Test sui monomi[:]

Pubblicato il 12 Maggio 2017 da admin

[:it]

Guido Borelli

[WpProQuiz 49][:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Verifica conclusiva su Power Point e concetti di base sulla teoria dell’informazione[:]

Pubblicato il 10 Maggio 2017 da admin

[:it]

Guido Borelli

13 temi da sviluppare

Tipi di rete LAN, WAN, MAN
Trasmissione a pacchetti
email (SMTP, POP3)
Social Forum
Tutela della salute: illuminazione, corretta postazione di lavoro, ambiente
Sicurezza
Virus
CopyRight
Hardware
software
Firma Digitale
Documenti digitali
Velocità di trasmissione e scaricamento file.

Il power Point dovrà contenere:

Dieci slide
almeno 4 immagini
una diapositiva titolo
una diapositiva Titolo e contenuto
almeno un grafico (a piacere)
almeno 5 forme
almeno una nota per il relatore
il numero di pagina ad esclusione della slide di tipo titolo
la data solo nell’ultima diapositiva
il nome su tutte le diapositive
un indice con il link alle diapositive che lo sviluppano
che ogni slide possa avere una transizione
che ogni slide abbia un’animazione a scelta

[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Approfondimenti Retta sul piano cartesiano in forma parametrica e vettore direzione[:]

Pubblicato il 7 Maggio 2017 da admin

[:it]

Guido Borelli

Normalmente una retta viene sempre definita nella forma

$y= mx +q$

o nella forma

$ax+by+c=0$

che viene utilizzata solo quando si deve determinare la distanza tra un punto ed una retta.

Che significato hanno $a$ e $b$ ?

Essi rappresentano proprio le componenti del vettore $v_{\perp }\left ( a;b \right )$ perpendicolare alla retta.

Graficamente si vede benissimo tale fatto.

La retta $3x+2y+5=0$

ha vettore $v_{\perp }\left ( 3;2 \right )$

Date due rette

$ax+by+c=0$

$a'x+b'y+c=0$

Condizione di parallelismo

Saranno parallele quando i due vettori saranno una combinazione lineare dell’uno rispetto all’altro quindi:

$a=\alpha a'$

$b=\alpha b'$

o meglio:

$\cfrac{a}{a'}=\cfrac{b}{b'}$

graficamente si vede la cosa:

date le rette

$2x+2y+5=0$

$9x+6y+2=0$

sono parallele

e si vede che i due vettori sono sovrapposti ed uno è proprio multiplo dell’altro.

Condizione di perpendicolarità

In seguito alla definizione di prodotto scalare tra due vettori, saranno perpendicolari due rette se

$a\cdot a'+b\cdot b'=0$

Graficamente.

Se si hanno le due rette

$2x+2y+5=0$ con $m_{\perp }(2,2)$

$9x+6y+2=0$ con $v_{\perp }(9,6)$

Retta in forma parametrica

Tale rappresentazione utilizza il vettore direzione. Vi sono infinite rappresentazione della retta in forma parametrica perché sono infiniti i vettori che sono paralleli ad una retta.

Tale vettore si chiama vettore direzione.

Ad esempio:

$\left\{\begin{matrix} x=3+2t\\ y=2+5t \end{matrix}\right.$

il vettore direzione ha le coordinate che sono i coefficienti di t

$v(2,5)$

E’ molto più agevole avere la retta in forma parametrica per farne il grafico.

E’ la rappresentazione parametrica della retta

$5x-2y-11=0$

Passaggio dalla forma parametrica alla forma implicita.

Si risolve il sistema in funzione di t e si confrontano i due valori di t trovati.

Ad esempio:

$\left\{\begin{matrix} x=3+2t\\ y=2+5t \end{matrix}\right.$

$\left\{\begin{matrix} t=\cfrac{x-3}{2}\\ t=\cfrac{y-2}{5} \end{matrix}\right.$

$\cfrac{x-3}{2}=\cfrac{y-2}{5}$

$5x-15=2y-4$

$5x-2y-11=0$

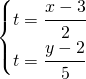
Passaggio dalla forma implicita alla forma parametrica

Vi sono vari metodi.

Uno è il seguente.

La forma implicita

$ax+by+d=0$

fornisce il vettore $v_{\perp }(a,b)$ , il vettore direzione è perpendicolare a questo per cui avrà coordinate $v(b,-a)$

La forma parametrica generale è:

$\left\{\begin{matrix} x=x_{0}+lt\\ y=y_{0}+mt \end{matrix}\right.$

dove v(l,m) è il vettore direzione e $P(x_{0},y_{0})$ sono le coordinate di un punto appartenente alla retta.

Ad esempio se ho la retta:

$x+2y+5=0$

il vettore $v_{\perp }(1,2)$ , il vettore direzione è $v(2,-1)$ ,

$\left\{\begin{matrix} x=x_{0}+2t\\ y=y_{0}-t \end{matrix}\right.$

Adesso prendo il punto $P(0,-\cfrac{5}{2})$ che appartiene alla retta.

$\left\{\begin{matrix} x=0+2t\\ y=-\cfrac{5}{2} -t \end{matrix}\right.$ [:]

Pubblicato in Senza categoria | Contrassegnato retta, retta parametrica, rette prallele | Lascia un commento

[:it]Distanza punto piano[:]

Pubblicato il 7 Maggio 2017 da admin

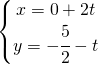[:it]

Cole Rise

La distanza di un punto da un piano non è che la trasposizione nello spazio della distanza di un punto da una retta sul piano cartesiano.

La distanza punto retta sul piano cartesiano

Data la retta nella forma

$ax+by+c=0$

ed il punto $P\left ( x_{p};y_{p} \right )$

la distanza sarà:

$d=\cfrac{\left | ax_{p}+by_{p}+c \right |}{\sqrt{a^{2}+b^{2}}}$

la distanza di un punto nello spazio e di un piano sarà

Dato un piano nella forma

ax+by+cz+d=0

ed il punto $P\left ( x_{p};y_{p};z_{p} \right )$

la distanza sarà:

$d=\cfrac{\left | ax_{p}+by_{p}+cz_{p}+d \right |}{\sqrt{a^{2}+b^{2}+c^{2}}}$

[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Testo maturità scientifico anno 2015[:]

Pubblicato il 7 Maggio 2017 da admin

[:it]

Guido Borelli

Questi sono i problemi e i quesiti della maturità anno 2015:

matematica-scientifico-problema1

matematica-scientifico-problema2

matematica-scientifico-questionario

[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Posizione reciproca tra piani[:]

Pubblicato il 7 Maggio 2017 da admin

[:it]Dati due piani:

$ax+by+cz+d=0$

$a'x+b'y+c'z+d'=0$

PIANI PARALLELI

Quando le componenti del vettore $v_{\perp }$ e $v'_{\perp }$ sono uno combinazione lineare dell’altro.

Ossia:

$a=\alpha a'$

$b=\alpha b'$

$c=\alpha c'$

in maniera più compatta e semplice:

$\cfrac{a}{a'}=\cfrac{b}{b'}=\cfrac{c}{c'}$

Ad esempio i piani:

$2x-6y+4z+1=0$

$4x-13y+8z+1=0$

sono paralleli come si vede nel grafico:

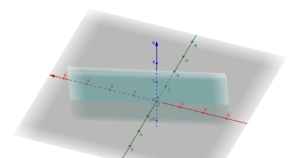
PIANI PERPENDICOLARI

Quando il prodotto scalare dei vettori $v_{\perp }$ e $v'_{\perp }$ è nullo.

Il prodotto scalare è:

$\vec{a}\cdot \vec{b}=\left | \vec{a} \right |\cdot \left | \vec{b} \right |\cdot \cos \vartheta$

quando sono perpendicolari $\cos \vartheta=0$

e quindi la condizione è

$a\cdot a'+b\cdot b'+c\cdot c'=0$

Ad esempio i piani

$2x-4y+2z+5=0$

$3x+2y+z+1=0$

sono perpendicolari infatti

$2\cdot 3 -4 \cdot 2 + 2 \cdot 1 =0$

e graficamente

[:]

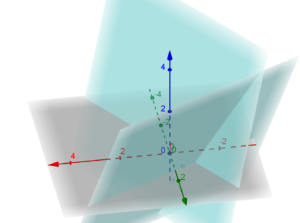
Pubblicato in Senza categoria | Lascia un commento

Verifica finale di Excel

[:it]Geometria nello spazio: esercizio 1[:]

[:it]Geometria nello spazio: esercizio 3[:]

[:it]Geometria nello spazio: esercizio 2[:]

[:it]Test sui monomi[:]

[:it]Verifica conclusiva su Power Point e concetti di base sulla teoria dell’informazione[:]

[:it]Approfondimenti Retta sul piano cartesiano in forma parametrica e vettore direzione[:]

[:it]Distanza punto piano[:]

[:it]Testo maturità scientifico anno 2015[:]

[:it]Posizione reciproca tra piani[:]

Registrazione

Categorie

Articoli recenti

Commenti recenti

Meta

Categorie

Articoli recenti

Commenti recenti

Meta

Whymatematica