[:it]Geometria nello spazio: esercizio 1[:]

[:it]

Guido Borelli

Data la sfera di centro $C(2,-3,0)$ e raggio 2 determinare le equazioni dei due piani tangenti e paralleli al piano $3x-y+z=0$

Svolgimento

Essendo piano paralleli al piano dato soddisferanno alla relazione

$\cfrac{3}{a}=-\cfrac{1}{b}=\cfrac{1}{c}$

$a=-3b$

$c=-b$

L’equazione del piano diventa:

$-3bx+by-bz+d=0$

Adesso pongo la distanza tra il centro della sfera e i piani uguale alla lunghezza del raggio

$r=\cfrac{\left |ac_^{x}+bc_{y}+cc_{z}+d \right |}{\sqrt{a^{2}+b^{2}+c^{2}}}$

sostituendo adesso i valori numerici si ha:

$r=\cfrac{\left |-3b\cdot 2-3b+d \right |}{\sqrt{9b^{2}+b^{2}+b^{2}}}=2$

$r=\cfrac{\left |-9b+d \right |}{\sqrt{11b^{2}}}=2$

Essendovi il modulo avrò le seguenti due equazioni

$-9b+d=2b\sqrt{11}$ che ha come soluzione

$d=b(2\sqrt{11}+9)$

$9b-d=2b\sqrt{11}$

$d=b(-2\sqrt{11}+9)$

Le equazioni dei piani sono quindi:

$-3x+y-z+2\sqrt{11}+9=0$

$-3x+y-z-2\sqrt{11}+9=0$

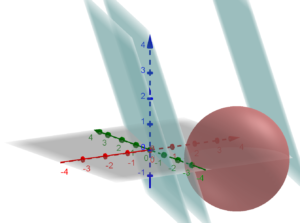
Graficamente si ha:

[:]

Questa voce è stata pubblicata in Senza categoria. Contrassegna il permalink.