[:it]

Catrin-Welz-Stein
Per risolvere una disequazione si richiede soltanto di saper risolvere un’equazione di primo grado, valgono le stesse regole:
- il coefficiente che moltiplica la x deve sempre essere positivo
- per arrivare al punto precedente si può:
- moltiplicare a sinistra e a destra per la stessa quantità,
- sommare a sinistra e a destra per la stessa quantità
- dividere a sinistra e a destra per la stessa quantità
Ricordarsi che:
il segno “>” significa maggiore,
il segno “<” significa minore.
Esercizi di base che riprendono le equazioni di primo grado:
Esercizi di tipo A
Ne sviluppo uno come esempio
![]()
![]()
![]()
Cosa significa il risultato?
Che tutti i numeri maggiori di 13 fanno sì che la disequazione ![]() sia effettivamente maggiore di zero.
sia effettivamente maggiore di zero.
| A.1. |
|
| A.2. |
|
| A.3. |
|
| A.4. |
|
| A.5. |
|
| A.6. |
|
| A.7. |
|
| A.8. |
|
| A.9. |
|
| A.10. |
Esercizi di base di tipo B
Ne sviluppo uno come esempio:
![]()
divido entrambi i membri per il numero che moltiplica la ![]()
![]()
si semplifica il 2 del numeratore con il 2 del denominatore del membro a sinistra dell’uguale.
![]()
![]()
| B.1. |
|
| B.2. |
|
| B.3. |
|
| B.4. |
|
| B.5. |
|
| B.6. |
|
| B.7. |
|
| B.8. |
|
| B.9. |
|
| B.10. |
Esercizi di base di tipo C
Sviluppo un esempio:
![]()
moltiplico entrambi i membri per 6
![]()
quindi semplifico il 6 del numeratore con il 6 del denominatore del membro a sinistra dell’uguale.
![]()
il risultato è
![]()
| C.1. |
|
| C.2. |
|
| C.3. |
|
| C.4. |
|
| C.5. |
|
| C.6. |
|
| C.7. |
|
| C.8. |
|
| C.9. |
|
| C.10. |
Esercizi base di tipo D: cambio del verso della disequazione
Ne sviluppo uno come esempio
![]()
![]()
![]()
siccome non ha significato indicare come soluzione -x moltiplico a sinistra e a destra per -1 ma DEVO CAMBIARE IL VERSO DELLA DISEQUAZIONE
![]()
![]()
| D.1. |
|
| D.2. |
|
| D.3. |
|
| D.4. |
|
| D.5. |
|
| D.6. |
|
| D.7. |
|
| D.8. |
|
| D.9. |
|
| D.10. |
Livello sufficiente [6].
| 6.1. |
|
| 6.2. |
|
| 6.3. |
![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{1}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-34bc2ff7aead278c493a9716fe841b55_l3.png) |
| 6.4. |
![Rendered by QuickLaTeX.com \left [ x> \cfrac{5}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-90c121580c491dbfbf8f050df9602243_l3.png) |
| 6.5. |
![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{10}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-410949a150ffd3eb758a161cc340088d_l3.png) |
| 6.6. |
Ogni valore di x |
| 6.7. |
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{1}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-880015ba231003b8163ca46a376d0f66_l3.png) |
| 6.8. |
nessun valore di x |
| 6.9 |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{8}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-88d4b62eabf58f96bdc307163bc733d8_l3.png) |
| 6.10. |
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{5}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d3a0c1c33cde37730ec2bd521f999d0c_l3.png) |
| 6.11. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{7}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-cc0b925830708c1a3f142d9e97681614_l3.png) |
| 6.12. |
|
| 6.13. |
|
| 6.14. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{2}{9} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7d0d36a6cfb1dbb3430a7f7d20c8829c_l3.png) |
| 6.15. |
|
| 6.16. |
sempre vera |
| 6.17. |
nessun valore di a |
| 6.18. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{2}{9} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7d0d36a6cfb1dbb3430a7f7d20c8829c_l3.png) |
| 6.19. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{4}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9f9c09fec77f628e93139e0abf1734aa_l3.png) |
| 6.20. |
|
| 6.21. |
ogni valore di x |
| 6.22. |
nessun valore di x |
| 6.23. |
Livello discreto: richiede manualità con le frazioni e lo sviluppo delle parentesi [7]
| 7.1. |
![Rendered by QuickLaTeX.com \left [x<\cfrac{1}{6}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2a63066896d443b89558d1f9aefb3d83_l3.png) |
| 7.2. |
|
| 7.3. |
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2de43c2738ee6f1ab07ce36e9153b791_l3.png) |
| 7.4. |
|
| 7.5. |
|
| 7.6. |
|
7.7. ![Rendered by QuickLaTeX.com \cfrac{1}{5}\left ( x-2 \right )-\left [ 1+2x-\left ( x+\cfrac{1}{2} \right ) \right ]\leq 1](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-36f4af288d2c0cf8680b77c48afe0de9_l3.png) |
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{19}{8} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5b393050de4f374b692e0a9f794b77f9_l3.png) |
| 7.8. |
nessuna soluzione |
| 7.9. |
Verso un livello buono e con una certa sicurezza [8]
| 8.1. |
![Rendered by QuickLaTeX.com \left [ x<-\cfrac{2}{7} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ccf45ccc6650a4b66a098051b4794f60_l3.png) |
8.2. 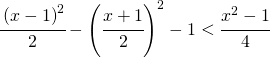 |
|
8.3. ![Rendered by QuickLaTeX.com 9x+20\geq 2\left [ \cfrac{29}{4}-6\left ( x-1 \right )+9x-\cfrac{9}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-60c738380ef84b193542335c382f0b8b_l3.png) |
![Rendered by QuickLaTeX.com \left [ x\geq \cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-6c1e262716e69477c58bbb99e19158af_l3.png) |
| 8.4. |
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{4}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-233dc8229b397df8faadec86bc3d1bf5_l3.png) |
Per un livello ottimo [9]
| 9.1. |
|
| 9.2. |
![Rendered by QuickLaTeX.com \left [ x<\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5fe59560429192c0c5955eed241d455b_l3.png) |
soluzioni[:en]

Catrin-Welz-Stein
Per risolvere una disequazione si richiede soltanto di saper risolvere un’equazione di primo grado, valgono le stesse regole:
- il coefficiente che moltiplica la x deve sempre essere positivo
- per arrivare al punto precedente si può:
- moltiplicare a sinistra e a destra per la stessa quantità,
- sommare a sinistra e a destra per la stessa quantità
- dividere a sinistra e a destra per la stessa quantità
Livello sufficiente: richiedono di ricordarsi le regole per la soluzione delle equazioni di primo grado.
| 6.1. |
|
| 6.2. |
|
| 6.3. |
![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{1}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-34bc2ff7aead278c493a9716fe841b55_l3.png) |
| 6.4. |
![Rendered by QuickLaTeX.com \left [ x> \cfrac{5}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-90c121580c491dbfbf8f050df9602243_l3.png) |
| 6.5. |
![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{10}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-410949a150ffd3eb758a161cc340088d_l3.png) |
| 6.6. |
Ogni valore di x |
| 6.7. |
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{1}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-880015ba231003b8163ca46a376d0f66_l3.png) |
| 6.8. |
nessun valore di x |
| 6.9 |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{8}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-88d4b62eabf58f96bdc307163bc733d8_l3.png) |
| 6.10. |
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{5}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d3a0c1c33cde37730ec2bd521f999d0c_l3.png) |
| 6.11. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{7}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-cc0b925830708c1a3f142d9e97681614_l3.png) |
| 6.12. |
|
| 6.13. |
|
| 6.14. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{2}{9} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7d0d36a6cfb1dbb3430a7f7d20c8829c_l3.png) |
| 6.15. |
|
| 6.16. |
sempre vera |
| 6.17. |
nessun valore di a |
| 6.18. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{2}{9} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7d0d36a6cfb1dbb3430a7f7d20c8829c_l3.png) |
| 6.19. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{4}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9f9c09fec77f628e93139e0abf1734aa_l3.png) |
| 6.20. |
|
| 6.21. |
ogni valore di x |
| 6.22. |
nessun valore di x |
| 6.23. |
Livello discreto: richiede manualità con le frazioni e lo sviluppo delle parentesi
| 7.1. |
![Rendered by QuickLaTeX.com \left [x<\cfrac{1}{6}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2a63066896d443b89558d1f9aefb3d83_l3.png) |
| 7.2. |
|
| 7.3. |
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2de43c2738ee6f1ab07ce36e9153b791_l3.png) |
| 7.4. |
|
| 7.5. |
|
| 7.6. |
|
7.7. ![Rendered by QuickLaTeX.com \cfrac{1}{5}\left ( x-2 \right )-\left [ 1+2x-\left ( x+\cfrac{1}{2} \right ) \right ]\leq 1](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-36f4af288d2c0cf8680b77c48afe0de9_l3.png) |
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{19}{8} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5b393050de4f374b692e0a9f794b77f9_l3.png) |
| 7.8. |
nessuna soluzione |
| 7.9. |
Verso un livello buono e con una certa sicurezza
| 8.1. |
![Rendered by QuickLaTeX.com \left [ x<-\cfrac{2}{7} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ccf45ccc6650a4b66a098051b4794f60_l3.png) |
8.2. 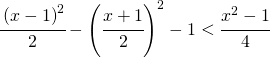 |
|
8.3. ![Rendered by QuickLaTeX.com 9x+20\geq 2\left [ \cfrac{29}{4}-6\left ( x-1 \right )+9x-\cfrac{9}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-60c738380ef84b193542335c382f0b8b_l3.png) |
![Rendered by QuickLaTeX.com \left [ x\geq \cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-6c1e262716e69477c58bbb99e19158af_l3.png) |
| 8.4. |
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{4}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-233dc8229b397df8faadec86bc3d1bf5_l3.png) |
Per un livello ottimo
| 9.1. |
|
| 9.2. |
![Rendered by QuickLaTeX.com \left [ x<\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5fe59560429192c0c5955eed241d455b_l3.png) |
soluzioni[:de]

Catrin-Welz-Stein
Per risolvere una disequazione si richiede soltanto di saper risolvere un’equazione di primo grado, valgono le stesse regole:
- il coefficiente che moltiplica la x deve sempre essere positivo
- per arrivare al punto precedente si può:
- moltiplicare a sinistra e a destra per la stessa quantità,
- sommare a sinistra e a destra per la stessa quantità
- dividere a sinistra e a destra per la stessa quantità
Livello sufficiente: richiedono di ricordarsi le regole per la soluzione delle equazioni di primo grado.
| 6.1. |
|
| 6.2. |
|
| 6.3. |
![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{1}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-34bc2ff7aead278c493a9716fe841b55_l3.png) |
| 6.4. |
![Rendered by QuickLaTeX.com \left [ x> \cfrac{5}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-90c121580c491dbfbf8f050df9602243_l3.png) |
| 6.5. |
![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{10}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-410949a150ffd3eb758a161cc340088d_l3.png) |
| 6.6. |
Ogni valore di x |
| 6.7. |
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{1}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-880015ba231003b8163ca46a376d0f66_l3.png) |
| 6.8. |
nessun valore di x |
| 6.9 |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{8}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-88d4b62eabf58f96bdc307163bc733d8_l3.png) |
| 6.10. |
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{5}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d3a0c1c33cde37730ec2bd521f999d0c_l3.png) |
| 6.11. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{7}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-cc0b925830708c1a3f142d9e97681614_l3.png) |
| 6.12. |
|
| 6.13. |
|
| 6.14. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{2}{9} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7d0d36a6cfb1dbb3430a7f7d20c8829c_l3.png) |
| 6.15. |
|
| 6.16. |
sempre vera |
| 6.17. |
nessun valore di a |
| 6.18. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{2}{9} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7d0d36a6cfb1dbb3430a7f7d20c8829c_l3.png) |
| 6.19. |
![Rendered by QuickLaTeX.com \left [ x>\cfrac{4}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9f9c09fec77f628e93139e0abf1734aa_l3.png) |
| 6.20. |
|
| 6.21. |
ogni valore di x |
| 6.22. |
nessun valore di x |
| 6.23. |
Livello discreto: richiede manualità con le frazioni e lo sviluppo delle parentesi
| 7.1. |
![Rendered by QuickLaTeX.com \left [x<\cfrac{1}{6}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2a63066896d443b89558d1f9aefb3d83_l3.png) |
| 7.2. |
|
| 7.3. |
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2de43c2738ee6f1ab07ce36e9153b791_l3.png) |
| 7.4. |
|
| 7.5. |
|
| 7.6. |
|
7.7. ![Rendered by QuickLaTeX.com \cfrac{1}{5}\left ( x-2 \right )-\left [ 1+2x-\left ( x+\cfrac{1}{2} \right ) \right ]\leq 1](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-36f4af288d2c0cf8680b77c48afe0de9_l3.png) |
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{19}{8} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5b393050de4f374b692e0a9f794b77f9_l3.png) |
| 7.8. |
nessuna soluzione |
| 7.9. |
Verso un livello buono e con una certa sicurezza
| 8.1. |
![Rendered by QuickLaTeX.com \left [ x<-\cfrac{2}{7} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ccf45ccc6650a4b66a098051b4794f60_l3.png) |
8.2. 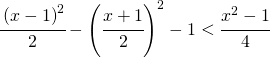 |
|
8.3. ![Rendered by QuickLaTeX.com 9x+20\geq 2\left [ \cfrac{29}{4}-6\left ( x-1 \right )+9x-\cfrac{9}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-60c738380ef84b193542335c382f0b8b_l3.png) |
![Rendered by QuickLaTeX.com \left [ x\geq \cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-6c1e262716e69477c58bbb99e19158af_l3.png) |
| 8.4. |
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{4}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-233dc8229b397df8faadec86bc3d1bf5_l3.png) |
Per un livello ottimo
| 9.1. |
|
| 9.2. |
![Rendered by QuickLaTeX.com \left [ x<\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5fe59560429192c0c5955eed241d455b_l3.png) |
soluzioni[:]
