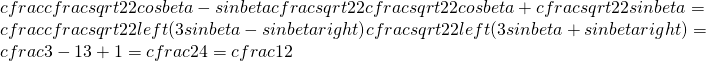Limiti infiniti – asintoto verticale

Pubblicato il 1 Maggio 2012 da admin

Jacek Yerka

Il concetto di infinito lo si affronta solo all’ultimo anno delle superiori come se esso non fosse già ben presente nella quotidianità.

(1) \underset{x\rightarrow c}{lim}f(x)=+\infty.

(2) \underset{x\rightarrow c}{lim}f(x)=-\infty.

Per dare un’applicazione pratica immediata si sappia che tale limite permette di definire l’asintoto verticale.

Un asintoto è una retta a cui la funzione di partenza tende ad avvicinarsi senza però mai toccarla: asintoto=senza sintesi ossia privo di unione, nel senso che le curve non si toccano.

Si noi che nella (1) e nella (2) ho fatto uso di +\infty e -\infty ossia esiste un infinito positivo ed un infinito negativo: si pensi ai numeri positivi: essi sono infiniti, in senso positivo; mentre quelli negativi sono infiniti in senso negativo.

Per determinare gli asintoti verticali si considerino i punti in cui la funzione non è definita ossia quei punti che sono esclusi dal dominio.

Esempio pratico immediato:

Si consideri la funzione:

f(x)=\cfrac{1}{x^{2}}

essa è definita per ogni valore di x escluso il punto 0.

Studiamo cosa accade un tale punto:

\underset{x\rightarrow0}{lim}\cfrac{1}{x^{2}}=+\infty

ossia se si sostituiscono valori sempre più piccoli di x si noti che il valore della funzione assume sempre valori più grandi: al limite, appunto, ci si trova  con un numero così grande che sinteticamente viene scritto +\infty .

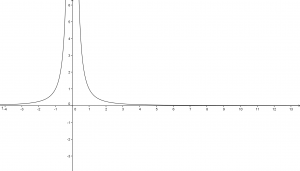
Per completezza e per dare una rappresentazione grafica tale curva, sul piano cartesiano ha il seguente andamento:

Tale curva ha proprio un asintoto verticale coincidente con l’asse delle ordinate.

 

 

Pubblicato in Senza categoria | Lascia un commento

Limiti: esercizi sulla prima definizione

Pubblicato il 1 Maggio 2012 da admin

Jacek Yerka

 

1) \underset{x\rightarrow9}{lim}3-\sqrt{x}.

2) \underset{x\rightarrow2}{lim}\cfrac{x+2}{3x}.

3) \underset{x\rightarrow2}{lim}3^{2-x}.

4) \underset{x\rightarrow1}{lim}\cfrac{x^{2}-3x+2}{x+4}.

5) \underset{x\rightarrow3}{lim}\left(\cfrac{4}{x}+\cfrac{3x}{x+3}\right).

6) \underset{x\rightarrow-1}{lim}\left(\sqrt{1+x^{2}}\right).

7) \underset{x\rightarrow0}{lim}\cfrac{x^{2}-2}{\sqrt{x+4}}.

8) \underset{x\rightarrow1}{lim}\cfrac{e^{x}-2x}{e^{x}-2}.

Pubblicato in Senza categoria | Lascia un commento

Il m.cm. e M.C.D. tra monomi

Pubblicato il 24 Aprile 2012 da admin

Prima di affrontarle il mcm e MCD per i monomi è interessante richiamarli dal punto di vista algebrico:

m.c.m: il minimo comune multiplo è il prodotto di tutti i fattori comuni e non comuni presi con il massimo esponente.

M.C.D. il massimo comune divisore invece è il prodotto dei SOLI fattori comuni presi con l’esponente più basso.

Ecco una lezione interessante sul mcm tra monomi:

Ecco una lezione interessante sul M.C.D. tra i monomi

Pubblicato in Uncategorized | Lascia un commento

L’infinito

Pubblicato il 23 Aprile 2012 da admin

In matematica il concetto di infinito procura spesso grandi dubbi esattamente come la più grande poesia di ogni tempo che il genio di Leopardi ci ha regalato:

« Sempre caro mi fu quest’ermo colle,
e questa siepe, che da tanta parte
dell’ultimo orizzonte il guardo esclude.
Ma sedendo e mirando, interminati
spazi di là da quella, e sovrumani
silenzi, e profondissima quïete
io nel pensier mi fingo, ove per poco
il cor non si spaura. E come il vento
odo stormir tra queste piante, io quello
infinito silenzio a questa voce
vo comparando: e mi sovvien l’eterno,
e le morte stagioni, e la presente
e viva, e il suon di lei. Così tra questa
immensità s’annega il pensier mio:
e il naufragar m’è dolce in questo mare. »

Tornando però nell’ambito matematico l’infinito è un concetto collegato a quello di asintoto. L’asintoto è una retta immaginaria a cui la funzione cerca di avvicinarsi ma a cui non arriva mai.

E’ come il concetto di velocità della luce: ad essa non ci si può mai arrivare ma solo tendere in quanto per arrivarci bisognerebbe avere una massa infinitamente piccola se non nulla; tale velocità infatti è raggiungibile solo dall’energia!

 

Pubblicato in Uncategorized | Lascia un commento

I limiti: introduzione

Pubblicato il 23 Aprile 2012 da admin

Enrico Prampolini

Il concetto di limite è fondamentale per capire verso quale valore tende una funzione. In particolare mi interessa dettare delle regole pratiche per poterne fare un protocollo di attuazione immediata:

Ecco la sua forma più semplice ed immediata:

\underset{x\rightarrow x_{0}}{lim}f(x)=f(x_{0})

Come si legge?

Il limite per x che tende a x_{0} di f(x) vale f(x_{0}).

Ho sostituito il valore a cui tende la x nella funzione di partenza.

es.1

\underset{x\rightarrow 2}{lim}(3x+1)=3 \cdot 2+1=7

In questo caso il valore a cui tende la funzione coincide con il valore stesso della funzione in quel punto. Sembra una tautologia ma in realtà non è così: sia che ci si avvicini da destra che da sinistra a quel punto, il risultato non cambia.

Il concetto di limite destro e sinistro è fondamentale nello studio di funzione:  a seconda che ci si avvicini da sinistra o da destra il valore della funzione potrebbe assumere dei valori diversi.

REGOLA PRATICA

Per sviluppare un limite la prima operazione è proprio quella di sostituire il valore a cui tende la x alla funzione.

Pubblicato in Senza categoria | Lascia un commento

Trigonometria: per esercitarsi sulle formule di addizione: problema 3

Pubblicato il 20 Aprile 2012 da admin

Fortunato Depero

3) Dato alpha;beta che appartengono al primo quadrante e che:

tanalpha=cfrac{1}{2}

cothbeta=3

Dimostrare che:

alpha+beta=cfrac{pi}{4}

Sviluppo

(1) alpha=cfrac{pi}{4}-beta

cothbeta=cfrac{cosbeta}{sinbeta}=3 ossia

(2) cosbeta=3cdotsinbeta

Adesso utilizzo la (1)

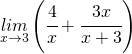tanalpha=cfrac{sinalpha}{cosalpha}=cfrac{sinleft(cfrac[l]{pi}{4}-betaright)}{cosleft(cfrac{pi}{4}-betaright)}=cfrac{sincfrac{pi}{4}cosbeta-sinbetacoscfrac{pi}{4}}{coscfrac{pi}{4}cosbeta+sincfrac{pi}{4}sinbeta}=cfrac{1}{2}

quindi utilizzando anche la (2) e sviluppando il seno di 45° ed il coseno di 45° ho:

cfrac{cfrac{sqrt{2}}{2}cosbeta-sinbetacfrac{sqrt{2}}{2}}{cfrac{sqrt{2}}{2}cosbeta+cfrac{sqrt{2}}{2}sinbeta}=cfrac{cfrac{sqrt{2}}{2}left(3sinbeta-sinbetaright)}{cfrac{sqrt{2}}{2}left(3sinbeta+sinbetaright)}=cfrac{3-1}{3+1}=cfrac{2}{4}=cfrac{1}{2}

Pubblicato in Uncategorized | Lascia un commento

Trigonometria: per esercitarsi sulle formule di addizione (problema 2)

Pubblicato il 20 Aprile 2012 da admin

Gino Severini

2) Dato un triangolo i cui angoli alpha;beta;gamma seguono le seguenti relazioni:

cosalpha=cfrac{12}{13}

cosbeta=cfrac{4}{5}

dire se tale triangolo è acutangolo o ottusangolo e determinare tangamma.

Sviluppo

Un triangolo si dice acutangolo quando ha tutti e tre gli angoli minori di 90°.

Un triangolo si dice ottusangolo quando un angolo è ottuso ossia maggiore di 90°.

Nel caso specifico cosalpha è positivo per cui 0<alpha<cfrac{pi}{2} non potrà mai essere tra cfrac{3}{2}pi<alpha<2pi perchè la somma degli angoli interni di un triangolo è sempre 180°.

Lo stesso ragionamento vale per cosbeta.

Quindi 0<alpha;beta<cfrac{pi}{2} e non si può ancora dire se il terzo angolo sia maggiore o minore di 90° condizione che ci fa affermare se avere un acutangolo o un ottusangolo.

Allora, sempre per la relazione fondamentale che la somma degli angoli interni di un triangolo è 180°, gamma=pi-(alpha+beta).

(1) tanleft[pi-(alpha+beta)right]=-tanleft(alpha+betaright)=cfrac{sinalphacosbeta+sinbetacosalpha}{sinalphasinbeta-cosalphacosbeta}

Adesso ho:

(2) sinalpha=pmsqrt{1-left(cfrac{12}{13}right)^{2}}=pmsqrt{1-cfrac{144}{169}}=pmcfrac{5}{13}

prendo il valore positivo in quanto 0<alpha<cfrac{pi}{2}.

(3) sinbeta=pmsqrt{1-left(cfrac{4}{5}right)^{2}}=pmsqrt{1-cfrac{16}{25}}=pmcfrac{3}{5}

prendo il valore positivo in quanto 0<beta<cfrac{pi}{2}.

Adesso sostituisco i valori dati dal problema e la (2) e la (3) nella (1) e risulta:

tangamma=cfrac{cfrac{5}{13}cdotcfrac{4}{5}+cfrac{3}{5}cdotcfrac{12}{13}}{cfrac{5}{13}cdotcfrac{3}{5}-cfrac{12}{13}cdotcfrac{4}{5}}=-cfrac{56}{33}

La tangente assume un valore negativo tra cfrac{pi}{2}<gamma<cfrac{3}{2}pi

per cui alla fine mi troverò un ottusangolo!

 

 

Pubblicato in Uncategorized | Lascia un commento

Trigonometria: per esercitarsi sulle formule di addizione (problema 1)

Pubblicato il 20 Aprile 2012 da admin

Fortunato Depero

1) Dato un triangolo i cui angoli (alpha;beta;gamma) seguono le seguenti relazioni:

cosalpha=-cfrac{1}{sqrt{3}} con 2pi<alpha<cfrac{pi}{2}

cosbeta=cfrac{5}{6} con 0<beta<cfrac{pi}{2}

Determinare il singamma.

Sviluppo:

alpha+beta+gamma=pi ossia

gamma=pi-(alpha+beta)

devo determinare:

(1) singamma=sinleft[pi-(alpha+beta)right]=sin(alpha+beta)=sinalphacosbeta+cosalphasinbeta

in cui ho utilizzato le formule di addizione.

siccome in trigonometria vale la relazione fondamentale che è la diretta conseguenza del teorema di Piragora:

sin^{2}alpha+cos^{2}alpha=1

allora

sinalpha=pmsqrt{1-cos^{2}alpha}=pmsqrt{1-left(-cfrac{1}{sqrt{3}}right)^{2}}=pmsqrt{1-cfrac{1}{3}}=pmsqrt{cfrac{2}{3}}

devo prendere il segno positivo o negativo?

Siccome il sinalpha è positivo per 2pi<alpha<cfrac{pi}{2} allora prendo il segno positivo ed ho quindi:

(2) sinalpha=sqrt{cfrac{2}{3}}

In maniera analoga ho:

sinbeta=pmsqrt{1-left(cfrac{5}{6}right)^{2}}=pmsqrt{1-cfrac{25}{36}}=pmsqrt{cfrac{11}{36}}=pmcfrac{sqrt{11}}{6}

Prendo il segno positivo perchè sinbeta è positivo per 0<beta<cfrac{pi}{2}

quindi:

(3) sinbeta=cfrac{sqrt{11}}{6}

Adesso sostituisco la (2) e la (3) nella (1) prendendo anche i dati di partenza e risulta:

sqrt{cfrac{2}{3}}cdotcfrac{5}{6}-cfrac{sqrt{11}}{6}cdotcfrac{1}{sqrt{3}}=cfrac{5sqrt{2}-sqrt{11}}{6sqrt{3}}

razionalizzando (ossia moltiplicando per sqrt{3} sia il numeratore che il denominatore) il risultato conclusivo diventa:

cfrac{5sqrt{2}-sqrt{11}}{6sqrt{3}}=cfrac{5sqrt{6}-sqrt{33}}{18}

 

Pubblicato in Uncategorized | Lascia un commento

Il triangolo di Tartaglia

Pubblicato il 19 Aprile 2012 da admin

Il triangolo di Tartaglia rimane una pietra miliare che indica il passaggio dai più conosciuti prodotti notevoli a quelli meno usati.

Tale post è stato richiesto da un alunno (A.M.O.) che si chiedeva perchè non si potessero avere i prodotti successivi!

Propedeutico è  esplicitare tutti gli esponenti dei binomi per apprezzare compeltamente la schematizzazione.

\left ( a+b \right )^{2}=a^{2}b^{0}+2a^{1}b^{1}+a^{0}b^{2}

\left ( a+b \right )^{3}=a^{3}b^{0}+3a^{2}b^{1}+3a^{1}b^{2}+a^{0}b^{3}

adesso se  si vuole scrivere l’elevamento a potenza successivo è indispensabile avere il triangolo di Tartaglia:

_______1–> \left ( a+b \right )^{1}

______1- 2- 1 –>\left ( a+b \right )^{2}

_____1-3- 3- 1–>\left ( a+b \right )^{3}

____1 -4- 6- 4- 1–>\left( a+b \right )^{4}

___1 -5 -10- 10- 5- 1–>\left( a+b \right )^{5}

quindi la quarta riga mi fornisce:

\left ( a+b \right )^{4}=a^{4}b^{0}+4a^{3}b^{1}+6a^{2}b^{2}+4a^{1}b^{3}+a^{0}b^{4}

Come si crea il triangolo di Tartaglia?

Ad esempio nella quinta riga il 5 è dato dalla somma dell’1 e del 4 della riga precedente.

Il 10 è dato dalla somma del 4 e del 6 della riga precedente e così via.

Pubblicato in Uncategorized | Lascia un commento

Trigonometria: gli angoli fondamentali – le formule di addizione

Pubblicato il 18 Aprile 2012 da admin

Rene Magritte - Il mistero della natura

Osservando il grafico presente nel post precedente si possono evincere gli angoli fondamentali:

Attenzione però alla seguente notazione:

cfrac{pi}{2}=90^{0}

pi=180^{0}

cfrac{3}{2}pi=270^{0}

2pi=360^{0}

In trigonometria si utilizza sempre tale notazione per indicare il valore degli angoli.

DA IMPARARE

sin(0)=0

sinleft(cfrac{pi}{6}right)=cfrac{1}{2}

sinleft(cfrac{pi}{4}right)=cfrac{sqrt{2}}{2}

sinleft(cfrac{pi}{3}right)=cfrac{sqrt{3}}{2}

sinleft(cfrac{pi}{2}right)=1

sin(pi)=0

sinleft(cfrac{3}{2}piright)=-1

sinleft(2piright)=0

In maniera analoga le seguenti:

cos(0)=1

cosleft(cfrac{pi}{6}right)=cfrac{sqrt{3}}{2}

cosleft(cfrac{pi}{4}right)=cfrac{sqrt{2}}{2}

cosleft(cfrac{pi}{3}right)=cfrac{{1}{2}

cosleft(cfrac{pi}{2}right)=0

cos(pi)=-1

cosleft(cfrac{3}{2}piright)=0

cosleft(2piright)=1

Le formule di addizione permettono lo svolgimento di molti problemi; eccole!

sin(alpha+beta)=sinalphacosbeta+cosalphasinbeta

cos(alpha+beta)=cosalphacosbeta-sinalphasinbeta

Dalla circonferenza goniometrica e dalle formule precedenti posso trovare le seguenti relazioni:

sinleft(cfrac{pi}{2}-alpharight)=cosalpha

sinleft(cfrac{pi}{2}+alpharight)=cosalpha

cosleft(cfrac{pi}{2}-alpharight)=sinalpha

cosleft(cfrac{pi}{2}+alpharight)=-sinalpha

sinleft(pi-alpharight)=sinalpha

sinleft(pi+alpharight)=-sinalpha

cosleft(pi-alpharight)=-cosalpha

cosleft(pi+alpharight)=-cosalpha

sinleft(2pi-alpharight)=-sinalpha

cosleft(2pi-alpharight)=cosalpha

 

 

 

Pubblicato in Uncategorized | Lascia un commento