Registrazione
Categorie
-
Articoli recenti
Commenti recenti
- admin su [:it]Problemi con i numeri relativi[:]
- Mihi su [:it]Problemi con i numeri relativi[:]
- Claudio su Ellisse: formula di sdoppiamento
- Alejandro Zarate su [:it]TPSIT: Test sulla teoria dell’informazione e codici[:]
- Francesco Bragadin su [:it]Raspberry – bridge wifi – ethernet[:]
Meta
Categorie
-
Articoli recenti
Commenti recenti
- admin su [:it]Problemi con i numeri relativi[:]
- Mihi su [:it]Problemi con i numeri relativi[:]
- Claudio su Ellisse: formula di sdoppiamento
- Alejandro Zarate su [:it]TPSIT: Test sulla teoria dell’informazione e codici[:]
- Francesco Bragadin su [:it]Raspberry – bridge wifi – ethernet[:]
Meta
Protetto: Materiale per esame ECDL
Pubblicato in Uncategorized
Inserisci la tua password per visualizzare i commenti.
Esercizi sul M.C.D. e m.c.m tra monomi
Prima di cominciare gli esercizi, preferisco ridefinire il procedimento.
m.c.m. lettere comuni e non comuni con il massimo esponente.
M.C.D. SOLO lettere comuni con l’esponente più basso
Determinare il m.c.m ed il M.C.D. trai seguenti monomi:
1) ![]() ;
; ![]() ;
; ![]()
2) ![]() ;
; ![]() ;
; ![]()
3) ![]() ;
;![]() ;
; ![]()
4) ![]() ;
;![]() ;
; ![]()
5) ![]() ;
; ![]() ;
; ![]()
6) ![]() ;
; ![]() ;
; ![]()
7) ![]() ;
; ![]() ;
; ![]()
8) ![]() ;
; ![]() ;
; ![]()
Pubblicato in Uncategorized
Lascia un commento
Limiti infiniti: asintoto verticale: approfondimento
Nell’introduzione avevo accennato al fatto che studiare cosa accade ad una funzione nell’intorno di un punto significa studiare il limite a destra e a sinistra.Tale studio, com’è consuetudine, in analisi si riassume in tali forme:
(1) ![]()
(2) ![]()
la (1) descrive il fatto che si studia l’andamento della funzione quando ci si avvicina al valore ![]() provenendo da destra.
provenendo da destra.
la (2) descrive il fatto che si studia l’andamento della funzione quando ci si avvicina al valore ![]() provenendo da sinistra.
provenendo da sinistra.
Ad esempio: assumo che ![]() allora provenire da sinistra significa prendere i seguenti valori: 1,8; 1,9; 1,91 e così via; provenire da destra significa prendere i seguenti valori 2,2; 2,1; 2,001 e così via.
allora provenire da sinistra significa prendere i seguenti valori: 1,8; 1,9; 1,91 e così via; provenire da destra significa prendere i seguenti valori 2,2; 2,1; 2,001 e così via.
Ancora provenire da destra significa prendere valori ![]() mentre provenire da sinistra significa prendere valori
mentre provenire da sinistra significa prendere valori ![]() .
.
Per capire se la funzione assume un valore ![]() o
o ![]() si deve studiare il segno della funzione in un intorno del valore a cui tende la
si deve studiare il segno della funzione in un intorno del valore a cui tende la ![]() .
.
Ecco un esempio:
(3) ![]()
(4) ![]()
Infatti:
– il dominio è tutto ![]() escludendo il valore in cui si annulla il denominatore ossia 2.
escludendo il valore in cui si annulla il denominatore ossia 2.
– devo studiare la seguente disequazione:
![]() .
.
Per ![]() la funzione è positiva mentre per
la funzione è positiva mentre per ![]() la funzione è negativa.
la funzione è negativa.
La regola è:
per studiare i limiti nella forma (1) e (2) si deve studiare la disequazione della funzione di cui si deve studiare il limite.
Tale regola giustifica il continuo studio delle disequazioni frazionarie negli anni scolastici precedenti!
Quindi si ha sempre un asintoto verticale ma la funzione ha un andamento diverso.
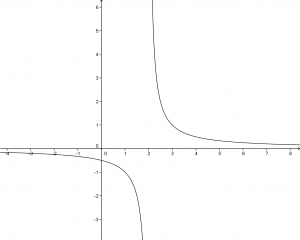
Il grafico della funzione:
![]() è:
è:
Si nota che:
all’avvicinarsi a 2 da destra la funzione assume valori sempre positivi al limite infinitesimamente positivi;
all’avvicinarsi a 2 da sinistra la funzione assume valori sempre negativi al limite infinitesimamente negativi.
Pubblicato in Senza categoria
Lascia un commento
Limiti infiniti – asintoto verticale
Il concetto di infinito lo si affronta solo all’ultimo anno delle superiori come se esso non fosse già ben presente nella quotidianità.
(1) ![]() .
.
(2) ![]() .
.
Per dare un’applicazione pratica immediata si sappia che tale limite permette di definire l’asintoto verticale.
Un asintoto è una retta a cui la funzione di partenza tende ad avvicinarsi senza però mai toccarla: asintoto=senza sintesi ossia privo di unione, nel senso che le curve non si toccano.
Si noi che nella (1) e nella (2) ho fatto uso di ![]() e
e ![]() ossia esiste un infinito positivo ed un infinito negativo: si pensi ai numeri positivi: essi sono infiniti, in senso positivo; mentre quelli negativi sono infiniti in senso negativo.
ossia esiste un infinito positivo ed un infinito negativo: si pensi ai numeri positivi: essi sono infiniti, in senso positivo; mentre quelli negativi sono infiniti in senso negativo.
Per determinare gli asintoti verticali si considerino i punti in cui la funzione non è definita ossia quei punti che sono esclusi dal dominio.
Esempio pratico immediato:
Si consideri la funzione:
![]()
essa è definita per ogni valore di ![]() escluso il punto
escluso il punto ![]() .
.
Studiamo cosa accade un tale punto:
![]()
ossia se si sostituiscono valori sempre più piccoli di ![]() si noti che il valore della funzione assume sempre valori più grandi: al limite, appunto, ci si trova con un numero così grande che sinteticamente viene scritto
si noti che il valore della funzione assume sempre valori più grandi: al limite, appunto, ci si trova con un numero così grande che sinteticamente viene scritto ![]() .
.
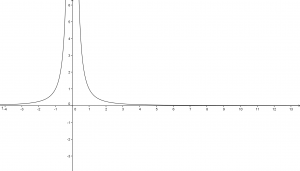
Per completezza e per dare una rappresentazione grafica tale curva, sul piano cartesiano ha il seguente andamento:
Tale curva ha proprio un asintoto verticale coincidente con l’asse delle ordinate.
Pubblicato in Senza categoria
Lascia un commento
Il m.cm. e M.C.D. tra monomi
Prima di affrontarle il mcm e MCD per i monomi è interessante richiamarli dal punto di vista algebrico:
m.c.m: il minimo comune multiplo è il prodotto di tutti i fattori comuni e non comuni presi con il massimo esponente.
M.C.D. il massimo comune divisore invece è il prodotto dei SOLI fattori comuni presi con l’esponente più basso.
Ecco una lezione interessante sul mcm tra monomi:
Ecco una lezione interessante sul M.C.D. tra i monomi
Pubblicato in Uncategorized
Lascia un commento
L’infinito
 In matematica il concetto di infinito procura spesso grandi dubbi esattamente come la più grande poesia di ogni tempo che il genio di Leopardi ci ha regalato:
In matematica il concetto di infinito procura spesso grandi dubbi esattamente come la più grande poesia di ogni tempo che il genio di Leopardi ci ha regalato:
« Sempre caro mi fu quest’ermo colle,
e questa siepe, che da tanta parte
dell’ultimo orizzonte il guardo esclude.
Ma sedendo e mirando, interminati
spazi di là da quella, e sovrumani
silenzi, e profondissima quïete
io nel pensier mi fingo, ove per poco
il cor non si spaura. E come il vento
odo stormir tra queste piante, io quello
infinito silenzio a questa voce
vo comparando: e mi sovvien l’eterno,
e le morte stagioni, e la presente
e viva, e il suon di lei. Così tra questa
immensità s’annega il pensier mio:
e il naufragar m’è dolce in questo mare. »
Tornando però nell’ambito matematico l’infinito è un concetto collegato a quello di asintoto. L’asintoto è una retta immaginaria a cui la funzione cerca di avvicinarsi ma a cui non arriva mai.
E’ come il concetto di velocità della luce: ad essa non ci si può mai arrivare ma solo tendere in quanto per arrivarci bisognerebbe avere una massa infinitamente piccola se non nulla; tale velocità infatti è raggiungibile solo dall’energia!
Pubblicato in Uncategorized
Lascia un commento
I limiti: introduzione
Il concetto di limite è fondamentale per capire verso quale valore tende una funzione. In particolare mi interessa dettare delle regole pratiche per poterne fare un protocollo di attuazione immediata:
Ecco la sua forma più semplice ed immediata:
![]()
Come si legge?
Il limite per ![]() che tende a
che tende a ![]() di
di ![]() vale
vale ![]() .
.
Ho sostituito il valore a cui tende la ![]() nella funzione di partenza.
nella funzione di partenza.
es.1
![]()
In questo caso il valore a cui tende la funzione coincide con il valore stesso della funzione in quel punto. Sembra una tautologia ma in realtà non è così: sia che ci si avvicini da destra che da sinistra a quel punto, il risultato non cambia.
Il concetto di limite destro e sinistro è fondamentale nello studio di funzione: a seconda che ci si avvicini da sinistra o da destra il valore della funzione potrebbe assumere dei valori diversi.
REGOLA PRATICA
Per sviluppare un limite la prima operazione è proprio quella di sostituire il valore a cui tende la ![]() alla funzione.
alla funzione.
Pubblicato in Senza categoria
Lascia un commento
Trigonometria: per esercitarsi sulle formule di addizione: problema 3
3) Dato ![]() che appartengono al primo quadrante e che:
che appartengono al primo quadrante e che:
![]()
![]()
Dimostrare che:
![]()
Sviluppo
(1) ![]()
![]() ossia
ossia
(2) ![]()
Adesso utilizzo la (1)
![Rendered by QuickLaTeX.com tanalpha=cfrac{sinalpha}{cosalpha}=cfrac{sinleft(cfrac[l]{pi}{4}-betaright)}{cosleft(cfrac{pi}{4}-betaright)}=cfrac{sincfrac{pi}{4}cosbeta-sinbetacoscfrac{pi}{4}}{coscfrac{pi}{4}cosbeta+sincfrac{pi}{4}sinbeta}=cfrac{1}{2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a10f0ac6db51364ed3da397a95eb06ba_l3.png)
quindi utilizzando anche la (2) e sviluppando il seno di 45° ed il coseno di 45° ho:
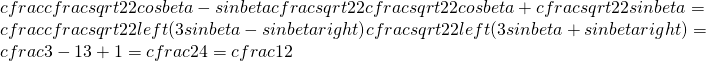
Pubblicato in Uncategorized
Lascia un commento
Trigonometria: per esercitarsi sulle formule di addizione (problema 2)
2) Dato un triangolo i cui angoli ![]() seguono le seguenti relazioni:
seguono le seguenti relazioni:
![]()
![]()
dire se tale triangolo è acutangolo o ottusangolo e determinare ![]() .
.
Sviluppo
Un triangolo si dice acutangolo quando ha tutti e tre gli angoli minori di 90°.
Un triangolo si dice ottusangolo quando un angolo è ottuso ossia maggiore di 90°.
Nel caso specifico ![]() è positivo per cui
è positivo per cui ![]() non potrà mai essere tra
non potrà mai essere tra ![]() perchè la somma degli angoli interni di un triangolo è sempre 180°.
perchè la somma degli angoli interni di un triangolo è sempre 180°.
Lo stesso ragionamento vale per ![]() .
.
Quindi ![]() e non si può ancora dire se il terzo angolo sia maggiore o minore di 90° condizione che ci fa affermare se avere un acutangolo o un ottusangolo.
e non si può ancora dire se il terzo angolo sia maggiore o minore di 90° condizione che ci fa affermare se avere un acutangolo o un ottusangolo.
Allora, sempre per la relazione fondamentale che la somma degli angoli interni di un triangolo è 180°, ![]() .
.
(1) ![]()
Adesso ho:
(2) ![]()
prendo il valore positivo in quanto ![]() .
.
(3) ![]()
prendo il valore positivo in quanto ![]() .
.
Adesso sostituisco i valori dati dal problema e la (2) e la (3) nella (1) e risulta:
![]()
La tangente assume un valore negativo tra ![]()
per cui alla fine mi troverò un ottusangolo!
Pubblicato in Uncategorized
Lascia un commento




 .
.

