1) ![]() .
.
2) ![]() .
.
3) ![]() .
.
4) ![]() .
.
5) 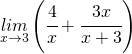 .
.
6) ![]() .
.
7) ![]() .
.
8) ![]() .
.

Prima di affrontarle il mcm e MCD per i monomi è interessante richiamarli dal punto di vista algebrico:
m.c.m: il minimo comune multiplo è il prodotto di tutti i fattori comuni e non comuni presi con il massimo esponente.
M.C.D. il massimo comune divisore invece è il prodotto dei SOLI fattori comuni presi con l’esponente più basso.
Ecco una lezione interessante sul mcm tra monomi:
Ecco una lezione interessante sul M.C.D. tra i monomi
 In matematica il concetto di infinito procura spesso grandi dubbi esattamente come la più grande poesia di ogni tempo che il genio di Leopardi ci ha regalato:
In matematica il concetto di infinito procura spesso grandi dubbi esattamente come la più grande poesia di ogni tempo che il genio di Leopardi ci ha regalato:
« Sempre caro mi fu quest’ermo colle,
e questa siepe, che da tanta parte
dell’ultimo orizzonte il guardo esclude.
Ma sedendo e mirando, interminati
spazi di là da quella, e sovrumani
silenzi, e profondissima quïete
io nel pensier mi fingo, ove per poco
il cor non si spaura. E come il vento
odo stormir tra queste piante, io quello
infinito silenzio a questa voce
vo comparando: e mi sovvien l’eterno,
e le morte stagioni, e la presente
e viva, e il suon di lei. Così tra questa
immensità s’annega il pensier mio:
e il naufragar m’è dolce in questo mare. »
Tornando però nell’ambito matematico l’infinito è un concetto collegato a quello di asintoto. L’asintoto è una retta immaginaria a cui la funzione cerca di avvicinarsi ma a cui non arriva mai.
E’ come il concetto di velocità della luce: ad essa non ci si può mai arrivare ma solo tendere in quanto per arrivarci bisognerebbe avere una massa infinitamente piccola se non nulla; tale velocità infatti è raggiungibile solo dall’energia!
Il concetto di limite è fondamentale per capire verso quale valore tende una funzione. In particolare mi interessa dettare delle regole pratiche per poterne fare un protocollo di attuazione immediata:
Ecco la sua forma più semplice ed immediata:
![]()
Come si legge?
Il limite per ![]() che tende a
che tende a ![]() di
di ![]() vale
vale ![]() .
.
Ho sostituito il valore a cui tende la ![]() nella funzione di partenza.
nella funzione di partenza.
es.1
![]()
In questo caso il valore a cui tende la funzione coincide con il valore stesso della funzione in quel punto. Sembra una tautologia ma in realtà non è così: sia che ci si avvicini da destra che da sinistra a quel punto, il risultato non cambia.
Il concetto di limite destro e sinistro è fondamentale nello studio di funzione: a seconda che ci si avvicini da sinistra o da destra il valore della funzione potrebbe assumere dei valori diversi.
REGOLA PRATICA
Per sviluppare un limite la prima operazione è proprio quella di sostituire il valore a cui tende la ![]() alla funzione.
alla funzione.
3) Dato ![]() che appartengono al primo quadrante e che:
che appartengono al primo quadrante e che:
![]()
![]()
Dimostrare che:
![]()
Sviluppo
(1) ![]()
![]() ossia
ossia
(2) ![]()
Adesso utilizzo la (1)
![Rendered by QuickLaTeX.com tanalpha=cfrac{sinalpha}{cosalpha}=cfrac{sinleft(cfrac[l]{pi}{4}-betaright)}{cosleft(cfrac{pi}{4}-betaright)}=cfrac{sincfrac{pi}{4}cosbeta-sinbetacoscfrac{pi}{4}}{coscfrac{pi}{4}cosbeta+sincfrac{pi}{4}sinbeta}=cfrac{1}{2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a10f0ac6db51364ed3da397a95eb06ba_l3.png)
quindi utilizzando anche la (2) e sviluppando il seno di 45° ed il coseno di 45° ho:
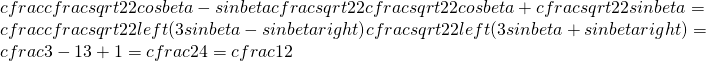
2) Dato un triangolo i cui angoli ![]() seguono le seguenti relazioni:
seguono le seguenti relazioni:
![]()
![]()
dire se tale triangolo è acutangolo o ottusangolo e determinare ![]() .
.
Sviluppo
Un triangolo si dice acutangolo quando ha tutti e tre gli angoli minori di 90°.
Un triangolo si dice ottusangolo quando un angolo è ottuso ossia maggiore di 90°.
Nel caso specifico ![]() è positivo per cui
è positivo per cui ![]() non potrà mai essere tra
non potrà mai essere tra ![]() perchè la somma degli angoli interni di un triangolo è sempre 180°.
perchè la somma degli angoli interni di un triangolo è sempre 180°.
Lo stesso ragionamento vale per ![]() .
.
Quindi ![]() e non si può ancora dire se il terzo angolo sia maggiore o minore di 90° condizione che ci fa affermare se avere un acutangolo o un ottusangolo.
e non si può ancora dire se il terzo angolo sia maggiore o minore di 90° condizione che ci fa affermare se avere un acutangolo o un ottusangolo.
Allora, sempre per la relazione fondamentale che la somma degli angoli interni di un triangolo è 180°, ![]() .
.
(1) ![]()
Adesso ho:
(2) ![]()
prendo il valore positivo in quanto ![]() .
.
(3) ![]()
prendo il valore positivo in quanto ![]() .
.
Adesso sostituisco i valori dati dal problema e la (2) e la (3) nella (1) e risulta:
![]()
La tangente assume un valore negativo tra ![]()
per cui alla fine mi troverò un ottusangolo!
1) Dato un triangolo i cui angoli (![]() ) seguono le seguenti relazioni:
) seguono le seguenti relazioni:
![]() con
con ![]()
![]() con
con ![]()
Determinare il ![]() .
.
Sviluppo:
![]() ossia
ossia
![]()
devo determinare:
(1) ![]()
in cui ho utilizzato le formule di addizione.
siccome in trigonometria vale la relazione fondamentale che è la diretta conseguenza del teorema di Piragora:
![]()
allora
![]()
devo prendere il segno positivo o negativo?
Siccome il ![]() è positivo per
è positivo per ![]() allora prendo il segno positivo ed ho quindi:
allora prendo il segno positivo ed ho quindi:
(2) ![]()
In maniera analoga ho:
![]()
Prendo il segno positivo perchè ![]() è positivo per
è positivo per ![]()
quindi:
(3) ![]()
Adesso sostituisco la (2) e la (3) nella (1) prendendo anche i dati di partenza e risulta:
![]()
razionalizzando (ossia moltiplicando per ![]() sia il numeratore che il denominatore) il risultato conclusivo diventa:
sia il numeratore che il denominatore) il risultato conclusivo diventa:
![]()
Il triangolo di Tartaglia rimane una pietra miliare che indica il passaggio dai più conosciuti prodotti notevoli a quelli meno usati.
Tale post è stato richiesto da un alunno (A.M.O.) che si chiedeva perchè non si potessero avere i prodotti successivi!
Propedeutico è esplicitare tutti gli esponenti dei binomi per apprezzare compeltamente la schematizzazione.
![]()
![]()
adesso se si vuole scrivere l’elevamento a potenza successivo è indispensabile avere il triangolo di Tartaglia:
_______![]() –>
–> ![]()
______![]() –>
–>![]()
_____![]() –>
–>![]()
____![]() –>
–>![]()
___![]() –>
–>![]()
quindi la quarta riga mi fornisce:
![]()
Come si crea il triangolo di Tartaglia?
Ad esempio nella quinta riga il 5 è dato dalla somma dell’1 e del 4 della riga precedente.
Il 10 è dato dalla somma del 4 e del 6 della riga precedente e così via.
Osservando il grafico presente nel post precedente si possono evincere gli angoli fondamentali:
Attenzione però alla seguente notazione:
![]()
![]()
![]()
![]()
In trigonometria si utilizza sempre tale notazione per indicare il valore degli angoli.
DA IMPARARE
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In maniera analoga le seguenti:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Le formule di addizione permettono lo svolgimento di molti problemi; eccole!
![]()
![]()
Dalla circonferenza goniometrica e dalle formule precedenti posso trovare le seguenti relazioni:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
La trigonometria mette in relazione il valore degli angoli di un triangolo rettangolo con i lati.
Le sue applicazioni si possono trovare in astronomia, in fisica, in geologia ed anche nella musica.
Tolomeo è stato il primo a trattare la materia in maniera formale applicandola allo studio teorico della geometria e di tutti i poligoni inscritti in una circonferenza.
Data la seguente figura:
Le relazione che lega il valore dell’angolo al lato è la seguente:
![]()
![]()
un’ulteriore funzione è la seguente:
![]()
A questo punto per meglio immaginare cosa sono il seno ed il coseno è corretto rappresentarli sul piano cartesiano
![]()
![]()
![]() y=tan(x)$
y=tan(x)$