SCIENZE E TECNOLOGIE INFORMATICHE

Il problema presenta tutte le difficoltà di un tipico problema di una maturità scientifica; ottimo banco di prova per il passaggio a facoltà scientifiche.

Ecco la soluzione:

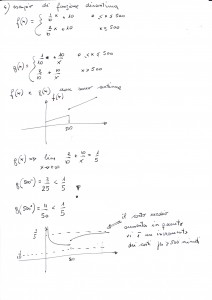
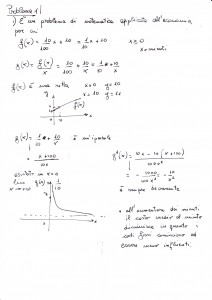Il problema richiedeva una buona capacità di applicazione di media di una funzione e molta praticità nel disegnare semplici curve. Nel complesso fattibile ma complesso per le sue implicazioni pratiche.

Ecco le soluzioni

Un quesito molto complesso dal punto di vista dello studio della probabilità e complesso anche nella fase d’impostazione. Per il suo sviluppo si richiede almeno un modulo di 20 ore sulla probabilità. Indubbiamente fuori portata da parte dei ragazzi.

Un quesito dall’apparenza molto complesso in realtà se analizzato attraverso un semplice triangolo regolare inscritto si poteva arrivare alla conclusione. Ricordarsi le formule di duplicazione trigonometriche e un po’ di trigonometria.

Quesito assolutamente complesso non per lo sviluppo che è banalissimo quanto per il fatto che l’argomento dell’equazione di un piano lo si tratta in maniera molto veloce se non altrimenti lo si tralascia completamente. E’ un argomento di analisi 2 all’università completamente inutile per chi dovesse affrontare una facoltà diversa da ingegneria, matematica  o fisica.

Difficile nell’impostazione delle lettere e nel ricordarsi il prodotto notevole. Lungo nello svolgimento e molta attenzione ai calcoli. Concettualmente molto facile.

Facilissimo in quanto l’integrale da calcolare è tra quelli più banali per un liceo. Le intersezioni erano molto banali.

Quesito facile per chi ha capito il concetto di continuità e derivabilità di una funzione e ha studiato bene il teorema di Lagrange.

Direi veramente molto facile. Semplicissima derivata prima e poi studio del segno di una semplice disequazione di primo grado.

Molto semplice, bastava saper fare la derivata del quoziente di funzione ed aver visto delle semplici equazioni differenziali.