SCIENZE E TECNOLOGIE INFORMATICHE

Attenzione ai segni dei denominatori negli esercizi 1 – 2- 3

1)
2)
3)

4)

5)

Renè Magritte

Gli esercizi sono suddivisi per livello.

Il trucco per risolverle è quello di analizzare prima il denominatore e poi fare il minimo comune multiplo tra i denominatori.

Se al denominatore compaiono numeri e polinomi o monomi, fare il m.c.m. prima dei numeri e poi quello tra i monomi o i polinomi.

Esercizi per un livello sufficiente (6):

6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.
6.11.
6.12.

Per un livello discreto (7)

Renè Magritte, La sera che cade, 1964

Le equazioni razionali frazionarie sono quelle che non hanno l’incognita sotto radice ma hanno l’incognita al denominatore ed al numeratore.

In pratica un’equazione frazionaria (da adeso in poi continuerò a chiamarla cosi)  è del tipo:

(1)  

Si risolve con i normali metodi di un’equazione di primo grado con un’avvertenza: quando si semplifica il denominatore bisogna studiare il dominio entro il quale l’equazione ha soluzione o più banalmente il CAMPO D’ACCETTABILITA’, meglio ancora, i valori consentiti che risolvono l’equazione.

Per arrivare a risolvere l’equazione usata come esempio, preferisco richiamare come si sviluppa un’espressione con soli numeri, con numeri e lettere per poi arrivare a risolvere la (1).

Prendo l’espressione:

essa si sviluppa prendendo il minimo comune multiplo del denominatore ossia

quindi l’espressione diventa:

Adesso prendo l’espressione:

essa si sviluppa prendendo il minimo comune multiplo del denominatore ossia

quindi l’espressione diventa:

Focalizzo l’attenzione sul denominatore ossia perché possa aver senso, A e B dovranno essere sempre diversi da zero altrimenti dividerei qualcosa per zero e ciò è impossibile.

Adesso torno all’equazione di partenza:

(1)  

Faccio il minimo comune multiplo pensando che

A= x-1

e

B=x-2

Quindi l’equazione diventa:

Studiando il C.A. (campo d’accettabilità) devo porre:

e

Fatto questo posso semplificare il denominatore e risolvo una semplice equazione di primo grado:

che ha come soluzione

Video su un’equazione frazionaria:

Equazione frazionaria

Tale Post vuole essere il primo che permetta la preparazione al test INVALSI per la seconda superiore.

Prerequisito la capacità di saper leggere con attenzione una domanda.

Evidenzio le capacità che si richiedono per poter affrontare con una certa sicurezza la prova.

• analisi di un grafico: conoscenza della rappresentazione di un punto sul piano cartesiano.
• essere in grado di risolvere le disequazioni di secondo grado oppure capire il significato di soluzione di una disequazione
• Differenza tra il concetto di necessità e di sufficienza
• Conoscere le figure piane
• Da un problema impostare un’equazione
• Essere in grado di identificare la corrispondenza tra una retta e la sua rappresentazione sul piano cartesiano
• Problema di probabilità classico
• Applicare il teorema di Pitagora a triangoli simili
• Essere in grado di leggere una tabella
• Essere in grado di affrontate con sicurezza le percentuali
• Definizione ed analisi dei numeri irrazionali
• Concetto di media
• Essere in grado di trasportare dei dati dalla forma tabellare alla forma di grafico a torta
• Manualità con le formule
• Analisi delle probabilità in forma complessa
• Conoscere le disequazioni di primo grado
• Manualità con i monomi
• Essere in grado di manipolare le formule dei volumi dei solidi
• Capacità di astrazione delle figure –> molto utile fare disegno tecnico

Ecco la prova

invalsi_matematica_2014-2015_secondaria_seconda

Il problema presenta tutte le difficoltà di un tipico problema di una maturità scientifica; ottimo banco di prova per il passaggio a facoltà scientifiche.

Ecco la soluzione:

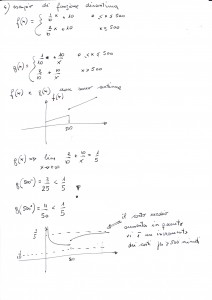
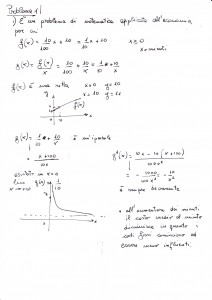Il problema richiedeva una buona capacità di applicazione di media di una funzione e molta praticità nel disegnare semplici curve. Nel complesso fattibile ma complesso per le sue implicazioni pratiche.

Ecco le soluzioni

Un quesito molto complesso dal punto di vista dello studio della probabilità e complesso anche nella fase d’impostazione. Per il suo sviluppo si richiede almeno un modulo di 20 ore sulla probabilità. Indubbiamente fuori portata da parte dei ragazzi.

Un quesito dall’apparenza molto complesso in realtà se analizzato attraverso un semplice triangolo regolare inscritto si poteva arrivare alla conclusione. Ricordarsi le formule di duplicazione trigonometriche e un po’ di trigonometria.

Quesito assolutamente complesso non per lo sviluppo che è banalissimo quanto per il fatto che l’argomento dell’equazione di un piano lo si tratta in maniera molto veloce se non altrimenti lo si tralascia completamente. E’ un argomento di analisi 2 all’università completamente inutile per chi dovesse affrontare una facoltà diversa da ingegneria, matematica  o fisica.