
Hermin Abramovitch
Il teorema di Pitagora si applica SOLO per i triangoli rettangoli:
Il quadrato costruito sull’ipotenusa è uguale al quadrato costruito sui cateti.
in altri termini l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti.
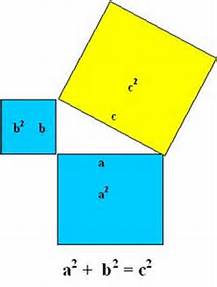 Le sue applicazioni sono infinite in quanto data una figura di qualsiasi forma posso sempre trovare al suo interno un triangolo rettangolo.
Le sue applicazioni sono infinite in quanto data una figura di qualsiasi forma posso sempre trovare al suo interno un triangolo rettangolo.
Le formule che si applicano sono le seguenti:
![]()
dove con
![]() e
e ![]() si indicano i cateti ossia i due lati che formano tra di loro 90° mentre con la lettera
si indicano i cateti ossia i due lati che formano tra di loro 90° mentre con la lettera ![]() si indica l’ipotenusa ossia il lato che unisce gli estremi dei due cateti.
si indica l’ipotenusa ossia il lato che unisce gli estremi dei due cateti.
dalla formula precedente ricavo
- l’ipotenusa dati i due cateti
- un cateto dato l’altro cateto e l’ipotenusa
![]()
![]()
![]()


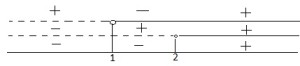 Studio la soluzione:
Studio la soluzione:


![Rendered by QuickLaTeX.com \left [ \left ( -\cfrac{5}{2},0 \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-1714259682fea51bd8142d2c9d4c2a68_l3.png)
![Rendered by QuickLaTeX.com \left [ \left (1,-\cfrac{11}{2} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-4070ae1dfb3cee0078b1bf1e95716d26_l3.png)
![Rendered by QuickLaTeX.com \left [ \left (\cfrac{1}{2},\cfrac{1}{2} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-b68c63f40c33f3afba648ca11672bb77_l3.png)

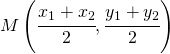

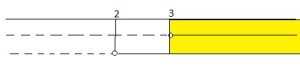 e la soluzione è
e la soluzione è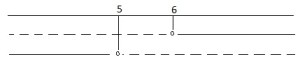 e si nota che la linea continua non si sovrappone mai per cui la soluzione è l’insieme vuoto e si indica appunto:
e si nota che la linea continua non si sovrappone mai per cui la soluzione è l’insieme vuoto e si indica appunto: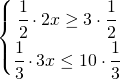
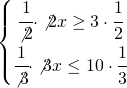
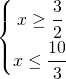
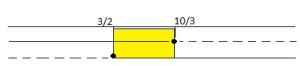 e si nota che la soluzione è compresa tra le due frazioni e si scrive:
e si nota che la soluzione è compresa tra le due frazioni e si scrive: risolvere i sistemi di disequazione è sufficiente essere in grado di risolvere le disequazioni lineari e ricordarsi che la soluzione viene data dalla regione in cui entrambe contemporaneamente risolvono le rispettive disequazioni di partenza.
risolvere i sistemi di disequazione è sufficiente essere in grado di risolvere le disequazioni lineari e ricordarsi che la soluzione viene data dalla regione in cui entrambe contemporaneamente risolvono le rispettive disequazioni di partenza.![Rendered by QuickLaTeX.com \left [ \cfrac{3}{2}\leq x\leq \cfrac{10}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d874d6865e9738e5a0e0a8e1ee9670d1_l3.png)
![Rendered by QuickLaTeX.com \left [ x<\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5fe59560429192c0c5955eed241d455b_l3.png)
![Rendered by QuickLaTeX.com \left [ \cfrac{5}{2}\leq x<\cfrac{7}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-cc102b92e782701a3973533343d93ee5_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{8}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e63eca605efe9170d16822b5d0d2adf2_l3.png)
![Rendered by QuickLaTeX.com \left [ x<-\cfrac{1}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5a3e5d51b7e2a1b42cdda69308d34417_l3.png)
![Rendered by QuickLaTeX.com \left [ -\cfrac{4}{3}<x<\cfrac{5}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-72e747f7aabf492ce7c0ef9261028634_l3.png)
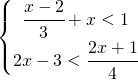
![Rendered by QuickLaTeX.com \left [ x<\cfrac{5}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-96dbd5e87d5edb2f6469946aaa0fb7dc_l3.png)
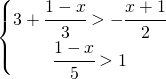
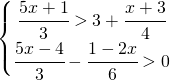
![Rendered by QuickLaTeX.com \left [ x>\cfrac{41}{17}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e549ca2ccebdcab7ea6766e9bb3a5cec_l3.png)
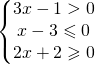 .
.![Rendered by QuickLaTeX.com \left [ \cfrac{1}{3}<x\leqslant 3 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-aee70d4e862ad2e7591477f51a8e5b60_l3.png)
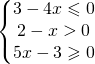
![Rendered by QuickLaTeX.com \left [ \cfrac{3}{4}\leqslant x<2 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-be87c42e4e2f223068cd48943fa66bbe_l3.png)
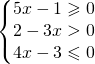
![Rendered by QuickLaTeX.com \left [ \cfrac{1}{5}\leqslant x< \cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d7a4db19a611fb5dcfefdafcdf341945_l3.png)
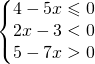
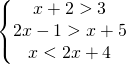
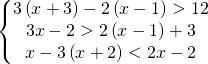
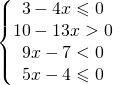
![Rendered by QuickLaTeX.com \left [ \cfrac{3}{4}\leqslant x<\frac{10}{13} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-79634375285228736576b033de4b9385_l3.png)
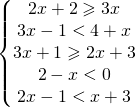
 Tutti i seguenti quiz possono essere affrontati dopo aver compreso come effettuare le derivate, conoscere le disequazioni e le equazioni di primo e secondo grado.
Tutti i seguenti quiz possono essere affrontati dopo aver compreso come effettuare le derivate, conoscere le disequazioni e le equazioni di primo e secondo grado. La probabilità di un evento è la misura del grado di fiducia che una persona ha nel verificarsi dell’evento.
La probabilità di un evento è la misura del grado di fiducia che una persona ha nel verificarsi dell’evento.