SCIENZE E TECNOLOGIE INFORMATICHE

[:it]

Paul David bond

[WpProQuiz 41]

[:]

[:it]Sommare numeri relativi frazionari dignifica applicare comunque tutto ciò che si è appreso con la somma delle frazioni.

Lo richiamo qui con un esempio perché tutta la teoria è presente nel post:

somma tra frazioni

Allora:

Esercizi suddivisi per un livello sufficiente [6]:

6.1.   (+3)+(-5)+(-6)	[-8]
6.2. (+8) + (-10)+(+11)	[+9]
6.3. (-1)+(-3)+(-7)	[-11]
6.4. (-2)+(+7)+(-8)	[-3]
6.5.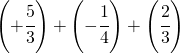
6.6.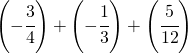
6.7.	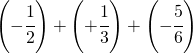[ -1 ]
6.8.	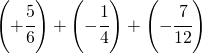[ 0]
6.9.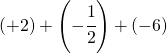
6.10.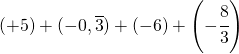
6.11.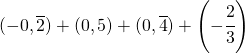
6.12.	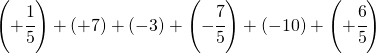[-6]
6.13.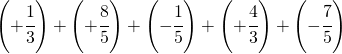
6.14.	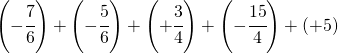[0]
6.15. (+13)+(+32)+(-5)+(-7)+(-10)+(+7)	[+30]
6.16. (-25)+(-10)+(+8)+(+2)+(+4)+(+13)	[-8]
6.17. (15-9)+(11+4-28-9)+(-8+16-11)	[-19]
6.18.	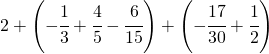[+2]

Si devono eseguire le operazioni a partire da quelle contenute nelle parentesi più interne

Esercizi per un livello discreto [7]:

7.1.	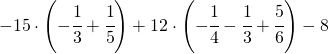[-3]
7.2.	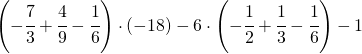[+38]
7.3.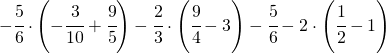
7.4.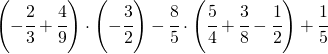
7.5.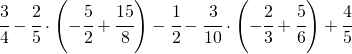

Esercizi per un buon livello [8]

8.1.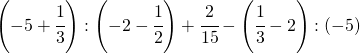
8.2.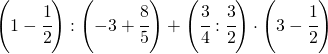
8.3.	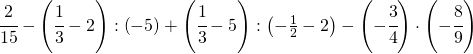[+1]

Esercizi per un ottimo livello [9/10]

10.1.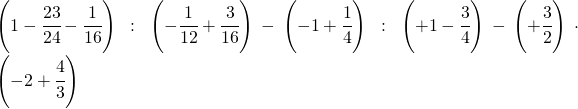

Soluzioni guidate agli esercizi[:]

[:it]

Norman Rockwell

Questo esercizio richiede:

• utilizzo completamento automatico
• utilizzare il simbolo somma
• collegare il valore presente in un foglio con il valore presente in un altro foglio
• inserire un istogramma /grafico
• inserire un grafico a torta
• modificare i colori degli istogrammi

Modulo4esercizio2[:]

[:it]

Norman Rockwell

In questo primo esercizio si deve sapere:

• identificare le celle attraverso le sue coordinate
• unire celle diverse
• sostiutire il contenuto di una cella
• aumentare o diminuire il numero di decimali
• inserire la formula che fornisce la media
• rinominare un foglio

modulo4esercizio[:]

[:it]

Norman Rockwell

Ricordiamoci che i numeri devono essere sempre pensati con il relativo segno.

Per sommare i numeri relativi:

SE DI SEGNO OPPOSTO:

• SI PRENDE IL NUMERO PIU’ GRANDE SENZA IL SEGNO E GLI SI SOTTRAE IL PIU’ PICCOLO
• AL NUMERO RISULTANTE SI METTE IL SEGNO DEL NUMERO PIU’ GRANDE

SE DI SEGNO UGUALE:

• SI SOMMANO I DUE NUMERI SENZA IL SEGNO
• AL NUMERO RISULTANTE SI METTE IL SEGNO DI PARTENZA

Esercizi di base.

Mettere al posto dei puntini il segno opportuno (< minore; > maggiore; = uguale)

A.1. -14…+3
A.2. -15…+15
A.3. +10…-15
A.4. -19…+11
A.5. +3,5 …-26
A.6.
A.7.
A.8.

Determinare, per ciascuna delle seguenti coppie di numeri relativi, qual è il minore:

B.1. -5,+7
B.2.
B.3.
B.4.
B.5.

Completa inserendo opportunamente i simboli > (maggiore), < (minore)

C.1.
C.2.
C.3.
C.4.
C.5.
C.6.

Facendo uso del simbolo < (minore), disporre in ordine crescente i numeri relativi di ciascuno dei seguenti gruppi. Inserire i numeri sull’asse dei nuemri relativi.

D.1. -3; +3; +1; ;

D.2. +2; 0; ; ; ; -4; -1,3; +11,6; -5,4;

[:]

[:it]

Jack Vettriano

[WpProQuiz 40]

[:]

[:it]

Norman Rockwell

Questo metodo si usa quando la derivata seconda mantiene costante il suo segno nell’intervallo entro il quale vi è la soluzione.

Esso si basa sulla determinazione della derivata prima e quindi sulla determinazione della retta tangente nell’estremo la cui ordinata è concorde con la .

La tangente ad una curva in un punto si calcola:

deve è o a seconda che o siano concordi, nell’intervallo, con .

La soluzione è l’intersezione della retta tangente con l’asse delle ascisse per cui si ha:

generalizzando, il procedimento è il seguente:

Il punto di partenza della successione approssimata è l’estremo dell’intervallo in cui la funzione ha lo stesso segno della derivata seconda.

Ci si ferma nella reiterazione quando

è minore della precisione richiesta.

CONCLUSIONE SUI TRE METODI

Si arriva molto velocemente con il metodo delle tangenti ma esso richiede la conoscenza della derivata prima ed anche del segno della derivata seconda.

Con il primo metodo invece non si richiede alcuna derivata ma soltanto un procendimento molto meccanico.

 [:]

[:it]

Norman Rockwell

Per trovare la soluzione in questo caso, invece che trovare il punto medio, come nel metodo di bisezione, si trova la retta passante per i due punti, per cui vale il teorema di unicità della radice, e si determina il suo punto di intersezione con l’asse delle x.

L’errore o approssimazione è data dalla differenza tra le due intersezioni successive ossia:

La retta passante per i due estremi ha equazione:

e la sua intersezione vale:

Ecco il metodo ricorsivo per determinare la soluzione:

Data l’equazione , si cerchi un intervallo tale che .

1. Calcolare
2. Calcolare
3. Se allora è proprio la soluzione e si termina il ciclo altrimenti si va al passo successivo.
4. Solo al passo successivo al primo si calcola , se risulta minore della precisione voluta, si termina il ciclo uscendo.
5. Se si deve scegliere il nuovo intervallo con il seguente criterio:

se allora ,

se allora ,

6. Si torna al punto 1 con i nuovi intervalli.

Nel caso in cui il segno della derivata seconda mantenesse lo stesso segno (ossia la curva mantenesse la stessa concavità) nell’intervallo trovato, il procedimento si semplifica notevolmente e si ha la seguente ricorsione.

Se

allora

Se

allora

 [:]

[:it]

Norman Rockwell

Questo mio approfondimento nasce dall’esigenza di chiarire quando due funzioni logaritmiche sono uguali o meno.

In particolare è corretto affermare che:

?

Se applicassimo la proprietà dei logaritmi senza alcuna riflessione in merito la risposta sarebbe affermativa.

Se andiamo ad effettuare il grafico delle due funzioni ci si accorge che sono uguali solo per .

Allora dove sta la soluzione al problema?

Per applicare la proprietà bisogna prima studiare il dominio ossia scrivere la relazione precedente è possibile farlo solo dopo aver evidenziato che si può fare solo e soltanto per .

Se si fosse richiesto invece di studiare solo la funzione:

allora il dominio sarebbe stato tutto esclusa l’origine.[:]

[:it]Trovare una soluzione non significa che si debba conoscere esattamente il suo valore preciso ma è sufficiente uno approssimato.

Il procedimento si basa sul punto medio di un intervallo, in cui si presuppone esserci una soluzione. La scelta dell’intervallo deve soddisfare il teorema dell’unicità del limite.

Il punto medio si calcola come:

Il valore del punto medio meno la soluzione precisa (che non si conosce) è sicuramente minore di metà dell’intervallo stesso.

Ossia in maniera algebrica:

Quindi si prende metà dell’intervallo, che invece si conosce, come stima dell’approssimazione. Questa scelta assolutamente corretta ha come svantaggio il fatto che, per arrivare all’approssimazione voluta, bisogna reiterare il procedimento numerose volte.

L’approssimazione viene definita come:

Il procedimento si itera prendendo come nuovo estremo dell’intervallo il punto medio trovato e si calcola quindi la nuova media e la nuova stima finchè essa sia minore di quella voluta.

Nei dettagli:

Data l’equazione , si cerchi un intervallo tale che .

1. determinare il punto medio dell’intervallo , , e si calcoli .
2. se , allora è proprio la soluzione e si termina il ciclo altrimenti si va al passo successivo.
3. se allora è un valore approssimato della soluzione e si calcola .
4. Se di quella voluta si esce da ciclo altrimenti si va al passo successivo
5. Si sceglie il nuovo intervallo in questa maniera:

se allora ,

se allora ,

6. si torna torna al numero 1 con in nuovi intervalli.

 [:]