[:it]Test sui monomi[:]

Pubblicato il 12 Maggio 2017 da admin

[:it]

Guido Borelli

[WpProQuiz 49][:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Verifica conclusiva su Power Point e concetti di base sulla teoria dell’informazione[:]

Pubblicato il 10 Maggio 2017 da admin

[:it]

Guido Borelli

13 temi da sviluppare

  1. Tipi di rete LAN, WAN, MAN
  2. Trasmissione a pacchetti
  3. email (SMTP, POP3)
  4. Social Forum
  5. Tutela della salute: illuminazione, corretta postazione di lavoro, ambiente
  6. Sicurezza
  7. Virus
  8. CopyRight
  9. Hardware
  10. software
  11. Firma Digitale
  12. Documenti digitali
  13. Velocità di trasmissione e scaricamento file.

Il power Point dovrà contenere:

  1. Dieci slide
  2. almeno 4 immagini
  3. una diapositiva titolo
  4. una diapositiva Titolo e contenuto
  5. almeno un grafico (a piacere)
  6. almeno 5 forme
  7. almeno una nota per il relatore
  8. il numero di pagina ad esclusione della slide di tipo titolo
  9. la data solo nell’ultima diapositiva
  10. il nome su tutte le diapositive
  11. un indice con il link alle diapositive che lo sviluppano
  12. che ogni slide possa avere una transizione
  13. che ogni slide abbia un’animazione a scelta

[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Approfondimenti Retta sul piano cartesiano in forma parametrica e vettore direzione[:]

Pubblicato il 7 Maggio 2017 da admin

[:it]

Guido Borelli

Normalmente una retta viene sempre definita nella forma

y= mx +q

o nella forma

ax+by+c=0

che viene utilizzata solo quando si deve determinare la distanza tra un punto ed una retta.

Che significato hanno a e b?

Essi rappresentano proprio le componenti del  vettore  v_{\perp }\left ( a;b \right ) perpendicolare alla retta.

Graficamente si vede benissimo tale fatto.

La retta 3x+2y+5=0

ha vettore v_{\perp }\left ( 3;2 \right )

Date due rette

ax+by+c=0

a'x+b'y+c=0

Condizione di parallelismo

Saranno parallele quando i due vettori saranno una combinazione lineare dell’uno rispetto all’altro quindi:

a=\alpha a'

b=\alpha b'

o meglio:

\cfrac{a}{a'}=\cfrac{b}{b'}

graficamente si vede la cosa:

date le rette

2x+2y+5=0

9x+6y+2=0

sono parallele

e si vede che i due vettori sono sovrapposti ed uno è proprio multiplo dell’altro.

Condizione di perpendicolarità

In seguito alla definizione di prodotto scalare tra due vettori, saranno perpendicolari due rette se

a\cdot a'+b\cdot b'=0

Graficamente.

Se si hanno le due rette

2x+2y+5=0 con m_{\perp }(2,2)

9x+6y+2=0 con v_{\perp }(9,6)

Retta in forma parametrica

Tale rappresentazione utilizza il vettore direzione. Vi sono infinite rappresentazione della retta in forma parametrica perché sono infiniti i vettori che sono paralleli ad una retta.

Tale vettore si chiama vettore direzione.

Ad esempio:

\left\{\begin{matrix} x=3+2t\\ y=2+5t \end{matrix}\right.

il vettore direzione ha le coordinate che sono i coefficienti di t

v(2,5)

 

E’ molto più agevole avere la retta in forma parametrica per farne il grafico.

E’ la rappresentazione parametrica della retta

5x-2y-11=0

Passaggio dalla forma parametrica alla forma implicita.

Si risolve il sistema in funzione di t e si confrontano i due valori di t trovati.

Ad esempio:

\left\{\begin{matrix} x=3+2t\\ y=2+5t \end{matrix}\right.

\left\{\begin{matrix} t=\cfrac{x-3}{2}\\ t=\cfrac{y-2}{5} \end{matrix}\right.

\cfrac{x-3}{2}=\cfrac{y-2}{5}

5x-15=2y-4

5x-2y-11=0

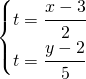
Passaggio dalla forma implicita alla forma parametrica

Vi sono vari metodi.

Uno è il seguente.

La forma implicita

ax+by+d=0

fornisce il vettore  v_{\perp }(a,b), il vettore direzione è perpendicolare a questo per cui avrà coordinate v(b,-a)

La forma parametrica generale è:

\left\{\begin{matrix} x=x_{0}+lt\\ y=y_{0}+mt \end{matrix}\right.

dove v(l,m) è il vettore direzione e P(x_{0},y_{0}) sono le coordinate di un punto appartenente alla retta.

Ad esempio se ho la retta:

x+2y+5=0

il vettore v_{\perp }(1,2), il vettore direzione è v(2,-1),

\left\{\begin{matrix} x=x_{0}+2t\\ y=y_{0}-t \end{matrix}\right.

Adesso prendo il punto P(0,-\cfrac{5}{2}) che appartiene alla retta.

\left\{\begin{matrix} x=0+2t\\ y=-\cfrac{5}{2} -t \end{matrix}\right.[:]

Pubblicato in Senza categoria | Contrassegnato , , | Lascia un commento

[:it]Distanza punto piano[:]

Pubblicato il 7 Maggio 2017 da admin

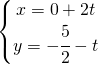[:it]

Cole Rise

La distanza di un punto da un piano non è che la trasposizione nello spazio della distanza di un punto da una retta sul piano cartesiano.

La distanza punto retta sul piano cartesiano

Data la retta nella forma

ax+by+c=0

ed il punto P\left ( x_{p};y_{p} \right )

la distanza sarà:

d=\cfrac{\left | ax_{p}+by_{p}+c \right |}{\sqrt{a^{2}+b^{2}}}

la distanza di un punto nello spazio e di un piano sarà

Dato un piano nella forma

ax+by+cz+d=0

ed il punto P\left ( x_{p};y_{p};z_{p} \right )

la distanza sarà:

d=\cfrac{\left | ax_{p}+by_{p}+cz_{p}+d \right |}{\sqrt{a^{2}+b^{2}+c^{2}}}

 [:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Testo maturità scientifico anno 2015[:]

Pubblicato il 7 Maggio 2017 da admin

[:it]

Guido Borelli

Questi sono i problemi e i quesiti della maturità anno 2015:

matematica-scientifico-problema1

matematica-scientifico-problema2

matematica-scientifico-questionario

 [:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Posizione reciproca tra piani[:]

Pubblicato il 7 Maggio 2017 da admin

[:it]Dati due piani:

ax+by+cz+d=0

a'x+b'y+c'z+d'=0

PIANI PARALLELI

Quando le componenti del vettore v_{\perp } e v'_{\perp } sono uno combinazione lineare dell’altro.

Ossia:

a=\alpha a'

b=\alpha b'

c=\alpha c'

in maniera più compatta e semplice:

\cfrac{a}{a'}=\cfrac{b}{b'}=\cfrac{c}{c'}

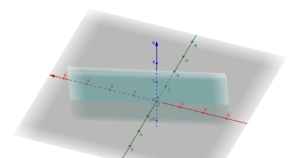
Ad esempio i piani:

2x-6y+4z+1=0

4x-13y+8z+1=0

sono paralleli come si vede nel grafico:

PIANI PERPENDICOLARI

Quando il prodotto scalare dei vettori v_{\perp } e v'_{\perp } è nullo.

Il prodotto scalare è:

\vec{a}\cdot \vec{b}=\left | \vec{a} \right |\cdot \left | \vec{b} \right |\cdot \cos \vartheta

quando sono perpendicolari \cos \vartheta=0

e quindi la condizione è

a\cdot a'+b\cdot b'+c\cdot c'=0

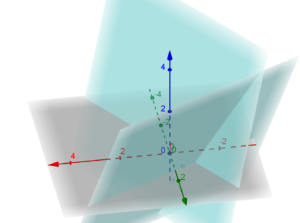
Ad esempio i piani

2x-4y+2z+5=0

3x+2y+z+1=0

sono perpendicolari infatti

2\cdot 3 -4 \cdot 2 + 2 \cdot 1 =0

e graficamente

 [:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Piano[:]

Pubblicato il 6 Maggio 2017 da admin

[:it]Un piano nello spazio ha la seguente equazione:

ax+by+cz+d=0

i coefficienti a, b e c rappresentano le coordinate del vettore perpendicolare al piano.

Ad esempio la rappresentazione del piano 2x+3y+4z+5=0 ha come vettore v_{\perp }\left ( 2,3,4 \right ) è un vettore che è perpendicolare la piano dato.

Graficamente si ha la seguente situazione:

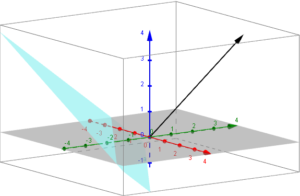
in cui in azzurro si nota il piano ed in grigio il vettore che è proporio perpendicolare al piano in esempio con le coordinate precedentemente date.

Tale affermazione è molto utile quando si devono studiare le posizioni reciproche tra un piano ed una retta.

PIANO PASSANTE PER TRE PUNTI

Un piano è sempre identificato da tre punti per cui, se fossero dati e si dovesse trovare il relativo piano che li contiene, è sufficente sostituire le loro coordinate nell’equazione generica del piano e risolvere il relativo sistema.

Vi è una particolarità: ci si troverà un sistema di tre equazioni in quattro incognite. Lo si risolve come se vi fossero tre incognite, la quarta verrà poi eliminata quando si andranno a sostituire i valori nel piano di partenza.

Ad esempio trovare l’equazione del piano passante per questi tre punti

A(1,1,0) B(0,-3,1) C(2,-2,0)

sostituendo le coordinate nell’equazione generica del piano ho:

\left\{\begin{matrix} a+d=0\\ -3b+c+d=0\\ 2a-2b+d=0 \end{matrix}\right.

\left\{\begin{matrix} d=-a\\ -3b+c-a=0\\ 2a-2b-a=0 \end{matrix}\right.

\left\{\begin{matrix} d=-a\\ c=a+3b\\ a-2b=0 \end{matrix}\right.

\left\{\begin{matrix} d=-2b\\ c=5b\\ a=2b \end{matrix}\right.

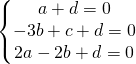
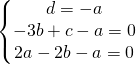
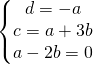
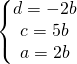
L’equazione del piano diventa:

2bx+by+5bz-2b=0

Ora divido tutto per b e l’equazione del piano diventa:

2x+y+5z-2=0.[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Esercizi multipli power point[:]

Pubblicato il 21 Aprile 2017 da admin

[:it]Questo file fa riferimento all’inserimento di immagini che possono essere trovati on line.

esercizi_ppt[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Probabilità: scommesse[:]

Pubblicato il 31 Marzo 2017 da admin

[:it]

Alex Alemany

Si immagini di trovarsi in questa situazione

La vincita del campionato delle seguenti squadre viene data seguendo la seguente tabella:

Milan 1:5
Inter 1:7
Juve 1:3

ossia:

se una persona scommette 1€ sulla vittoria del campionato del Milan guadagnerà 5€,

se scommette 1€ sulla vittoria del campionato dell’Inter guadagnerà 7€,

se scommet 1€ sulla vittoria del campionato della Juve guadagnerà 3€.

Vi sono due soggetti in questa situazione

  • lo scommettitore che deve conoscere la probabilità di vincita
  • il bookmaker che accetta e fissa le scommesse e non deve perderci anzi guadagnarsi

Conoscere il meccanismo probabilistico è necessario per capire se vale la pena giocare (non convine mai, alla lunga si perde sempre) e se vale la pena fare il bookmaker senza andare in fallimento!

Il ragionamento da cui si deve partire è il seguente:

la probabilità che esca testa è \cfrac{1}{2}

la probabilità che esca croce è \cfrac{1}{2}

allora il bookmaker mette le seguenti quote

1: 2 se esce testa

1:2 se esce croce

in questa maniera però il bookmaker alla fine della giornata di scommesse non avrà guadagnato nulla perchè la somma della probabilità di vincere mi dà l’evento certo ossia l’1.

NOTARE

la probabilità che esca testa vale \cfrac{1}{2} se e solo se si ha un limite infinito di lanci!

Per aver la probabilità in un numero finito di lanci bisogna parlare di distribuzioni di probabilità.

Allora per garantire il guadagno il bookmaker fissa le seguenti quote:

1:1.6 se esce testa ossia se scommetto 1€ ne guadagnerò 1€ e 60 centesimi.

1:1.5 se esce croce ossia se scommetto 1€ ne guadagnerò 1€ e 50 centesimi.

Naturalmente un bookmaker cercherà di evitare di esplicitare in maniera troppo evidente il suo guadagno e lo scommettitore deve stare attento alle probabilità di vincita.

Per capire la vera probabilità degli eventi partendo dalla quote del bookmaker si devono eseguire i seguenti calcoli:

Probabilità che esca testa per il bookmaker–> P[testa]=\cfrac{1}{1.6}=0,625

Probabilità che esca croce per il bookmaker –>P[croce]=\cfrac{1}{1.5}=0,6

Sommo le probabilità e noto che 0,625+0,6=1,3 circa

ossia il bookmaker ha la certezza di guadagnare!

Per capire la probabilità reale che esca testa si dovrà prendere la probabilità che esca testa per il bookmaker e dividerla per la probabilità complessiva del bookmaker (1,3).

Ossia:

0.625:1,3=0,5

La probabilità che esca croce sarà

0.6:1,3=05

che già si sapevano nel caso del lancio delle monete.

Analizzando adesso il problema delle tre squadre di partenza il bookmaker ha garantito il suo guadagno? Qual è la probabilità che vinca il campionato, secondo le quote associate, la relativa squadra?[:]

Pubblicato in Senza categoria | Lascia un commento

[:it]Rette nello spazio: posizioni reciproche[:]

Pubblicato il 31 Marzo 2017 da admin

[:it]

Samy Charnine

Parallelismo

Due rette nello spazio saranno parallele quando

dati i due vettori direzione v(a,b,c) e v'(a’,b’,c’),

il rango della matrice

\begin{pmatrix} a & b & c\\ a' & b' & c'\\ \end{pmatrix}

risulta 1.

Per determinare il rango di una matrice devo prendere la sottomatrice quadrata più grande e verificare se il suo determinante è diverso da 0.

Ossia se due rette sono parallele un vettore direttrice e una combinazione lineare dell’altro.

Perpendicolarità

Due rette sono perpendicolari quando,

dati i due vettori direzione v(a,b,c) e v'(a’,b’,c’),

aa’+bb’+cc’=0

Complanarità

Due rette sono complanari quando sono parallele ed incidenti.[:]

Pubblicato in Senza categoria | Lascia un commento