1) Dato un triangolo i cui angoli (![]() ) seguono le seguenti relazioni:
) seguono le seguenti relazioni:
![]() con
con ![]()
![]() con
con ![]()
Determinare il ![]() .
.
Sviluppo:
![]() ossia
ossia
![]()
devo determinare:
(1) ![]()
in cui ho utilizzato le formule di addizione.
siccome in trigonometria vale la relazione fondamentale che è la diretta conseguenza del teorema di Piragora:
![]()
allora
![]()
devo prendere il segno positivo o negativo?
Siccome il ![]() è positivo per
è positivo per ![]() allora prendo il segno positivo ed ho quindi:
allora prendo il segno positivo ed ho quindi:
(2) ![]()
In maniera analoga ho:
![]()
Prendo il segno positivo perchè ![]() è positivo per
è positivo per ![]()
quindi:
(3) ![]()
Adesso sostituisco la (2) e la (3) nella (1) prendendo anche i dati di partenza e risulta:
![]()
razionalizzando (ossia moltiplicando per ![]() sia il numeratore che il denominatore) il risultato conclusivo diventa:
sia il numeratore che il denominatore) il risultato conclusivo diventa:
![]()



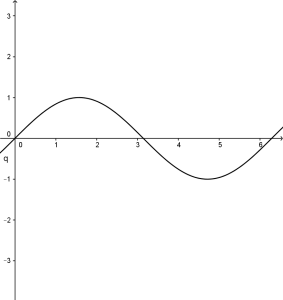
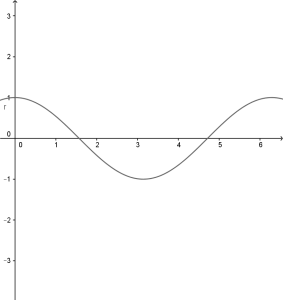

 Una volta che si riesce a calcolare la derivata prima di una funzione si può cominciare ad intuire come potrà essere il suo grafico. In particolare siccome la derivata prima fornisce il valore dell’inclinazione della curva tangente si può capire che quando essa si annulla la relativa retta è orizzontale.
Una volta che si riesce a calcolare la derivata prima di una funzione si può cominciare ad intuire come potrà essere il suo grafico. In particolare siccome la derivata prima fornisce il valore dell’inclinazione della curva tangente si può capire che quando essa si annulla la relativa retta è orizzontale.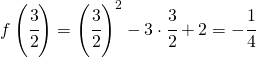
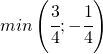
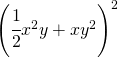 .
.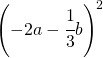 .
.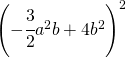 .
.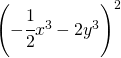 .
.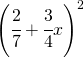 .
.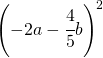 .
.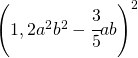 .
. .
. .
.

![Rendered by QuickLaTeX.com \left [y^{'}=-\cfrac{1}{x^2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-95d7e93f5fef6dffb7a19e2f44222eca_l3.png)
 .
.