Jacek Yerka
Un paradosso è una frase o un pensiero logico che sembra in contraddizione con il pensiero comune.
Il paradosso più conosciuto è quello di Zenone (filosofo greco del V secolo a.C.)
Eccolo:
Se Achille (detto “pie’ veloce”) venisse sfidato da una tartaruga nella corsa e concedesse alla tartaruga un piede di vantaggio, egli non riuscirebbe mai a raggiungerla, dato che Achille dovrebbe prima raggiungere la posizione occupata precedentemente dalla tartaruga che, nel frattempo, sarà avanzata raggiungendo una nuova posizione che la farà essere ancora in vantaggio; quando poi Achille raggiungerà quella posizione nuovamente la tartaruga sarà avanzata precedendolo ancora. Questo stesso discorso si può ripetere per tutte le posizioni successivamente occupate dalla tartaruga e così la distanza tra Achille e la lenta tartaruga pur riducendosi verso l’infinitamente piccolo non arriverà mai ad essere pari a zero.
Per meglio capire il paradosso si osservi la seguente figura:
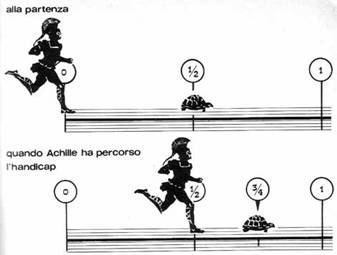Ossia si consideri che:
- Achille vada ad una velocità doppia di quella della tartaruga
- la tartaruga parta con mezzo metro di vantaggio rispetto Achille.
- che si cerchi di capire se entrambi raggiungono il metro da percorrere.
Si può dimostrare che Zenone sbagliava in due maniere:
- attraverso le nozioni fisica ed in particolare utilizzando la descrizione del moto rettilineo uniforme
- attraverso la convergenza della serie numerica.
Dimostrazione mediante la convergenza della serie numerica.
- la tartaruga andando ad una velocità che è metà di quella di Achille percorre sempre metà spazio rispetto a quella che percorre Achille.
Achille all’inizio percorre:
la tartaruga intanto, nello stesso tempo, si è spostata percorrendo:
Achille arriva al punto della tartaruga precedente mentre la tartaruga ha percorso
questo perché la tartaruga percorre sempre la metà del percorso fatto da Achille.
Si ha quindi la seguente tabella che schematizza la strada di Achille e quella della tartaruga:
| Achille | Tartaruga | |
| Tempo 0 0 | |
|
| Tempo 1 |
|
|
Tempo 2  |
|
Quindi per Achille si ha la seguente serie numerica:
che si può dimostrare che tende ad 1!
analogamente la formula precedente descrive la strada percorsa dalla tartaruga che anch’essa converge ad 1.
Quindi l’errore di Zenone è quello di non considerare che la somma infinita di cifre più piccole di 1 converge ad 1! E quindi Achille raggiunge la tartaruga.