[:it]

Alex Alemany
Dati i punti ![]() , determinare l’equazione della retta
, determinare l’equazione della retta ![]() passante per
passante per ![]() e per
e per ![]() e l’equazione del piano
e l’equazione del piano ![]() perpendicolare ad
perpendicolare ad ![]() e passante
e passante ![]() .
.
Prerequisiti
- conoscere l’equazione della retta passante per due punti nello spazio
- capire il significato dei coefficienti numerici della retta e di un piano
- capire il significato di un punto appartenente ad una curva
Sviluppo
L’equazione di una retta passante per due punti ha equazione:
(1) 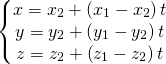
Applicandola al caso posto dal quesito, la retta passante per ![]() e per
e per ![]() ha equazione:
ha equazione:
(2) 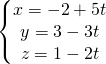
i coefficienti di ![]() (5), di
(5), di ![]() (-3), di
(-3), di ![]() (-2), rappresentano le coordinate del vettore direzione
(-2), rappresentano le coordinate del vettore direzione ![]() ossia quello parallelo alla retta.
ossia quello parallelo alla retta.
L’equazione generale di un piano ha equazione:
(3) ![]()
i coefficienti ![]() ,
,![]() e
e ![]() rappresentano le coordinate del vettore perpendicolare al piano.
rappresentano le coordinate del vettore perpendicolare al piano.
Conseguenza di questo l’equazione del piano ![]() utilizza le coordinate della retta:
utilizza le coordinate della retta:
(4) ![]()
Per trovare ![]() è sufficiente sostituire le coordinate del punto
è sufficiente sostituire le coordinate del punto ![]() e risolvere la relativa equazione di primo grado in d:
e risolvere la relativa equazione di primo grado in d:
(5) ![]()
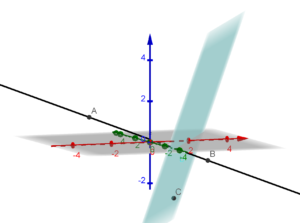
L’equazione del piano risulta:
(6) ![]()
 [:]
[:]
