Parlare di RAID significa parlare di continuità di servizio, significa cercare di limitare gli INEVITABILI malfunzionamenti di un sistema a causa del normale ciclo di vita dei componenti. RAID è acronimo di Redundant Array of Independent Disks.
La tecnologia RAID nasce per effettuare la copia o il controllo degli errori degli hard disk presenti in un host o in un server. A seconda del tipo di controllo o di ridondanza si parla di varie tipologie di RAID.
Le modalità più diffuse sono RAID 0, 1, 5 e 10. La 3 e la 4 sono state praticamente soppiantate dalla 5. Alcuni sistemi usano modalità nidificate come la 10 o altre modalità proprietarie.
RAID 0
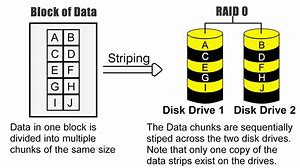
Divide i dati equamente tra due o più dischi, tipicamente tramite sezionamento (o striping), ma senza mantenere alcuna informazione di parità o ridondanza che aumenti l’affidabilità (la dicitura RAID, ancorché diffusa, è pertanto impropria). RAID 0 è usato generalmente per aumentare le prestazioni di un sistema, o per la comodità di usare un grande numero di piccoli dischi fisici come se fossero un piccolo numero di grandi dischi virtuali.
Vantaggi costo di implementazione basso; alte prestazioni in scrittura e lettura, grazie al parallelismo delle operazioni I/O dei dischi concatenati.
Svantaggi impossibilità d’utilizzo di dischi hot-spare (il disco hot-spare viene lasciato dormiente fino al momento di un guasto degli altri dischi) ; affidabilità drasticamente ridotta, anche rispetto a quella di un disco singolo.
FONDAMENTALE
Raid 0 significa che i dati vengono sezionati e scritti su dischi diversi. La rottura del disco farà sì che i dati presenti in quel disco si perdano mentre rimangono quelli dell’altro disco.
RAID 1
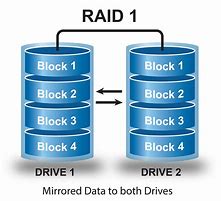
detta anche mirror, mantiene una copia esatta di tutti i dati su almeno due dischi.
È utile quando la ridondanza sia ritenuta un’esigenza più importante rispetto allo sfruttamento ottimale della capacità di memorizzazione dei dischi.
L’insieme, infatti, limita il suo volume a quello del disco di taglia inferiore. D’altro canto, visto che un sistema con n dischi è in grado di resistere alla rottura di n-( “n”-1 ) componenti, l’affidabilità aumenta linearmente al numero di dischi presenti.
A livello prestazionale, il sistema RAID 1 aumenta tipicamente i risultati per le operazioni di lettura, perché molte implementazioni sono in grado di effettuare diverse operazioni in parallelo: mentre la lettura di un blocco è ancora in corso su un disco, cioè, possono effettuarne un’altra su un disco diverso.
In ogni caso, la velocità di lettura raggiunge quella del disco più veloce in presenza di dispositivi di memorizzazione con prestazioni diverse: una singola operazione di lettura è richiesta inizialmente e contemporaneamente su tutti i dischi, ma si conclude nel momento della prima risposta ricevuta.
Viceversa, la velocità di scrittura scende a quella del disco più lento, perché questo tipo di azione richiede il compimento della replica della stessa operazione su ogni disco dell’insieme.
Vantaggi affidabilità, cioè resistenza ai guasti, che aumenta linearmente con il numero di copie; velocità di lettura (in certe implementazioni e sotto certe condizioni).
Svantaggi bassa scalabilità; costi aumentati linearmente con il numero di copie; velocità di scrittura ridotta a quella del disco più lento dell’insieme.
RAID 2
Divide i dati al livello di bit (invece che di blocco) e usa un codice di Hamming per la correzione d’errore che permette di correggere errori su singoli bit e di rilevare errori doppi.
Questi dischi sono sincronizzati dal controllore, in modo tale che la testina di ciascun disco sia nella stessa posizione in ogni disco. Questo sistema si rivela molto efficiente in ambienti in cui si verificano numerosi errori di lettura o scrittura, ma in ambienti più prestanti, data l’elevata affidabilità dei dischi, il RAID 2 non viene utilizzato
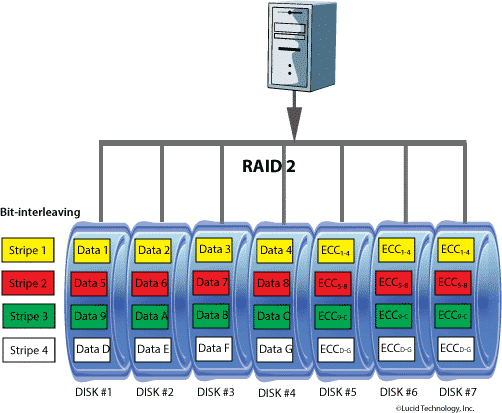
Si notino quindi la presenza di sette dischi esattamente come il codice di Hamming (7,4) studiato. Con stripe si intende il singolo bit.
Il numero minimo di dischi è 7.
RAID 3
Usa una divisione al livello di byte con un disco dedicato alla parità.
Il RAID-3 è estremamente raro nella pratica.
Uno degli effetti collaterali del RAID-3 è che non può eseguire richieste multiple simultaneamente. Questo perché ogni singolo blocco di dati ha la propria definizione diffusa tra tutti i dischi del RAID e risiederà nella stessa posizione, così ogni operazione di I/O richiede di usare tutti i dischi.
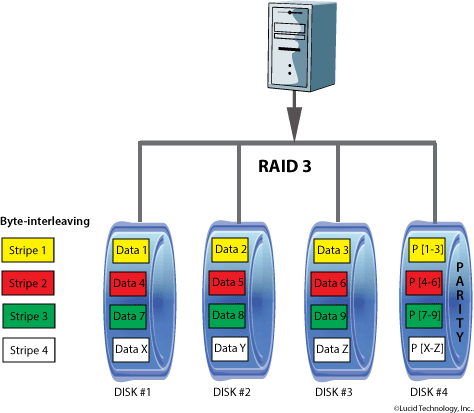
Con stripe si intende un byte. Il byte è generato nella fase di scrittura, memorizzato nel disco di parità e ricontrollato in fase di lettura.
Il numero minimo di dischi è 3:
utilizza un minimo di due dischi per i dati, più un disco dedicato alla memorizzazione dei Byte di parità.
Le prestazioni in scrittura peggiorano, poiché per ogni operazione eseguita sui dati necessita del calcolo della parità, da scrivere sul disco dedicato a questa funzione.
Inoltre, poiché il disco dedicato alla parità è unico, questo costituisce anche una specie di collo di bottiglia che può limitare ulteriormente le prestazioni in scrittura (infatti mentre i dati sono scritti su vari dischi, la parità viene scritta, per ogni operazione di scrittura, sempre sullo stesso disco).
Per assurdo, aumentando i dischi, le prestazioni in lettura migliorano e quelle in scrittura possono addirittura peggiorare.
In caso di guasto, si accede al disco di parità e i dati vengono ricostruiti.
Si utilizza XOR
Una volta che il disco guasto viene rimpiazzato, i dati mancanti possono essere ripristinati e l’operazione può riprendere. La ricostruzione dei dati è piuttosto semplice. Si consideri un array di 5 dischi nel quale i dati sono contenuti nei dischi X0, X1, X2 e X3 mentre X4 rappresenta il disco di parità.
La parità per l’i-esimo bit viene calcolata come segue:
X4(i) = X3(i) ⊕ X2(i) ⊕ X1(i) ⊕ X0(i)
Si supponga che il guasto interessi X1.
Se eseguiamo l’OR esclusivo di X4(i) ⊕ X1(i) con entrambi i membri della precedente equazione otteniamo: X1(i) = X4(i) ⊕ X3(i) ⊕ X2(i) ⊕ X0(i)
Così, i contenuti della striscia di dati su X1 possono essere ripristinati dai contenuti delle strisce corrispondenti sugli altri dischi dell’array.
Questo principio persiste nei livelli RAID superiori.
RAID 4
Usa una divisione dei dati a livello di blocchi e mantiene su uno dei dischi i valori di parità, in maniera molto simile al RAID 3, dove la suddivisione è a livello di byte. Questo permette ad ogni disco appartenente al sistema di operare in maniera indipendente quando è richiesto un singolo blocco.
Se il controllore del disco lo permette, un sistema RAID 4 può servire diverse richieste di lettura contemporaneamente. In lettura la capacità di trasferimento è paragonabile al RAID 0, ma la scrittura è penalizzata, perché la scrittura di ogni blocco comporta anche la lettura del valore di parità corrispondente e il suo aggiornamento.
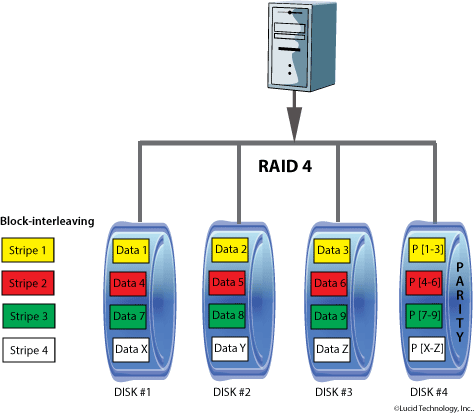
Il RAID 4 utilizza la tecnica dello striping e per la sicurezza utilizza la tecnica del controllo di parità.
E’ in pratica la stessa configurazione del RAID 3, con la differenza che lo striping viene eseguito a livello di blocchi e non di singoli Byte.
Allo stesso modo il calcolo della parità viene eseguito a livello di blocco e scritto di conseguenza.
RAID 5
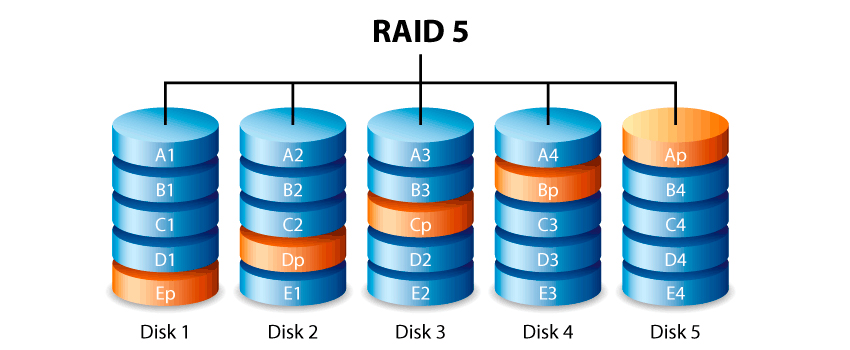
Un sistema RAID 5 usa una suddivisione dei dati a livello di blocco, distribuendo i dati di parità uniformemente tra tutti i dischi che lo compongono. È una delle implementazioni più popolari, sia in software, sia in hardware, dove praticamente ogni dispositivo integrato di storage dispone del RAID-5 tra le sue opzioni.
La differenza fondamentale, che lo distingue dal RAID 4, è che in questa configurazione non esiste il disco dedicato alla scrittura della parità, ma su tutti i dischi vengono scritti indifferentemente i dati o il corrispondente calcolo di parità.
N.B.: la parità viene comunque scritta su disco diverso da quello dei dati, altrimenti il checksum non avrebbe senso; in pratica il blocco di parità viene trattato come un blocco dati qualsiasi e distribuito su un disco qualsiasi.
Non si ha vantaggio in termini di spazio occupato dalla parità, in quanto lo spazio totale “sottratto” ai dati risulta essere sempre l’equivalente di un disco, ma si ottiene un miglioramento delle prestazioni in fase di scrittura eliminando il percorso obbligato, su unico disco, per la scrittura della parità.
Per questo motivo è forse la più popolare delle configurazioni RAID in striping, tenendo anche conto che alcune MB avanzate implementano controller con il supporto RAID 5.
Per la ricostruzione dei dati in caso di guasto del disco, valgono le stesse considerazioni del RAID 3.
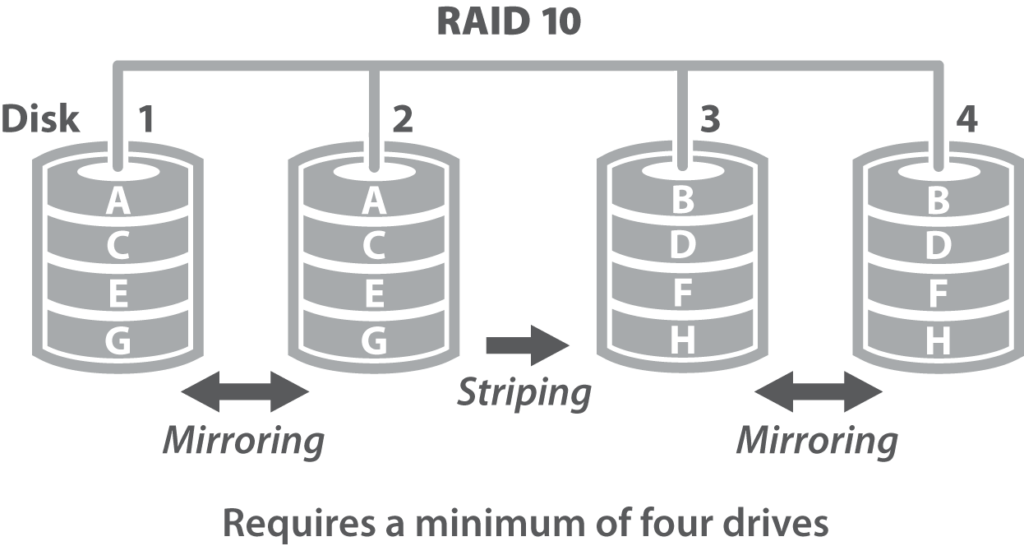
RAID 10
Un sistema RAID 1+0, chiamato anche RAID 10 i livelli RAID sono usati in senso invertito.
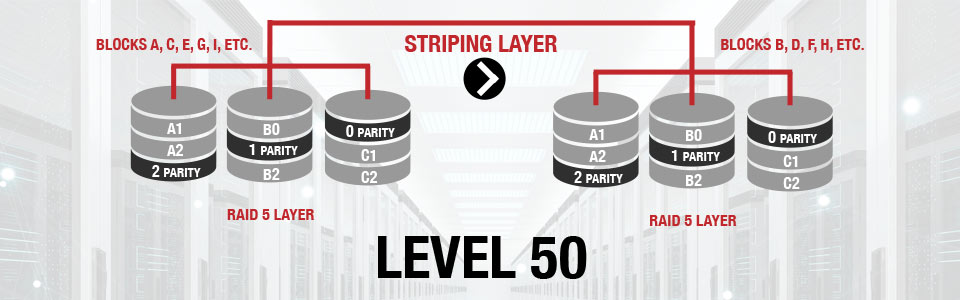
RAID 50