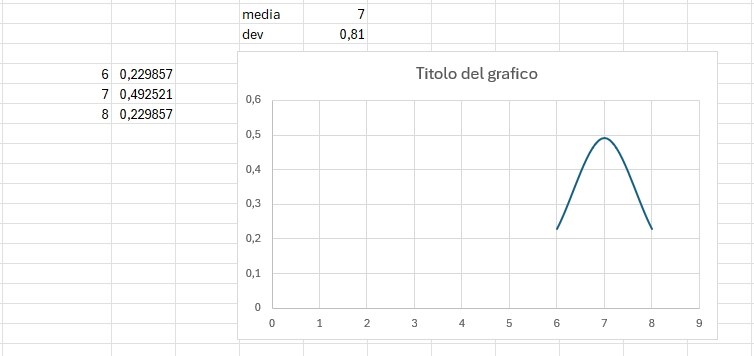
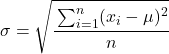Se si vogliono usare le tabelle i comandi base sono i seguenti:
- <table>: definisce la tabella
- <tr> (table row): definisce una riga
- <td> (table data): definisce una cella
ogni singolo tag deve poi essere opportunamente chiuso </table>, </tr>,</td>
Gli attributi al tag table sono:
- border: specifica la larghezza dei bordi di una tabella
- cellspacing: specifica la distanza tra una cella e l’altra, oppure tra una cella e il bordo.
- cellpadding: indica la distanza tra il contenuto della cella e il
bordo.
Gli attributi del tag tr sono:
align: specifica l’allineamento del contenuto (left,center,right)bgcolor:definisce il colore di sfondo della rigavalign: specifica l’allineamento verticale (top,middle,bottom)
Gli attributo del tag td:
colspan: specifica il numero di colonne che la cella deve occupare.rowspan: specifica il numero di righe che la cella deve occupare.align:allinea il contenuto (left,center,right,justify).valign: specifica l’allineamento verticale (top,middle,bottom).bgcolor:definisce il colore di sfondo della cella.width:definisce la larghezza della cella.height:definisce l’altezza della cella.
Ad esempio si può scrivere il seguente codice essenziale
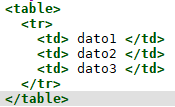
Per avere il risultato dell’immagine precedente si usa l’attributo colspan=4 nel tag <th> e l’attributo rowspan=2 nel tab td.
Ultima nota per usare l’intestazione della tabella si usa il tag <th> con il relativo tag di chiusura </th>