1) ![]()
2) l’unica difficoltà è trasformare in frazione i numeri decimali
![]()

[:it]
Ecco di seguito le soluzioni degli esercizi:
Esercizio 6.1.
![]()
![]()
![]()
![]()
___
Esercizio 6.2
![]()
![]()
![]()
___
Esercizio 6.3
![]()
![]()
![]()
___
Esercizio 6.4
![]()
![]()
![]()
___
Esercizio 6.5
![]()
![]()
![]()
![]()
___
Esercizio 6.6
![]()
![]()
![]()
___
Esercizio 6.7
![]()
![]()
![]()
___
Esercizio 6.8
![]()
![]()
![]()
___
Esercizio 6.9
![]()
![]()
![]()
![]()
___
Esercizio 6.10
![]()
![]()
![]() [:en]
[:en]
Ecco di seguito le soluzioni degli esercizi:
Esercizio 1.
![]()
![]()
![]()
![]()
___
Esercizio 2
![]()
![]()
![]()
___
Esercizio 3
![]()
![]()
![]()
___
Esercizio 4
![]()
![]()
![]()
___
Esercizio 5
![]()
![]()
![]()
![]()
___
Esercizio 6
![]()
![]()
![]()
___
Esercizio 7
![]()
![]()
![]()
___
Esercizio 8
![]()
![]()
![]()
___
Esercizio 9
![]()
![]()
![]()
![]()
___
Esercizio 10
![]()
![]()
![]() [:de]
[:de]
Ecco di seguito le soluzioni degli esercizi:
Esercizio 1.
![]()
![]()
![]()
![]()
___
Esercizio 2
![]()
![]()
![]()
___
Esercizio 3
![]()
![]()
![]()
___
Esercizio 4
![]()
![]()
![]()
___
Esercizio 5
![]()
![]()
![]()
![]()
___
Esercizio 6
![]()
![]()
![]()
___
Esercizio 7
![]()
![]()
![]()
___
Esercizio 8
![]()
![]()
![]()
___
Esercizio 9
![]()
![]()
![]()
![]()
___
Esercizio 10
![]()
![]()
![]() [:]
[:]
Per essere in grado di sviluppare lo studio di funzione è molto utile seguire il seguente protocollo che vuole essere una guida in passi per arrivare al grafico finale.
1- Definire il dominio
2- Scrivere il segno della funzione
3- Verifica della presenza di asintoti verticali, orizzontali, obliqui attraverso i relativi limiti.
4- Determinazione dei massimi e minimi attraverso lo studio della derivata prima: annullamento della derivata prima mi fornisce l’ascissa dei punti di massimo o minimo relativi mentre lo studio della disequazione mi indica se effettivamente vi è un massimo o minimo e se è un massimo o minimo.
5- intersezioni con gli assi
CONCLUSIONE Grafico della funzione.
Per fare il grafico si seguano i seguenti passi.
1 – segnare i punti di massimo o minimo
2- segnare i punti di intersezione
3- disegnare con una linea tratteggiata gli eventuali asintoti
4- tracciare il grafico seguendo le indicazioni fornite da tutti i punti precedenti
Possono essere risolti con le metodologie che si ritengono più opportune.Per risolvere un limite comunque si deve cercare di sostituire il valore a cui tende la x all’interno della funzione, dopo si scegli la strada più opportuna.
(1) ![]() .
.
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
(8) 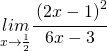
(9) ![]()
(10) ![]()
(11) ![]()
(12) ![]()
(13) ![]()
(14) ![]()
(15) ![]()
La regola di De L’Hospital è utilissima nel calcolo dei limiti che si presentano nella forma indeterminata.Si pensi che il marchese De l’Hospital visse nella metà del 1600 ed era allievo di Bernoulli; quest’ultimo fu un grande matematico svizzero esperto di calcolo differenziale e integrale: in tale famiglia sicuramente la matematica e la fisica eranon di casa. Il conosciuto teorema di Bernoulli, applicato nella dinamica dei fluidi e che giustifica il volo degli aerei, è stato elaborato dal figlio.
Ritengo fondamentale che la trattazione dell’analisi ponga l’argomento delle derivate dopo quello dei limiti e che quest’ultimi vengano spiegati tramite la teoria NSA; grazie a ciò l’applicazione del menzionato teorema ha la sua massima valenza.
Ecco il teorema:
Se sviluppando un limite ci si trova nella forma:
![]()
oppure nella forma:
![]()
allora si può applicare il teorema:
(1) ![]()
ossia posso fare la derivata del numeratore e del denominatore
N.B. NON LA DERIVATA DEL QUOZIENTE DI FUNZIONE ma la DERIVATA DEL NUMERATORE E DEL DENOMINATORE!
La (1) vale anche in questo caso:
(2) ![]()
Esempio nel caso ![]()
![]() =2
=2
Esempio nel caso ![]()
![]()
Una retta sul piano può essere parallela all’asse delle ascisse (orizzontale), parallela all’asse delle ordinate (verticale) e quindi, conseguentemente anche obliqua.
In maniera analoga un asintoto può essere verticale, orizzontale ed obliquo.
Per la presenza di un asintoto obliquo DEVONO essere vere le seguenti due condizioni basta che una delle due non sia soddisfatta che l’asintoto non sia presente:
(1) ![]()
che mi fornisce il coefficiente angolare della “retta” asintoto
(2) ![]()
Ribadisco il fatto che è sufficiente che una delle due non sia vera ossia che mi dia un limite non finito affinché non vi sia il limite obliquo.
Ecco immediatamente un esempio:
sia ![]()
allora applico la (1)
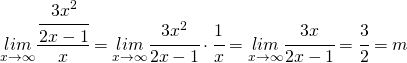
adesso applico la (2) per trovare la ![]()
![Rendered by QuickLaTeX.com \underset{x\rightarrow\infty}{lim}\left[\cfrac{3x^{2}}{2x-1}-\cfrac{3}{2}x\right]=\underset{x\rightarrow\infty}{lim}\cfrac{6x^{2}-3x(2x-1)}{(2x-1)\cdot2}=\underset{x\rightarrow\infty}{lim}\cfrac{6x^{2}-6x^{2}+3x}{(2x-1)\cdot2}=\underset{x\rightarrow\infty}{lim}\cfrac{3x}{4x-2}=\cfrac{3}{4}=q](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8c7607f686ead3f6506f65e7541a9133_l3.png)
l’asintoto è:
![]()
Il grafico risulta:
Un asintoto oltre che verticale può essere anche orizzontale, ossia parallelo all’asse delle ascisse.
Per la sua presenza deve valere la seguente relazione:
(1) ![]()
La (1) afferma che quando x assume valori molto grandi, infinitamente grandi, la funzione tende a un valore finito ossia ad un asintoto orizzontale.
Ecco alcuni esempi della presenza di asintoti verticali:
(2) ![]()
in questo caso la (2) ci fornisce un asintoto orizzontale con valore
![]()
Per meglio evidenziare tale fatto ecco il grafico della funzione:
(3) ![]()
in questo caso l’asintoto è:
![]()
Ecco il grafico della funzione:
Prima di cominciare gli esercizi, preferisco ridefinire il procedimento.
m.c.m. lettere comuni e non comuni con il massimo esponente.
M.C.D. SOLO lettere comuni con l’esponente più basso
Determinare il m.c.m ed il M.C.D. trai seguenti monomi:
1) ![]() ;
; ![]() ;
; ![]()
2) ![]() ;
; ![]() ;
; ![]()
3) ![]() ;
;![]() ;
; ![]()
4) ![]() ;
;![]() ;
; ![]()
5) ![]() ;
; ![]() ;
; ![]()
6) ![]() ;
; ![]() ;
; ![]()
7) ![]() ;
; ![]() ;
; ![]()
8) ![]() ;
; ![]() ;
; ![]()
Nell’introduzione avevo accennato al fatto che studiare cosa accade ad una funzione nell’intorno di un punto significa studiare il limite a destra e a sinistra.Tale studio, com’è consuetudine, in analisi si riassume in tali forme:
(1) ![]()
(2) ![]()
la (1) descrive il fatto che si studia l’andamento della funzione quando ci si avvicina al valore ![]() provenendo da destra.
provenendo da destra.
la (2) descrive il fatto che si studia l’andamento della funzione quando ci si avvicina al valore ![]() provenendo da sinistra.
provenendo da sinistra.
Ad esempio: assumo che ![]() allora provenire da sinistra significa prendere i seguenti valori: 1,8; 1,9; 1,91 e così via; provenire da destra significa prendere i seguenti valori 2,2; 2,1; 2,001 e così via.
allora provenire da sinistra significa prendere i seguenti valori: 1,8; 1,9; 1,91 e così via; provenire da destra significa prendere i seguenti valori 2,2; 2,1; 2,001 e così via.
Ancora provenire da destra significa prendere valori ![]() mentre provenire da sinistra significa prendere valori
mentre provenire da sinistra significa prendere valori ![]() .
.
Per capire se la funzione assume un valore ![]() o
o ![]() si deve studiare il segno della funzione in un intorno del valore a cui tende la
si deve studiare il segno della funzione in un intorno del valore a cui tende la ![]() .
.
Ecco un esempio:
(3) ![]()
(4) ![]()
Infatti:
– il dominio è tutto ![]() escludendo il valore in cui si annulla il denominatore ossia 2.
escludendo il valore in cui si annulla il denominatore ossia 2.
– devo studiare la seguente disequazione:
![]() .
.
Per ![]() la funzione è positiva mentre per
la funzione è positiva mentre per ![]() la funzione è negativa.
la funzione è negativa.
La regola è:
per studiare i limiti nella forma (1) e (2) si deve studiare la disequazione della funzione di cui si deve studiare il limite.
Tale regola giustifica il continuo studio delle disequazioni frazionarie negli anni scolastici precedenti!
Quindi si ha sempre un asintoto verticale ma la funzione ha un andamento diverso.
Il grafico della funzione:
![]() è:
è:
Si nota che:
all’avvicinarsi a 2 da destra la funzione assume valori sempre positivi al limite infinitesimamente positivi;
all’avvicinarsi a 2 da sinistra la funzione assume valori sempre negativi al limite infinitesimamente negativi.