Per affrontare con sicurezza questa parte dell’INVALSI è necessario avere queste competenze:
- raccoglimento tra potenze. Ad esempio:
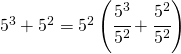
![]()
- proprietà tra potenze.
Ad esempio:
![]()
- aver capito bene il significato della numerazione a base 10.
Ad esempio

Per affrontare con sicurezza questa parte dell’INVALSI è necessario avere queste competenze:
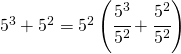
![]()
Ad esempio:
![]()
Ad esempio

Igor Morski
Quale metodo usare per risolvere i sistemi d’equazione nel minor tempo possibile e in maniera corretta?
Qui inserisco una serie di esercizi e nelle soluzioni inserisco il metodo che io ritengo migliore ma non necessariamente quello che tutti possono ritenere migliore. Alla fine uno può trovarsi meglio aver usato un metodo invece che un altro.
Esercizi facili per prendere la mano (6)
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
![Rendered by QuickLaTeX.com \left [ \left ( 1,\cfrac{3}{2} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-bc1069d7f684e3b18c1030db0db3c4be_l3.png) |
| 6.7. |
Esercizi più complessi (7)
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
7.4. 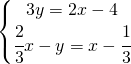 |
![Rendered by QuickLaTeX.com \left [ \left ( \cfrac{5}{3},-\cfrac{2}{9} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-97bb486ade1c64964c37a04a3fde6c30_l3.png) |
7.5. 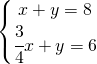 |
|
7.6. 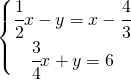 |
Verso un buon livello (8)
8.1. 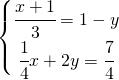 |
|
Verso il l’ottimo (9)
9.1. 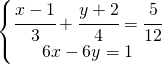 |
![Rendered by QuickLaTeX.com \left [ \left (\cfrac{1}{2},\cfrac{1}{3} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-801c5aa12d2b23cdf869d61901284917_l3.png) |
L’ottimo (10)
10.1. 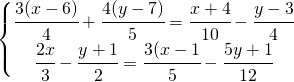 |
|
Si studi la seguente parabola:
![]()
primo passo: intersezioni con gli assi:
pongo x=0
allora si ha:
y=-4
pongo y=0
devo risolvere l’equazione
![]()
per esercitarsi su questo tipo di equazioni si può andare al seguente link:
risoluzione equazioni di secondo grado pure
che ha come soluzioni:
![]()
secondo passo: analisi della concavità
A=1
essendo positiva la concavità è sempre verso l’alto
terzo passo: calcolo del vertice
A=1; B=0; C=-4
![]()
![]()
Le parabole pure sono del tipo:
![]()
![]()
![]()
che più velocemente viene scritta come
![]()
Studio adesso quest’ultima.
Passo1: intersezioni con gli assi:
x=0
allora
y=0
ancora, se metto y=0
la x è ancora 0.
Passo 2: analisi della concavità
A=1
ossia la concavità è verso l’alto
Passo 3: coordinate del vertice
![]()
![]()
quindi li grafico risulta
Per parabola spuria considero di questo tipo:
![]()
1 passo: intersezioni con gli assi
pongo
![]()
ed ho:
![]()
pongo
![]()
![]()
questa volta non serve usare la formula risolutiva per l’equazione di secondo grado ma è sufficiente raccogliere la x ossia:
![]()
la prima parte conferma la soluzione già trovata precedentemente ossia
x=0
la seconda è la soluzione dell’equazione di primo grado:
![]()
ossia
![]()
passo2: analisi del coefficiente A per capire la concavità
A=1
per cui la concavità è verso l’alto.
Il grafico risulta quindi:
passo3: calcolo delle coordinate del vertice
A=1; B=-4; C=0
![]()
![]()
[:it] Rappresentare sul piano cartesiano la parabola di equazione
Rappresentare sul piano cartesiano la parabola di equazione
![]()
1 punto: intersezioni con gli assi
calcolo dell’intersezione.
Pongo la x=0 ed ho
y=20.
Adesso pongo la y=0 e devo risolvere l’equazione di secondo grado:
![]()
identifico la A, la B e la C ossia i tre coefficienti che mi permettono di risolvere l’equazione di secondo grado.
A= 1
B= -9
C=20
Li sostituisco nella:
![]()
e viene:
![]()
ho le seguenti intersezioni:
![]()
e
![]()
2 punto: analisi del segno di A
la A=1 quindi la parabola ha la concavità verso l’alto ossia è così fatta:
3 punto: coordinate del vertice
![]()
![]()
[:en] Rappresentare sul piano cartesiano la parabola di equazione
Rappresentare sul piano cartesiano la parabola di equazione
![]()
1 punto: intersezioni con gli assi
calcolo dell’intersezione.
Pongo la x=0 ed ho
y=20.
Adesso pongo la y=0 e devo risolvere l’equazione di secondo grado:
![]()
identifico la A, la B e la C ossia i tre coefficienti che mi permettono di risolvere l’equazione di secondo grado.
A= 1
B= -9
C=20
Li sostituisco nella:
![]()
e viene:
![]()
ho le seguenti intersezioni:
![]()
e
![]()
2 punto: analisi del segno di A
la A=1 quindi la parabola ha la concavità verso l’alto ossia è così fatta:
3 punto: coordinate del vertice
![]()
![]()
(versione tedesca)[:de]

Jim Warren
Stelle diejenige Parabel auf dem Koordinatensystem dar:
![]()
Punkt 1: Interasektion der Axen
Rechnung der Intersektionen
Stelle x=0 und man erhält
y=20.
Jetzt stelle ich y=0 und muss die Gleichung des zweiten Grades lösen
![]()
Ich identifiziere A,B und C als drei Koefitienten, die mir die Möglichkeit geben die Gleichung des zweiten Grades zu lösen.
A= 1
B= -9
C=20
Ích ersetze sie:
![]()
und man hat:
![]()
man hat die folgenden Intersektionen:
![]()
und
![]()
Punkt 2: Analyse des Zeichens A
Das A=1, also die Parabel hat Höhlung von unten nach oben; und wird so dargestellt:
Punkt 3: Koordinaten des Scheitelpunktes der Parabel:
![]()
![]() [:]
[:]
 I passi per rappresentare un parabola sul piano cartesiano sono
I passi per rappresentare un parabola sul piano cartesiano sono
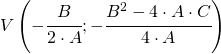
 Tale raccolta nasce per creare un modulo di approfondimento per affrontare quella pletora di argomenti sul piano cartesiano e retta.
Tale raccolta nasce per creare un modulo di approfondimento per affrontare quella pletora di argomenti sul piano cartesiano e retta.