
Jacek Yerka
[WpProQuiz 14]


Jacek Yerka
[WpProQuiz 14]
 [WpProQuiz 13]
[WpProQuiz 13]
 [WpProQuiz 12]
[WpProQuiz 12]

Giuseppe Muscio
[WpProQuiz 11]
 La definizione formale di dominio di una funzione è:
La definizione formale di dominio di una funzione è:
insieme dei valori possibili che la variabile indipendente x può assumere, in modo che la funzione sia definita in tali valori.
In molti anni che insegno ho adottato questa definizione:
insieme dei valori di x per i quali posso DISEGNARE la funzione.
Questa definizione, indubbiamente molto spartana, mi ha consentito di poter far capire perché dal dominio devono essere esclusi quei punti in cui la funzione presenta un asintoto.
Infatti se si pensa, l’infinito non si può disegnare e quando una funzione tende all’infinito per un particolare punto, non può essere disegnata per cui tale punto deve essere escluso dal dominio stesso!
Ecco i domini delle funzioni più comuni:
Funzione polinomiale
La retta è una funzione polinomiale y=3x+5 il cui grafico è:
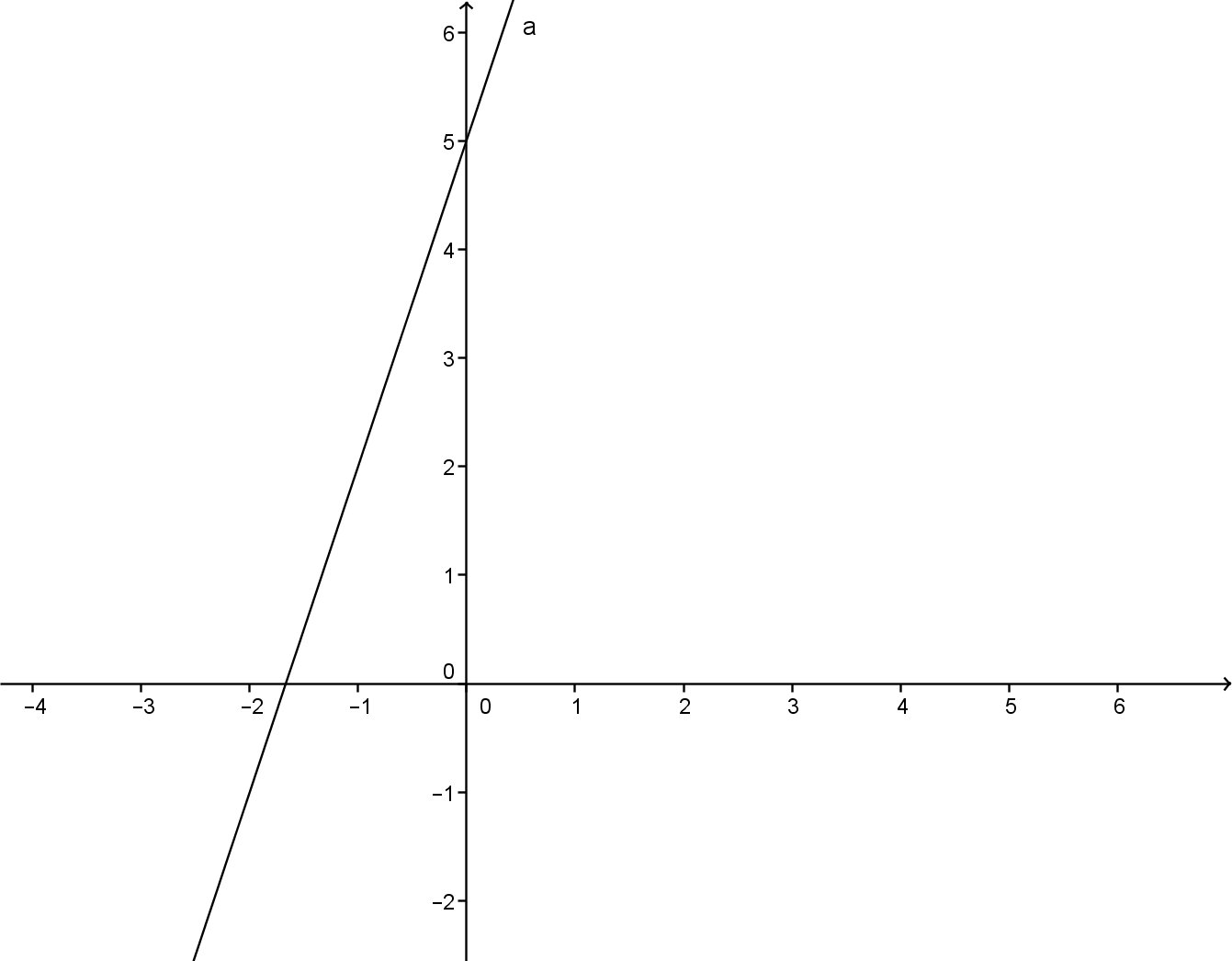
si nota dal grafico che il disegno esiste per ogni valore di x e si scrive:
![]()
La parabola è una funzione polinomiale:
![]()
il cui grafico è:
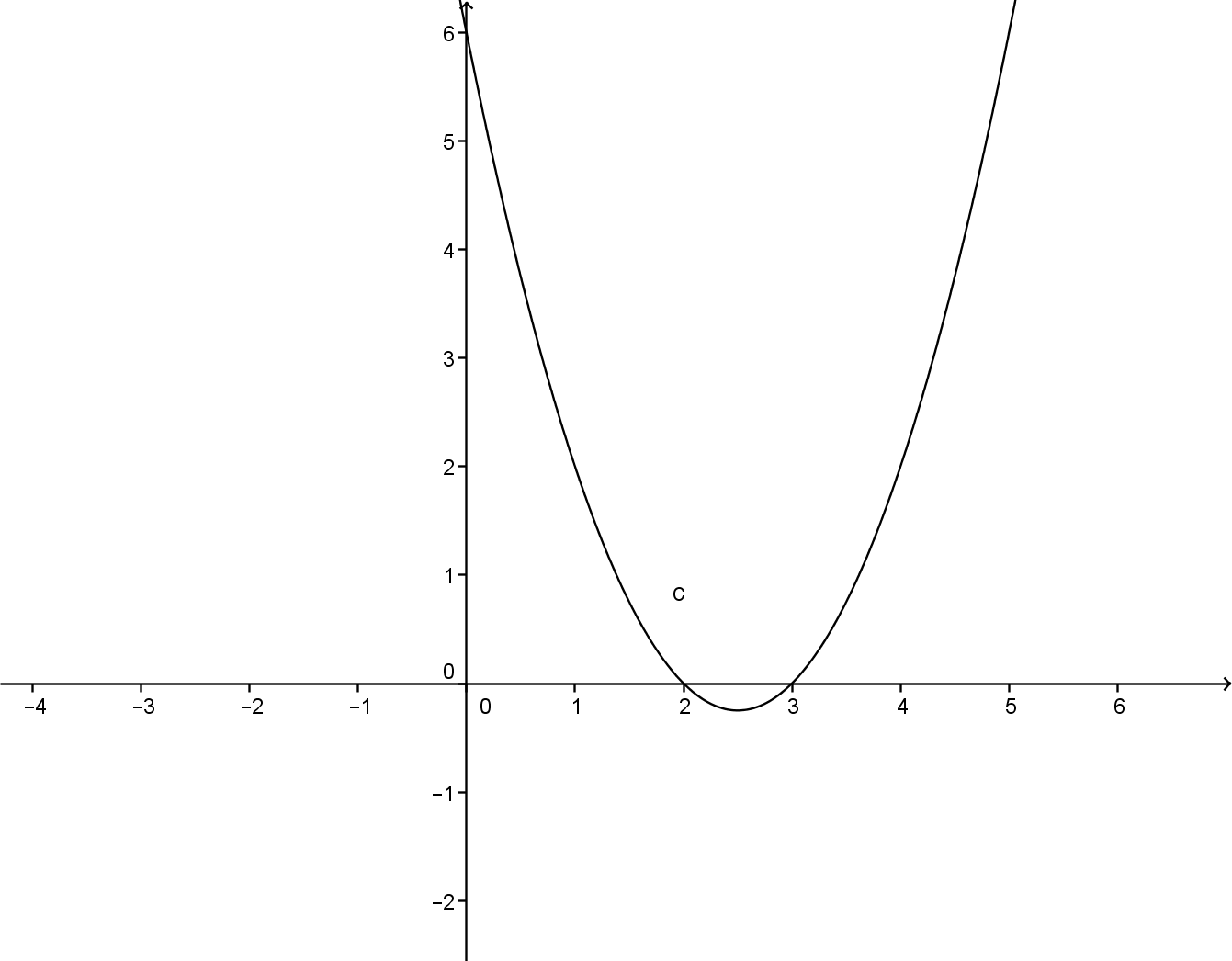 ed il dominio è:
ed il dominio è:
![]()
Generalizzando
tutte le funzioni del tipo:
![]()
hanno dominio:
![]()
Funzione frazionaria
Ecco il grafico di una funzione frazionaria: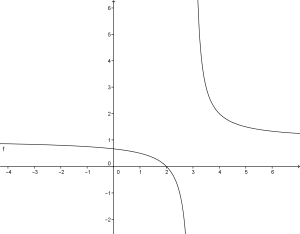 si noti subito che nell’intorno del numero 3 la funzione si avvicina sempre più al 3 (asintoto verticale) senza mai toccarlo.
si noti subito che nell’intorno del numero 3 la funzione si avvicina sempre più al 3 (asintoto verticale) senza mai toccarlo.
La funzione frazionaria ha al numeratore un polinomio ed al denominatore un altro polinomio.
Il grafico precedente ha equazione:
![]()
e per determinare il dominio devo escludere i valori che annullano il denominatore ossia risolvere questa diseguaglianza:
![]()
ossia
![]()
il dominio diventa:
![]()
generalizzando:
Si devono trovare i valori che annullano il denominatore.
Se
![]()
i valori che annullano il denominatore sono:
![]()
il dominio diventa quindi:
![]()
Funzione irrazionale
Ecco la rappresentazione sul piano cartesiano di una funzione irrazionale:
 essa ha come equazione:
essa ha come equazione:
![]()
per studiare il dominio bisogna porre l’argomento della radice quadrata sempre strettamente maggiore di zero.
Ossia
![]()
Il dominio diventa:
![]()
generalizzando; data la funzione:
![]()
con n pari, bisogna studiare il segno dell’argomento ossia porre:
![]()
il dominio diventa quindi:
![]()
Funzione esponenziale
Ecco la rappresentazione grafica di una funzione esponenziale:
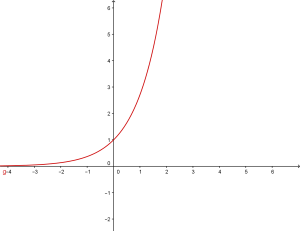 la cui equazione è:
la cui equazione è:
![]()
il cui dominio coincide con le funzioni polinomiali ossia:
![]()
generalizzando:
![]() con
con
A(x) una funzione polinomiale
Si ha quindi sempre come dominio:
![]()
Funzione logaritmica
Ecco il grafico:
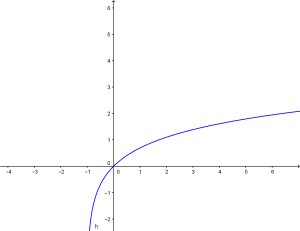 che ha equazione:
che ha equazione:
![]()
e per determinare il suo dominio devo prendere l’argomento e porlo maggiore di 0:
![]()
Quindi il dominio si scrive:
![]()
generalizzando:
![]()
bisogna porre sempre l’argomento maggiore di zero (non anche uguale a zero perché in 0 il logaritmo ha un asintoto verticale).
![]()
Combinazione delle funzioni precedenti
Per studiare il dominio dato dalla combinazione di una delle precedenti funzioni bisogna impostare un sistema di disequazioni o diseguaglianze e come soluzione si ha quell’insieme di valori che vanno bene a tutti.
 Questo problema è stato tratto da La settimana Enigmistica del 24 dicembre 2015 quesito 7063 e dato alla verifica sui sistemi d’equazione alle classi di seconda superiore il 13 gennaio 2016.
Questo problema è stato tratto da La settimana Enigmistica del 24 dicembre 2015 quesito 7063 e dato alla verifica sui sistemi d’equazione alle classi di seconda superiore il 13 gennaio 2016.
“Biagio, Fulvio e Giacomo sono tre studenti universitari di matematica. Per raggranellare qualche soldo, nel mese di dicembre, si sono ritrovati a lavorare in un grande magazzino, nel reparto degli addobbi natalizi. Forti della loro padronanza dei numeri, a volte si divertivano a mettere qualcuno in difficoltà. Così, a un signore troppo pignolo,
Ma quando il cliente, frastornato, è giunto alla cassa, si è scoperto che uno di loro aveva mentito mentre gli altri due avevano dato informazioni corrette.
Chi ha dato informazioni errate?
Soluzione:
Si imposta un sistema di equazione con
p palline
a angioletti
s stelle
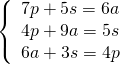
Adesso li ordino ed ho:
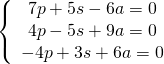
Suppongo che le prime due ossia Biagio e Fulvio abbiano detto la verità e le sommo:
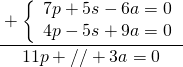
che risolta dà:
![]()
che è impossibile in quanto le palline non possono dare un costo negativo.
Per cui o Biagio o Fulvio ha detto il falso!
Adesso sommo Fulvio e Giacomo
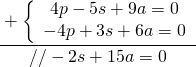
ossia
![]()
che è possibile.
Per cui chi dice il falso è Biagio.

Sergey Tyukanov
[WpProQuiz 8]
 [WpProQuiz 7]
[WpProQuiz 7]
 [WpProQuiz 6]
[WpProQuiz 6]

Esempi sulle precedenti proprietà