Tutti i seguenti quiz possono essere affrontati dopo aver compreso come effettuare le derivate, conoscere le disequazioni e le equazioni di primo e secondo grado.
Tutti i seguenti quiz possono essere affrontati dopo aver compreso come effettuare le derivate, conoscere le disequazioni e le equazioni di primo e secondo grado.
[WpProQuiz 17]
[WpProQuiz 18]
[WpProQuiz 19]
[WpProQuiz 20]
[WpProQuiz 21]

 Tutti i seguenti quiz possono essere affrontati dopo aver compreso come effettuare le derivate, conoscere le disequazioni e le equazioni di primo e secondo grado.
Tutti i seguenti quiz possono essere affrontati dopo aver compreso come effettuare le derivate, conoscere le disequazioni e le equazioni di primo e secondo grado.
[WpProQuiz 17]
[WpProQuiz 18]
[WpProQuiz 19]
[WpProQuiz 20]
[WpProQuiz 21]
 La probabilità di un evento è la misura del grado di fiducia che una persona ha nel verificarsi dell’evento.
La probabilità di un evento è la misura del grado di fiducia che una persona ha nel verificarsi dell’evento.
La definizione formale è la seguente:
la probabilità di un evento aleatorio, previsto da una determinata prova, è data dal rapporto tra il numero dei casi favorevoli all’evento (cioè il numero dei modi diversi di realizzarsi dell’evento) e il numero dei casi possibili, nell’ipotesi c he i casi siano tutti egualmente possibili.
Algebricamente si ha:
![]()
dove ![]() è il numero di casi favorevoli ed
è il numero di casi favorevoli ed ![]() è il numero dei casi possibili.
è il numero dei casi possibili.
Esempio per capire immediatamente la definizione.
Es1.
si calcoli la probabilità che lanciando un dado esca:
Svolgimento:
Per prima cosa si debba considerare lo spazio degli eventi:
![]()
i cui eventi sono i sei casi possibili possibili.
I casi favorevoli sono:
a. uno in quanto l’evento si realizza in un solo modo (uscita del numero 6), per cui la probabilità è
![]()
b. tre in quanto l’evento si realizza in tre modi diversi (uscita dell’1, uscita del 3, uscita del 5), per cui la probabilità è:
![]()
c. sei, in quanto tutti i risultati sono favorevoli, per cui la probabilità vale:
![]()
d. zero, per cui la probilità è nulla e l’evento è impossibile.
 Data la seguente equazione frazionaria:
Data la seguente equazione frazionaria:
![]()
allora moltiplico prima a sinistra e a destra per ![]()
e si ha:
![]()
![]()
moltiplico a sinistra e a destra per ![]()
![]()
![]()
sviluppo la moltiplicazione
![]()
![]()
![]()
non avendo studiato l campo d’accettabilità devo valutare se la soluzione è accettabile o meno; questo significa che se mi dovessi trovare nella situazione ![]() ossia con un denominatore nullo a prescindere dal valore numerico la soluzione NON è accettabile.
ossia con un denominatore nullo a prescindere dal valore numerico la soluzione NON è accettabile.
Sostituisco nell’equazione di partenza il 5 e si ha:
![]()
![]()
![]()
ed essendo un’identità e non ricadendo nel caso di soluzione non accettabile effettivamente ![]() è la soluzione.
è la soluzione.
 Il metodo di Cramer lo applico al seguente sistema:
Il metodo di Cramer lo applico al seguente sistema:
![]()
Si notino le seguenti cose:
Per trovare il valore della x:
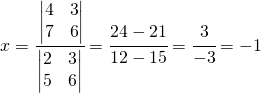
Per trovare il valore della y:
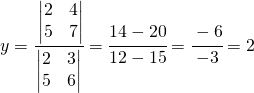
Spiegazione:
 Questo metodo presuppone la conoscenza di una nuova operazione che si chiama determinante.
Questo metodo presuppone la conoscenza di una nuova operazione che si chiama determinante.
Il determinante è un’operazione che si applica ad una nuova struttura con cui si possono guardare i numeri di un sistema d’equazione che si chiama matrice.
Una matrice è una combinazione opportuna di righe e di colonne. In questo momento considero solo la matrice con due righe e due colonne ad esempio:
![]()
e l’operazione determinante è un opportuno prodotto e differenza tra i numeri che compongono la matrice
In generale data la seguente matrice:
![]()
il determinante, e si scrive così (si noti che si sono sostituite le due parentesi quadre con due barre verticali), risulta:
![]()
Nell’esempio precedente:
![]()
 6.1.1. Data la seguente equazione
6.1.1. Data la seguente equazione ![]() posso identificare
posso identificare ![]() ,
, ![]() e
e ![]() .
.
![]()
![]()
quindi il centro ha equazione:
![]()
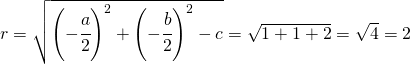
A questo punto per rappresentare la circonferenza sul piano cartesiano fisso prima il centro e poi posso usare il raggio.
Posso inoltre determinare le intersezioni con gli assi impostando i seguenti due sistemi:
Per le intersezioni con l’asse delle y
![]()
Per le intersezioni con l’asse delle x
![]()
il primo sistema comporta il risolvere l’equazione:
![]()
(equazioni di secondo grado) le cui soluzioni sono:
![]()
il secondo sistema comporta il risolvere l’equazione:
![]()
le cui soluzioni sono:
![]()
Il grafico risulta quindi:
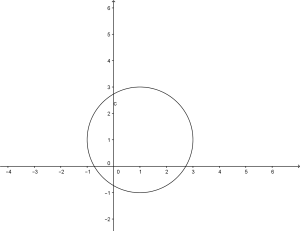
6.2.1. Dati ![]() trovare l’equazione della circonferenza.
trovare l’equazione della circonferenza.
Si parte questa volta da questa forma della circonferenza:
![]()
in cui ![]() e
e ![]() sono le coordinate del centro ed
sono le coordinate del centro ed ![]() è il valore del raggio.
è il valore del raggio.
Sostituendo quindi i dati del problema si ha:
![]()
sviluppando i prodotti notevoli ho:
![]()
riordino l’equazione:
![]()
![]()
che è la richiesta del problema
7.3.
Dato il centro ed un punto ![]() per determinare l’equazione della circonferenza calcolo la distanza tra il centro C ed il punto P che rappresenta il raggio.
per determinare l’equazione della circonferenza calcolo la distanza tra il centro C ed il punto P che rappresenta il raggio.
![]()
Adesso utilizzo la formula dato il centro ed il raggio che applicata diventa:
![]()
sviluppo le parentesi:
![]()
![]()
8.1. Equazione della circonferenza di diametro A e B.
![]()
il punto medio è il centro della circonferenza e quindi risulta:
![]()
![]()
quindi il centro risulta:
![]()
Adesso calcolo la distanza tra A e B ed il risultato lo divido per 2 e trovo il raggio.
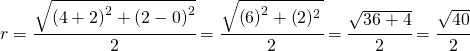
Adesso uso la formula che permette di ricavare l’equazione della circonferenza dato il centro ed il raggio.
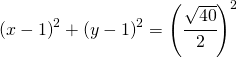
sviluppo le parentesi ed ho:
![]()
ordino i termini e sommo quelli simili:
![]()
9.1. Dati i seguenti tre punti calcolare l’equazione della circonferenza.
![]()
Si deve partire dal fatto che per verificare che un punto appartenga ad una funzione deve valere l’identità ossia se sostituisco le coordinate di un punto nell’equazione generica della circonferenza ![]() devo trovare un’identità.
devo trovare un’identità.
Sostituisco le coordinate di A:
![]()
![]()
Sostituisco le coordinate di B:
![]()
![]()
Sostituisco le coordinate di C:
![]()
![]()
![]()
Ho tre equazioni in tre incognite e devo saper risolvere un sistema a tre equazioni in tre incognite.
Se si dovesse avere difficoltà nel risolvere il sistema d’equazioni andare a rivedersi il post:
sistemi d’equazione metodo della sostituzione
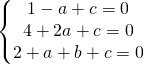
utilizzo appunto il metodo della sostituzione andando a sostituire il valore di c nella seconda e nella terza equazione.
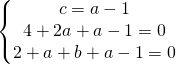
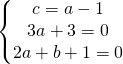
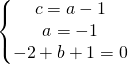
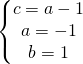
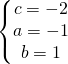
Adesso sostituisco i valori trovati nell’equazione generica della circonferenza:
![]()
che è il risultato voluto.
 Gli esercizi sulla circonferenza sono normalmente di questo tipo:
Gli esercizi sulla circonferenza sono normalmente di questo tipo:
Esercizi elementari (6) di tipo 1: determinazione centro e raggio e relativo disegno
| 6.1.1. |
|
| 6.1.2 |
|
| 6.1.3. |
|
| 6.1.4. |
|
| 6.1.5. |
Esercizi elementari (6) di tipo 2: determinazione dell’equazione della circonferenza dato il centro ed il raggio
| 6.2.1. |
|
| 6.2.2. |
Esercizi per un livello discreto (7): determinazione centro e raggio e rappresentazione sul piano cartesiano
| 7.1. |
![Rendered by QuickLaTeX.com \left [ C\left ( 1;\cfrac{1}{2} \right );r=\cfrac{\sqrt{3}}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2241daf9b8fb29c1389d640b1a9095f2_l3.png) |
| 7.2. |
![Rendered by QuickLaTeX.com \left [ C\left ( \cfrac{1}{2};1 \right );r=2 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2d6b347a7a547e6cbe792851e0df679e_l3.png) |
Determinare l’equazione della circonferenza che ha centro in C e passa per P, e rappresentala graficamente.
Per sviluppare tali esercizi è necessario conoscere la distanza tra due punti
| 7.3. |
|
| 7.4. |
|
| 7.5 |
|
| 7.6. |
|
| 7.7. |
Per essere in grado di sviluppare questi esercizi è necessario conoscere come calcolare il punto medio di un segmento.
Esercizi per un buon livello (8): scrivi l’equazione delle circonferenze di diametro AB e rappresentale sul piano
| 8.1. |
|
| 8.2. |
|
| 8.3. |
|
| 8.4. |
|
| 8.5. |
Esercizi per un livello che dimostra una certa sicurezza nell’operare (9-10).
Quello che serve conoscere è la condizione di appartenenza di un punto ad una funzione e sape risolvere un sistema di tre equazioni in tre incognite.
Scrivi l’equazione della circonferenza passante per i punti A, B, C e rappresentala graficamente.
| 9.1. |
|
| 9.2. |
|
| 9.3. |
|
| 9.4. |
|
| 9.5. |
|
| 9.6. |
|
Questi esercizi sono utili per verificare la capacità di saper risolvere un sistema d’equazione.
Per avere un’ottima manualità (10)
Determinare la posizione reciproca della retta e della circonferenza e determinare gli eventuali punti d’intersezione
| 10.1 |
|
| 10.2. |
|
| 10.3. |
|
| 10.4. |
|
| 10.5. |
|
| 10.6. |
Problemi che mettono in evidenza le competenze:
C1. Scrivi l’equazione della circonferenza che ha centro in (-1;3) ed è tangente all’asse y.
![]()
C2. Determina l’equazione della circonferenza ce ha centro nell’origine ed è tangente alla retta di equazione ![]()
![]()
C3. Scrivi l’equazione della circonferenza avente il centro di ordinata uguale a 3 e passante per i punti A(8;9) e B(12;1).
![]()
[:it]

Jacek Yerka
La circonferenza è quel luogo del piano descritto da tutti quei punti equidistanti da un punto C chiamato centro.
Si forniscono normalmente queste due equazioni che sono equivalenti ma applicabili in ambiti diversi a seconda dei dati che si forniscono o di cosa si deve trovare.
Prima forma
![]()
in questo caso le coordinate del centro in funzione di a e b sono:
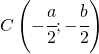
ed il raggio è:
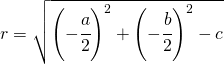
Seconda forma
![]()
le cui coordinate del centro sono:
![]()
ed il raggio è appunto
![]()
[:en]

Jacek Yerka
La circonferenza è quel luogo del piano descritto da tutti quei punti equidistanti da un punto C chiamato centro.
Si forniscono normalmente queste due equazioni che sono equivalenti ma applicabili in ambiti diversi a seconda dei dati che si forniscono o di cosa si deve trovare.
Prima forma
![]()
in questo caso le coordinate del centro in funzione di a e b sono:
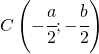
ed il raggio è:
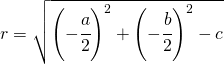
Seconda forma
![]()
le cui coordinate del centro sono:
![]()
ed il raggio è appunto
![]()
[:de]

Jacek Jerka
Der Umfang ist der Ort der Ebene, der von all diesen Punkten von einem Punkt gleich weit entfernt ist und C genannt wird.
In der Regel werden diese beiden Gleichungen geliefert, die gleichwertig sind, aber in verschiedenen Bereichen in Abhängigkeit der angegebenen Daten anwendbar sind oder von dem, was gesucht wird, abhängig sind.
Erste Form
![]()
In diesem Fall sind die Koordinaten der Mitte in Funktion von a und b folgende :
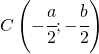
und der Radius ist :
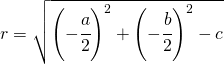
Zweite Form
![]()
Die Koordinaten der Mitte sind:
![]()
und der Radius ist demzufolge
![]() [:]
[:]
 Le disequazioni di secondo grado possono essere risolte o applicando la scomposizione del polinomio di secondo grado o attraverso il metodo grafico o della parabola.
Le disequazioni di secondo grado possono essere risolte o applicando la scomposizione del polinomio di secondo grado o attraverso il metodo grafico o della parabola.
Scomposizione del polinomio di secondo grado
un polinomio di secondo grado può sempre essere scritto come:
![]()
dove
![]()
sono le soluzioni dell’equazione
![]()
quindi si studia il grafico per determinare il segno finale della disequazione:
![]()
o della disequazione:
![]()
Unica avvertenza studiare SEMPRE
![]()
e
![]()
ed il segno di a
Con questi esempi spero di chiarire la cosa:
Es1.
![]()
risolvo l’equazione:
![]()
essa ha soluzione:
![]()
e la
a=1
Studio il segno di
![]()
![]()
Rappresento graficamente la soluzione evidenziando che essendo un prodotto verifico dove il prodotto fornisce il segno positivo.
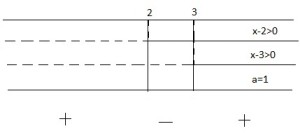 Si noti che la a=1 e quindi la si rappresenta con una linea continua.
Si noti che la a=1 e quindi la si rappresenta con una linea continua.
La soluzione è
![]()
Es2.
![]()
risolvo l’equazione:
![]()
essa ha soluzione:
![]()
e la
a=1
Studio il segno di
![]()
![]()
Si NOTA che si studia comunque il segno maggiore di zero!
Rappresento graficamente la soluzione evidenziando che essendo un prodotto verifico dove il prodotto fornisce il segno Negativo questa volta

La soluzione, questa volta è:
![]()
Es3.
![]()
risolvo l’equazione:
![]()
essa ha soluzione:
![]()
e la
a=-1
Studio il segno di
![]()
![]()
Rappresento graficamente la soluzione evidenziando che essendo un prodotto verifico dove il prodotto fornisce il segno positivo
Si noti che questa volta la a=-1 ossia viene rappresentata con una linea tratteggiata.
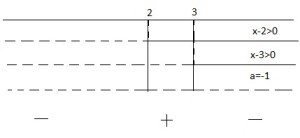 devo studiare dove si ha il segno positivo ed è tra 2 e 3.
devo studiare dove si ha il segno positivo ed è tra 2 e 3.
![]()
Metodo grafico
Il metodo grafico è molto semplice, è sufficiente conoscere la rappresentazione di una parabola e le sue intersezioni con l’asse delle x che sono le soluzioni della relativa equazione di secondo grado.
Es1.
![]()
risolvo l’equazione:
![]()
essa ha soluzione:
![]()
e la
a=1
la rappresentazione sul piano cartesiano è:
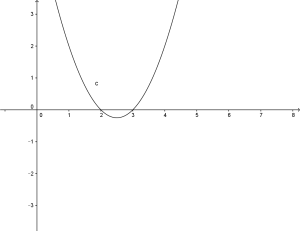
Si noti subito che la parabola è sopra l’asse delle x per quei valori per cui:
![]() .
.
Es2.
Nel secondo esempio si deve studiare:
![]()
Il procedimento è uguale all’esempio precedente ed il grafico pure:
 ma questa volta si vuole saper dov’è minore di zero:
ma questa volta si vuole saper dov’è minore di zero:
![]() .
.
Es3.
![]()
in questo caso le soluzioni sono sempre le stesse ma il grafico è:
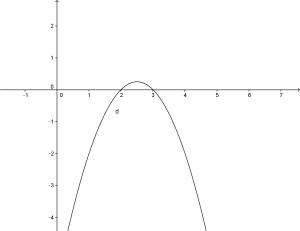 e dov’è maggiore di zero?
e dov’è maggiore di zero?
![]()
6.1.

![]()
Raccolgo le x a sinistra del verso della disequazione e i numeri a destra.
Per fare questo sommo a sinistra e destra
![]() .
.
![]() .
.
![]() .
.
![]()
Vale sempre il fatto che il numero che moltiplica la x debba essere l’1 per cui divido a destra e a sinistra per 2
![]()
la soluzione è:
![]()
Bisogna sempre fare la rappresentazione grafica della soluzione:
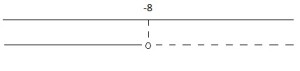 6.2.
6.2.
![]() .
.
![]() .
.
![]() .
.
Siccome il coefficiente della x è negativo cambio di segno moltiplicando per -1 a sinistra e a destra e cambio il verso della disequazione.
![]() .
.
![]() .
.
![]()
7.1.
Primo metodo
![]()
in questo semplice caso si potrebbe direttamente raggruppare le x a sinistra del verso e i numeri a destra:
![]()
![]()
cambio il verso della disequazione:
![]()
quindi divido a sinistra e a destra per 3 ed ho:
![]()
![]()
![]()
Secondo metodo
![]()
Faccio il minimo comune multiplo a sinistra e a destra:
![]()
moltiplico per 2 a sinistra e a destra:
![]()
![]()
![]()
![]()
moltiplico per -1 a sinistra e a destra cambiando il verso della disequazione
![]()
![]()
![]()
e quindi
![]()
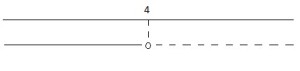
Graficamente è:
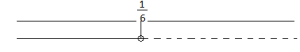 7.2.
7.2.
![]()
minimo comune multiplo
![]()
![]()
![]()
![]()
![]()
![]()
la soluzione è:
![]()
Graficamente
 8.1.
8.1.
![]()
Per essere in grado di affrontare agevolmente questa è necessario ricordarsi bene i prodotti notevoli.
La prima parentesi è il quadrato della differenza di un binomio, mentre l’ultima parentesi e la differenza del quadrato di un binomio.
![]()
Si noti come l’ultima parentesi l’ho tenuta in quanto vi è il simbolo – che modifica il segno di tutti i monomi presenti all’interno della parentesi.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
e la soluzione diventa:
![]()
Graficamente si ha: