
Renè Magritte

[:it]

Joel Rea
L’ellisse è quel luogo dei punti del piano per cui è costante la somma delle distanze da due punti fissi detti fuochi.
L’ellisse rappresenta ad esempio il percorso dei pianeti attorno al Sole, la forma stessa della Terra è ellittica, un uovo è ellittico, lo stesso cerchione di un pneumatico se non perfettamente rotondo viene rappresentato da un’ellisse.
Come nelle precedenti forme geometriche anche l’ellisse ha un’equazione che la rappresenta.
![]()
Se due fuochi dell’ellisse hanno coordinate:
![]()
allora ![]()
![]()
e l’ellisse ha questa rappresentazione grafica
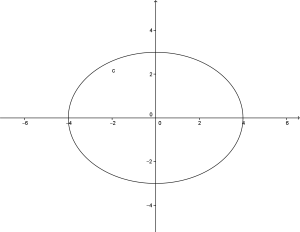
Se invece i due fuochi delle ellisse hanno coordinate:
![]()
allora ![]()
![]()
e l’ellisse ha questa rappresentazione grafica:
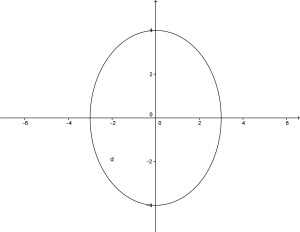 ma la
ma la ![]() e la
e la ![]() cosa rappresentano?
cosa rappresentano?
Danno la lunghezza dei semiassi dell’ellisse.
In pratica l’ellisse è racchiusa in un rettangolo i cui lati sono ![]() e
e ![]() .
.
Ossia si ha una figura del genere:
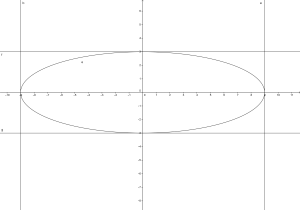 ma cosa differisce un’ellisse da una circonferenza?
ma cosa differisce un’ellisse da una circonferenza?
Dall’eccentricità ossia di quanto essa è schiacciata rispetto o l’asse x o l’asse y.
in pratica l’eccentricità è un rapporto tra la coordinata dei fuochi e l’asse maggiore dell’ellisse.
![]()
Nel caso della circonferenza ![]() per cui
per cui ![]() ed, infatti, l’eccentricità è nulla.[:en]
ed, infatti, l’eccentricità è nulla.[:en]

Joel Rea
L’ellisse è quel luogo dei punti del piano per cui è costante la somma delle distanze da due punti fissi detti fuochi.
L’ellisse rappresenta ad esempio il percorso dei pianeti attorno al Sole, la forma stessa della Terra è ellittica, un uovo è ellittico, lo stesso cerchione di un pneumatico se non perfettamente rotondo viene rappresentato da un’ellisse.
Come nelle precedenti forme geometriche anche l’ellisse ha un’equazione che la rappresenta.
![]()
Se due fuochi dell’ellisse hanno coordinate:
![]()
allora ![]() e l’ellisse ha questa rappresentazione grafica
e l’ellisse ha questa rappresentazione grafica

Se invece i due fuochi delle ellisse hanno coordinate:
![]()
allora ![]()
e l’ellisse ha questa rappresentazione grafica:
 ma la
ma la ![]() e la
e la ![]() cosa rappresentano?
cosa rappresentano?
Danno la lunghezza dei semiassi dell’ellisse.
In pratica l’ellisse è racchiusa in un rettangolo i cui lati sono ![]() e
e ![]() .
.
Ossia si ha una figura del genere:
 ma cosa differisce un’ellisse da una circonferenza?
ma cosa differisce un’ellisse da una circonferenza?
Dall’eccentricità ossi di quanto essa è schiacciata rispetto o l’asse x o l’asse y.
in pratica l’eccentricità è un rapporto tra la coordinata dei fuochi e l’asse maggiore dell’ellisse.
![]()
Nel caso della circonferenza ![]() per cui
per cui ![]() ed, infatti, l’eccentricità è nulla.[:de]
ed, infatti, l’eccentricità è nulla.[:de]
Die Ellipse
Eine Ellipse kann definiert werden als die Menge aller Punkte der Ebene, für die die Summe der Abstände zu zwei gegebenen Punkten und gleich einer gegebenen Konstante ist. Die Punkte und heißen Brennpunkte.
Die Ellipse repräsentiert zum Beispiel den Kurs von den Planeten um die Sonne, die gleiche Form von der Erde ist elliptisch, ein Ei ist elliptisch, Felgen von einem Reifen, wenn es nicht genau rund ist spricht man von einer Ellipse.
Wie auch die vorhergehenden geometrischen Formen wird die Ellipse durch eine Gleichung dargestellt.
Wenn zwei Brennpunkte der Ellipse Koordinaten haben,
hat die Ellipse diese grafische Darstellung
Wenn die Brennpunkte hingegen folgende Koordinaten haben,
hat die Ellipse diese grafische Darstellung
aber was stellen a und b dar?
Sie geben die Länge der Halbachsen der Ellipse an.
In der Praxis ist die Ellipse in einem Rechteck enthalten, dessen Seiten 2a und 2b sind.
Oder wir haben eine Form dieser Art:
Aber was unterscheidet eine Ellipse von einem Umfang?
Entweder die Exzentrizität oder wieviel die Ellipse hinsichtlich der Achse x oder y zerquetscht ist.
Die Exzentrizität ist also eine Beziehung zwischen der Koordinate der Brennpunkte und der größten Achse der Ellipse.
Wenn der Umfang a=b bzw. C=0, ist die Exzentrizität null.
[:]
[:it]

Rafal Olbinski
I dati sono ottenuti dalla seguente tabella:
| Stipendio mensile | N° di lavoratori |
| 1.300 | 2 |
| 1.700 | 22 |
| 2.200 | 19 |
| 2.600 | 3 |
| 6.500 | 2 |
| 9.400 | 1 |
| 23.000 | 1 |
La media aritmetica è di 2.700€
la mediana è di 2.200€
la moda è di 1.700€
Chi dei tre ha ragione?[:en]

Rafel Olbinski
I dati sono ottenuti dalla seguente tabella:
| Stipendio mensile | N° di lavoratori |
| 1.300 | 2 |
| 1.700 | 22 |
| 2.200 | 19 |
| 2.600 | 3 |
| 6.500 | 2 |
| 9.400 | 1 |
| 23.000 | 1 |
La media aritmetica è di 2.700€
la mediana è di 2.200€
la moda è di 1.700€
Chi dei tre ha ragione?[:de]

Rafel Olbinski
I dati sono ottenuti dalla seguente tabella:
| Stipendio mensile | N° di lavoratori |
| 1.300 | 2 |
| 1.700 | 22 |
| 2.200 | 19 |
| 2.600 | 3 |
| 6.500 | 2 |
| 9.400 | 1 |
| 23.000 | 1 |
La media aritmetica è di 2.700€
la mediana è di 2.200€
la moda è di 1.700€
Chi dei tre ha ragione?[:]
[:it]

Rafal Olbinski
La mediana (Me) è quel dato che divide l’insieme dei dati in due parti uguali.
L’idea che è alla base della mediana è quella di cercare un numero che sia più grande di un 50% delle osservazioni e più piccolo del restante 50%.
Spero con un esempio di chiarire il concetto:
Dati i seguenti valori:
71, 81, 90, 92, 94, 96, 97
Per trovare la mediana devo contare i valori che sono 7:
Il valore che sta esattamente nel mezzo è il 92 infatti esso ha alla sua sinistra 3 valori ed alla sua destra altri 3.
Quindi si deve pensare più che al valore di per sé alla sua posizione.
Per determinare quale valore prendere si prende quel valore che si trova alla posizione:
![]()
con n il numero dei valori.
Relazione che vale se il numero di valori è dispari
nel caso dell’esempio il calcolo precedente risulta:
![]()
ossia devo prendere il valore che si trova alla posizione 4 che è appunto il 92.
Inserisco questa tabella per chiarire maggiormente il concetto:
| valore | 71 | 81 | 90 | 92 | 94 | 96 | 97 |
| posizione | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Nel caso in cui invece il numero di valori è pari quale valore prendere?
Si prendono i due valori che stanno nella posizione ![]() e
e ![]() e si fa la loro media.
e si fa la loro media.
Un esempio spero che chiarisca il concetto.
Dati i valori
| Valore | 7 | 10 | 12 | 15 |
| Posizione | 1 | 2 | 3 | 4 |
n=4 che è pari per cui ho:
![]() che corrisponde al valore 10.
che corrisponde al valore 10.
![]() che corrisponde al valore 12.
che corrisponde al valore 12.
Adesso trovo la media tra questi due valori che è:
![]()
La moda è il valore che si presenta con maggiore frequenza.
Ad esempio dati i seguenti valori:
5,6,7,7,8.
La moda risulta 7 in quanto è il valore che si presenta con maggior frequenza.[:en]

Rafel Olbinski
La mediana (Me) è quel dato che divide l’insieme dei dati in due parti uguali.
L’idea che è alla base della mediana è quella di cercare un numero che sia più grande di un 50% delle osservazioni e più piccolo del restante 50%.
Spero con un esempio di chiarire il concetto:
Dati i seguenti valori:
71, 81, 90, 92, 94, 96, 97
Per trovare la mediana devo contare i valori che sono 7:
Il valore che sta esattamente nel mezzo è il 92 infatti esso ha alla sua sinistra 3 valori ed alla sua destra altri 3.
Quindi si deve pensare più che al valore di per sé alla sua posizione.
Per determinare quale valore prendere si prende quel valore che si trova alla posizione:
![]()
con n il numero dei valori.
Relazione che vale se il numero di valori è dispari
nel caso dell’esempio il calcolo precedente risulta:
![]()
ossia devo prendere il calore che si trova alla posizione 4 che è appunto il 92.
Inserisco questa tabella per chiarire maggiormente il concetto:
| valore | 71 | 81 | 90 | 92 | 94 | 96 | 97 |
| posizione | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Nel caso in cui invece il numero di valori è pari quale valore prendere?
Si prendono i due valori che stanno nella posizione ![]() e
e ![]() e si fa la loro media.
e si fa la loro media.
Un esempio spero che chiarisca il concetto.
Dati i valori
| Valore | 7 | 10 | 12 | 15 |
| Posizione | 1 | 2 | 3 | 4 |
n=4 che è pari per cui ho:
![]() che corrisponde al valore 10.
che corrisponde al valore 10.
![]() che corrisponde al valore 12.
che corrisponde al valore 12.
Adesso trovo la media tra questi due valori che è:
![]()
La moda è il valore che si presenta con maggiore frequenza.
Ad esempio dati i seguenti valori:
5,6,7,7,8.
La moda risulta 7 in quanto è il valore che si presenta con maggior frequenza.[:de]

Rafel Olbinski
La mediana (Me) è quel dato che divide l’insieme dei dati in due parti uguali.
L’idea che è alla base della mediana è quella di cercare un numero che sia più grande di un 50% delle osservazioni e più piccolo del restante 50%.
Spero con un esempio di chiarire il concetto:
Dati i seguenti valori:
71, 81, 90, 92, 94, 96, 97
Per trovare la mediana devo contare i valori che sono 7:
Il valore che sta esattamente nel mezzo è il 92 infatti esso ha alla sua sinistra 3 valori ed alla sua destra altri 3.
Quindi si deve pensare più che al valore di per sé alla sua posizione.
Per determinare quale valore prendere si prende quel valore che si trova alla posizione:
![]()
con n il numero dei valori.
Relazione che vale se il numero di valori è dispari
nel caso dell’esempio il calcolo precedente risulta:
![]()
ossia devo prendere il calore che si trova alla posizione 4 che è appunto il 92.
Inserisco questa tabella per chiarire maggiormente il concetto:
| valore | 71 | 81 | 90 | 92 | 94 | 96 | 97 |
| posizione | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Nel caso in cui invece il numero di valori è pari quale valore prendere?
Si prendono i due valori che stanno nella posizione ![]() e
e ![]() e si fa la loro media.
e si fa la loro media.
Un esempio spero che chiarisca il concetto.
Dati i valori
| Valore | 7 | 10 | 12 | 15 |
| Posizione | 1 | 2 | 3 | 4 |
n=4 che è pari per cui ho:
![]() che corrisponde al valore 10.
che corrisponde al valore 10.
![]() che corrisponde al valore 12.
che corrisponde al valore 12.
Adesso trovo la media tra questi due valori che è:
![]()
La moda è il valore che si presenta con maggiore frequenza.
Ad esempio dati i seguenti valori:
5,6,7,7,8.
La moda risulta 7 in quanto è il valore che si presenta con maggior frequenza.[:]
[:it]

Rafal Olbinski
Razionalizzare significa quindi togliere la radice dal denominatore trovando chiaramente una frazione equivalente.
Tale operazione viene usata molto spesso nel trovare la soluzione delle equazioni di secondi grado e nello studio di funzioni polinomiali o nelle funzioni trigonometriche.
La parte più importante dei radicali è proprio la razionalizzazione che poi è una diretta conseguenza delle proprietà delle potenze.
Inserisco adesso degli esercizi suddivisi per livello.
Per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
![Rendered by QuickLaTeX.com \left [ \cfrac{3\sqrt{15}}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c1fef64c2c870c09c550a985b9df9f75_l3.png) |
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
|
| 6.9. |
|
| 6.10. |
|
| 6.11. |
|
| 6.12. |
[:en]

Rafel Olbinski
Razionalizzare significa quindi togliere la radice dal denominatore trovando chiaramente una frazione equivalente.
Tale operazione viene usata molto spesso nel trovare la soluzione delle equazioni di secondi grado e nello studio di funzioni polinomiali o nelle funzioni trigonometriche.
La parte più importante dei radicali è proprio la razionalizzazione che poi è una diretta conseguenza delle proprietà delle potenze.
Inserisco adesso degli esercizi suddivisi per livello.
Per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
![Rendered by QuickLaTeX.com \left [ \cfrac{3\sqrt{15}}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c1fef64c2c870c09c550a985b9df9f75_l3.png) |
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
|
| 6.9. |
|
| 6.10. |
|
| 6.11. |
|
| 6.12. |
[:de]

Rafel Olbinski
Razionalizzare significa quindi togliere la radice dal denominatore trovando chiaramente una frazione equivalente.
Tale operazione viene usata molto spesso nel trovare la soluzione delle equazioni di secondi grado e nello studio di funzioni polinomiali o nelle funzioni trigonometriche.
La parte più importante dei radicali è proprio la razionalizzazione che poi è una diretta conseguenza delle proprietà delle potenze.
Inserisco adesso degli esercizi suddivisi per livello.
Per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
![Rendered by QuickLaTeX.com \left [ \cfrac{3\sqrt{15}}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c1fef64c2c870c09c550a985b9df9f75_l3.png) |
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
|
| 6.9. |
|
| 6.10. |
|
| 6.11. |
|
| 6.12. |
[:]

Jim Warren
Razionalizzare significa trasformare una frazione in un’altra, ad essa equivalente, senza radicali o al numeratore o al denominatore.
Comunemente si parla di razionalizzazione quando non vi è un radicale al denominatore.
Questa trasformazione si effettua moltiplicando opportunamente sia il numeratore sia il denominatore della frazione per un fattore, diverso da zero, con un’opportuna radice.
Eccone un esempio:
![]()
non si vuole avere ![]() al denominatore.
al denominatore.
Per ottenere il risultato si moltiplica al numeratore ed al denominatore ![]()
e si ottiene:
![]()
e conseguentemente sapendo che:
![]()
quella di partenza diventa:
![]()
[:it]

Jim Warren
Se un numero o una lettera moltiplica una radice e si vuole raggruppare tutto il segno della radice si deve tener conto della seguente relazione:
![]()
Utilizzando la relazione precedente sviluppare adesso i seguenti esercizi suddivisi per livello.
Per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
Per un livello discreto (7):
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
| 7.4. |
|
| 7.5. |
![Rendered by QuickLaTeX.com \left [\sqrt{\cfrac{1}{12}}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7bf62ee257f721d5197f0c02371b95af_l3.png) |
| 7.6. |
|
| 7.7. |
|
| 7.8. |
Per un buon livello (8):
8.1. ![Rendered by QuickLaTeX.com -\cfrac{2}{5}\sqrt[3]{\cfrac{25}{4}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f8eb0a1626f86182bdebb0d0de4211ce_l3.png) |
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{5}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-116d97c34f9ce9c78d11eb68baf7d238_l3.png) |
8.2. ![Rendered by QuickLaTeX.com -\frac{1}{2}\sqrt[3]{\cfrac{40}{3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-16e61c2921dbdbe8e5cf5ab140d9fcbb_l3.png) |
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{5}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-0300581f825606a4df561791b959784d_l3.png) |
8.3. ![Rendered by QuickLaTeX.com -\cfrac{4}{3}\sqrt[3]{\cfrac{9}{32}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-98662ced01fc9c0f6667680cec8b50f0_l3.png) |
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a2e8a6fda45f51f4d757ab599f211f1a_l3.png) |
8.4. ![Rendered by QuickLaTeX.com -\cfrac{3}{4}\sqrt[3]{\cfrac{4}{9}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-32123463fa31c8f9543ab093139135c6_l3.png) |
![Rendered by QuickLaTeX.com \left [ -\sqrt[3]{\cfrac{3}{16}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3081a84110f7fbcd3efe5cd77db53175_l3.png) |
8.5. ![Rendered by QuickLaTeX.com \cfrac{2}{3}\sqrt[2]{2-\cfrac{7}{8}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3a2cce9a34148ff74aabc3a10a539306_l3.png) |
|
8.6. 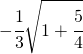 |
|
| 8.7. |
|
8.8. 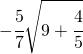 |
Per un livello quasi ottimo (9)
| 9.1. |
[:en]

Jim Warren
Se un numero o una lettera moltiplica una radice e si vuole raggruppare tutto il segno della radice si deve tener conto della seguente relazione:
![]()
Utilizzando la relazione precedente sviluppare adesso i seguenti esercizi suddivisi per livello
Per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
Per un livello discreto (7):
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
| 7.4. |
|
| 7.5. |
![Rendered by QuickLaTeX.com \left [\sqrt{\cfrac{1}{12}}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7bf62ee257f721d5197f0c02371b95af_l3.png) |
| 7.6. |
|
| 7.7. |
|
| 7.8. |
Per un buon livello (8):
8.1. ![Rendered by QuickLaTeX.com -\cfrac{2}{5}\sqrt[3]{\cfrac{25}{4}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f8eb0a1626f86182bdebb0d0de4211ce_l3.png) |
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{5}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-116d97c34f9ce9c78d11eb68baf7d238_l3.png) |
8.2. ![Rendered by QuickLaTeX.com -\frac{1}{2}\sqrt[3]{\cfrac{40}{3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-16e61c2921dbdbe8e5cf5ab140d9fcbb_l3.png) |
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{5}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-0300581f825606a4df561791b959784d_l3.png) |
8.3. ![Rendered by QuickLaTeX.com -\cfrac{4}{3}\sqrt[3]{\cfrac{9}{32}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-98662ced01fc9c0f6667680cec8b50f0_l3.png) |
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a2e8a6fda45f51f4d757ab599f211f1a_l3.png) |
8.4. ![Rendered by QuickLaTeX.com -\cfrac{3}{4}\sqrt[3]{\cfrac{4}{9}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-32123463fa31c8f9543ab093139135c6_l3.png) |
![Rendered by QuickLaTeX.com \left [ -\sqrt[3]{\cfrac{3}{16}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3081a84110f7fbcd3efe5cd77db53175_l3.png) |
8.5. ![Rendered by QuickLaTeX.com \cfrac{2}{3}\sqrt[2]{2-\cfrac{7}{8}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3a2cce9a34148ff74aabc3a10a539306_l3.png) |
|
8.6. 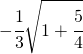 |
|
| 8.7. |
|
8.8. 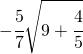 |
Per un livello quasi ottimo (9)
| 9.1. |
[:de]

Jim Warren
Se un numero o una lettera moltiplica una radice e si vuole raggruppare tutto il segno della radice si deve tener conto della seguente relazione:
![]()
Utilizzando la relazione precedente sviluppare adesso i seguenti esercizi suddivisi per livello
Per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
Per un livello discreto (7):
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
| 7.4. |
|
| 7.5. |
![Rendered by QuickLaTeX.com \left [\sqrt{\cfrac{1}{12}}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7bf62ee257f721d5197f0c02371b95af_l3.png) |
| 7.6. |
|
| 7.7. |
|
| 7.8. |
Per un buon livello (8):
8.1. ![Rendered by QuickLaTeX.com -\cfrac{2}{5}\sqrt[3]{\cfrac{25}{4}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f8eb0a1626f86182bdebb0d0de4211ce_l3.png) |
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{5}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-116d97c34f9ce9c78d11eb68baf7d238_l3.png) |
8.2. ![Rendered by QuickLaTeX.com -\frac{1}{2}\sqrt[3]{\cfrac{40}{3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-16e61c2921dbdbe8e5cf5ab140d9fcbb_l3.png) |
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{5}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-0300581f825606a4df561791b959784d_l3.png) |
8.3. ![Rendered by QuickLaTeX.com -\cfrac{4}{3}\sqrt[3]{\cfrac{9}{32}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-98662ced01fc9c0f6667680cec8b50f0_l3.png) |
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a2e8a6fda45f51f4d757ab599f211f1a_l3.png) |
8.4. ![Rendered by QuickLaTeX.com -\cfrac{3}{4}\sqrt[3]{\cfrac{4}{9}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-32123463fa31c8f9543ab093139135c6_l3.png) |
![Rendered by QuickLaTeX.com \left [ -\sqrt[3]{\cfrac{3}{16}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3081a84110f7fbcd3efe5cd77db53175_l3.png) |
8.5. ![Rendered by QuickLaTeX.com \cfrac{2}{3}\sqrt[2]{2-\cfrac{7}{8}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3a2cce9a34148ff74aabc3a10a539306_l3.png) |
|
8.6. 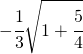 |
|
| 8.7. |
|
8.8. 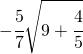 |
Per un livello quasi ottimo (9)
| 9.1. |
[:]

Vladimir Kush
Per sviluppare questi esercizi ricordo questi tre teoremi:
2. ![Rendered by QuickLaTeX.com \cfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\cfrac{a}{b}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-72a4779832adecc9db54627aff579e61_l3.png)
3. ![]()
Esercizi per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
|
| 6.9. |
|
| 6.10. |
|
| 6.11. |
|
| 6.12. |
|
| 6.12. |
|
| 6.13. |
Esercizi per un livello discreto (7):
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
| 7.4. |
|
| 7.5. |
|
| 7.6. |
![Rendered by QuickLaTeX.com \left [ \sqrt[3]{\cfrac{3}{16}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-26c97c3c1e73806b4efe438114e712dc_l3.png) |
| 7.7. |
|
7.8. ![Rendered by QuickLaTeX.com \sqrt[4]{\cfrac{9a^2b^4}{16c^6}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f10b03216b38445efffe2dd12bd5369f_l3.png) |
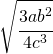 |
Esercizi per un buon livello
8.1. ![Rendered by QuickLaTeX.com \sqrt[4]{\cfrac{9}{16}+\cfrac{3}{2}+1}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-faee1149f7b9e8ae04313342cb2e71f2_l3.png) |
|
8.2. ![Rendered by QuickLaTeX.com \sqrt[6]{\cfrac{25}{9}-\cfrac{10}{3}+1}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-728aac4ec645636813f7a66481d305f6_l3.png) |
|
8.3. ![Rendered by QuickLaTeX.com \sqrt[2]{\cfrac{9}{49}+\cfrac{12}{7}+4}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-057c824034125a2021e9350be7484684_l3.png) |
Esercizi per un livello quasi ottimo (9)
| 9.1. |
|
| 9.2. |
Per un livello ottimo (10)
10.1. ![Rendered by QuickLaTeX.com \sqrt[6]{\cfrac{x^2-10x+25}{x^2-8xy+16y^2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f64a34efd752c1499f92daa202280468_l3.png) |
![Rendered by QuickLaTeX.com \left [\sqrt[3]{\cfrac{x-5}{x-4y}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c36847a763bf12a84b44dd7b03aa530e_l3.png) |
10.2. ![Rendered by QuickLaTeX.com \sqrt[9]{\cfrac{27a^3b^6}{\left ( 81a^2-18a+1 \right )^3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-25f05ba22d0f46215979fa4ec827a23e_l3.png) |
![Rendered by QuickLaTeX.com \left [ \cfrac{3ab^2}{\left ( 9a-1 \right )^2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-22dadf3866a664b2c64062d013cdfc69_l3.png) |

Jim Warren
La media aritmetica è quel valore che un evento avrebbe se non esistesse la variabilità.
Nel caso dei voti a scuola, se si prendesse sempre 6 la media sarebbe 6 ma essendoci la variabilità ossia anche altri voti non è detto che la media alla fine risulti 6.
Dal punto di vista aritmetico si calcola la media nella seguente maniera:
![]()
dove ![]() sono gli eventi e
sono gli eventi e ![]() è il numero di eventi.
è il numero di eventi.
Riprendendo l’esempio dei voti a scuola.
Alla fine di un anno scolastico si hanno i seguenti voti:
6,7,8.
La media risulta:
![]()
Nel caso in cui avessi i seguenti voti:
si prendono quattro 6, tre 7, cinque 8, e devo calcolare la media.
Si usa la media ponderata o pesata che tiene conto del numero di volte in cui è capitato l’evento.
![]()

Jim Warren
Descrivere un insieme di cose in maniera sintetica è una caratteristica spontanea dell’uomo: quante sono le macchine rosse, quanti uomini o donne vi sono in un gruppo, quante sono le materie in un anno scolastico, com’è il rendimento scolastico.
Ad esempio se voglio una descrizione della tipologia di persone che frequentano un ristorante, ho bisogno di strumenti affinché possa poi capire che tipo di cucina o che alimenti debba comprare.
Cerco di partire da un esempio: i voti presi durante un anno scolastico.
6, 5, 4, 6, 7,6,5,
Il primo parametro è la frequenza.
Si definisce frequenza assoluta il numero di volte che quel particolare evento si ripete.
Nel caso dell’esempio precedente ho:
| Evento | frequenza assoluta |
| 6 | 3 |
| 5 | 2 |
| 4 | 1 |
| 7 | 1 |
| Totale | 7 |
La frequenza relativa invece è la frequenza assoluta espressa in percentuale rispetto al totale dell’evento.
| evento | frequenza assoluta | frequenza relativa |
| 6 | 3 | |
| 5 | 2 | |
| 4 | 1 | |
| 7 | 1 | |
| totale | 7 | 100% |
Conoscere la frequenza con cui un evento si ripete è fondamentale per far fronte a quell’evento più probabile in maniera migliore. Ad esempio se la frequenza dei clienti che chiedono una pizza margherita è superiore a quella di coloro che chiedono una pizza alla verdure dovrò acquistare meno verdure.