[:it]

Joel Rea
L’ellisse è quel luogo dei punti del piano per cui è costante la somma delle distanze da due punti fissi detti fuochi.
L’ellisse rappresenta ad esempio il percorso dei pianeti attorno al Sole, la forma stessa della Terra è ellittica, un uovo è ellittico, lo stesso cerchione di un pneumatico se non perfettamente rotondo viene rappresentato da un’ellisse.
Come nelle precedenti forme geometriche anche l’ellisse ha un’equazione che la rappresenta.
![]()
Se due fuochi dell’ellisse hanno coordinate:
![]()
allora ![]()
![]()
e l’ellisse ha questa rappresentazione grafica
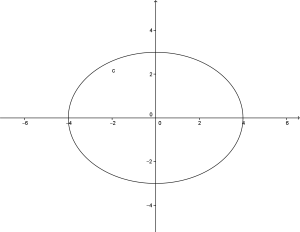
Se invece i due fuochi delle ellisse hanno coordinate:
![]()
allora ![]()
![]()
e l’ellisse ha questa rappresentazione grafica:
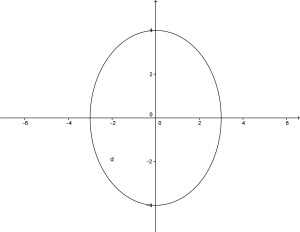 ma la
ma la ![]() e la
e la ![]() cosa rappresentano?
cosa rappresentano?
Danno la lunghezza dei semiassi dell’ellisse.
In pratica l’ellisse è racchiusa in un rettangolo i cui lati sono ![]() e
e ![]() .
.
Ossia si ha una figura del genere:
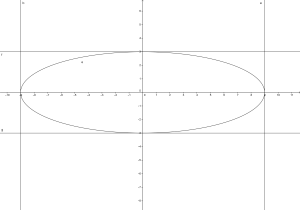 ma cosa differisce un’ellisse da una circonferenza?
ma cosa differisce un’ellisse da una circonferenza?
Dall’eccentricità ossia di quanto essa è schiacciata rispetto o l’asse x o l’asse y.
in pratica l’eccentricità è un rapporto tra la coordinata dei fuochi e l’asse maggiore dell’ellisse.
![]()
Nel caso della circonferenza ![]() per cui
per cui ![]() ed, infatti, l’eccentricità è nulla.[:en]
ed, infatti, l’eccentricità è nulla.[:en]

Joel Rea
L’ellisse è quel luogo dei punti del piano per cui è costante la somma delle distanze da due punti fissi detti fuochi.
L’ellisse rappresenta ad esempio il percorso dei pianeti attorno al Sole, la forma stessa della Terra è ellittica, un uovo è ellittico, lo stesso cerchione di un pneumatico se non perfettamente rotondo viene rappresentato da un’ellisse.
Come nelle precedenti forme geometriche anche l’ellisse ha un’equazione che la rappresenta.
![]()
Se due fuochi dell’ellisse hanno coordinate:
![]()
allora ![]() e l’ellisse ha questa rappresentazione grafica
e l’ellisse ha questa rappresentazione grafica

Se invece i due fuochi delle ellisse hanno coordinate:
![]()
allora ![]()
e l’ellisse ha questa rappresentazione grafica:
 ma la
ma la ![]() e la
e la ![]() cosa rappresentano?
cosa rappresentano?
Danno la lunghezza dei semiassi dell’ellisse.
In pratica l’ellisse è racchiusa in un rettangolo i cui lati sono ![]() e
e ![]() .
.
Ossia si ha una figura del genere:
 ma cosa differisce un’ellisse da una circonferenza?
ma cosa differisce un’ellisse da una circonferenza?
Dall’eccentricità ossi di quanto essa è schiacciata rispetto o l’asse x o l’asse y.
in pratica l’eccentricità è un rapporto tra la coordinata dei fuochi e l’asse maggiore dell’ellisse.
![]()
Nel caso della circonferenza ![]() per cui
per cui ![]() ed, infatti, l’eccentricità è nulla.[:de]
ed, infatti, l’eccentricità è nulla.[:de]
Die Ellipse
Eine Ellipse kann definiert werden als die Menge aller Punkte der Ebene, für die die Summe der Abstände zu zwei gegebenen Punkten und gleich einer gegebenen Konstante ist. Die Punkte und heißen Brennpunkte.
Die Ellipse repräsentiert zum Beispiel den Kurs von den Planeten um die Sonne, die gleiche Form von der Erde ist elliptisch, ein Ei ist elliptisch, Felgen von einem Reifen, wenn es nicht genau rund ist spricht man von einer Ellipse.
Wie auch die vorhergehenden geometrischen Formen wird die Ellipse durch eine Gleichung dargestellt.
Wenn zwei Brennpunkte der Ellipse Koordinaten haben,
hat die Ellipse diese grafische Darstellung
Wenn die Brennpunkte hingegen folgende Koordinaten haben,
hat die Ellipse diese grafische Darstellung
aber was stellen a und b dar?
Sie geben die Länge der Halbachsen der Ellipse an.
In der Praxis ist die Ellipse in einem Rechteck enthalten, dessen Seiten 2a und 2b sind.
Oder wir haben eine Form dieser Art:
Aber was unterscheidet eine Ellipse von einem Umfang?
Entweder die Exzentrizität oder wieviel die Ellipse hinsichtlich der Achse x oder y zerquetscht ist.
Die Exzentrizität ist also eine Beziehung zwischen der Koordinate der Brennpunkte und der größten Achse der Ellipse.
Wenn der Umfang a=b bzw. C=0, ist die Exzentrizität null.
[:]




![Rendered by QuickLaTeX.com \left [ \cfrac{3\sqrt{15}}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c1fef64c2c870c09c550a985b9df9f75_l3.png)


![Rendered by QuickLaTeX.com \left [\sqrt{\cfrac{1}{12}}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7bf62ee257f721d5197f0c02371b95af_l3.png)
![Rendered by QuickLaTeX.com -\cfrac{2}{5}\sqrt[3]{\cfrac{25}{4}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f8eb0a1626f86182bdebb0d0de4211ce_l3.png)
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{5}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-116d97c34f9ce9c78d11eb68baf7d238_l3.png)
![Rendered by QuickLaTeX.com -\frac{1}{2}\sqrt[3]{\cfrac{40}{3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-16e61c2921dbdbe8e5cf5ab140d9fcbb_l3.png)
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{5}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-0300581f825606a4df561791b959784d_l3.png)
![Rendered by QuickLaTeX.com -\cfrac{4}{3}\sqrt[3]{\cfrac{9}{32}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-98662ced01fc9c0f6667680cec8b50f0_l3.png)
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a2e8a6fda45f51f4d757ab599f211f1a_l3.png)
![Rendered by QuickLaTeX.com -\cfrac{3}{4}\sqrt[3]{\cfrac{4}{9}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-32123463fa31c8f9543ab093139135c6_l3.png)
![Rendered by QuickLaTeX.com \left [ -\sqrt[3]{\cfrac{3}{16}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3081a84110f7fbcd3efe5cd77db53175_l3.png)
![Rendered by QuickLaTeX.com \cfrac{2}{3}\sqrt[2]{2-\cfrac{7}{8}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3a2cce9a34148ff74aabc3a10a539306_l3.png)
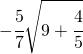

![Rendered by QuickLaTeX.com \cfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\cfrac{a}{b}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-72a4779832adecc9db54627aff579e61_l3.png)
![Rendered by QuickLaTeX.com \left [ \sqrt[3]{\cfrac{3}{16}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-26c97c3c1e73806b4efe438114e712dc_l3.png)
![Rendered by QuickLaTeX.com \sqrt[4]{\cfrac{9a^2b^4}{16c^6}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f10b03216b38445efffe2dd12bd5369f_l3.png)
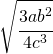
![Rendered by QuickLaTeX.com \sqrt[4]{\cfrac{9}{16}+\cfrac{3}{2}+1}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-faee1149f7b9e8ae04313342cb2e71f2_l3.png)
![Rendered by QuickLaTeX.com \sqrt[6]{\cfrac{25}{9}-\cfrac{10}{3}+1}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-728aac4ec645636813f7a66481d305f6_l3.png)
![Rendered by QuickLaTeX.com \sqrt[2]{\cfrac{9}{49}+\cfrac{12}{7}+4}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-057c824034125a2021e9350be7484684_l3.png)
![Rendered by QuickLaTeX.com \sqrt[6]{\cfrac{x^2-10x+25}{x^2-8xy+16y^2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f64a34efd752c1499f92daa202280468_l3.png)
![Rendered by QuickLaTeX.com \left [\sqrt[3]{\cfrac{x-5}{x-4y}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c36847a763bf12a84b44dd7b03aa530e_l3.png)
![Rendered by QuickLaTeX.com \sqrt[9]{\cfrac{27a^3b^6}{\left ( 81a^2-18a+1 \right )^3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-25f05ba22d0f46215979fa4ec827a23e_l3.png)
![Rendered by QuickLaTeX.com \left [ \cfrac{3ab^2}{\left ( 9a-1 \right )^2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-22dadf3866a664b2c64062d013cdfc69_l3.png)



![Rendered by QuickLaTeX.com \left[\cfrac{7}{x+2}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-54046183c8ce402bd873f3fe1da73dcd_l3.png)
![Rendered by QuickLaTeX.com \left[\cfrac{6x}{x+2y}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-25e15a79e3953112dfde74a771ae9a83_l3.png)
![Rendered by QuickLaTeX.com \left[\cfrac{2a}{a+1}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-87dc784053b1a3af04255d5559c124c5_l3.png)
![Rendered by QuickLaTeX.com \left[\cfrac{1-x}{a-x^2}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e3191b1f9c9d953f51225a43cc7645b1_l3.png)