[:it]
[WpProQuiz 38]
[:]

[:it]
Ogni numero deve essere pensato con il suo segno ossia + o -.
Tale notazione ha numerose applicazioni:
Come si effettuano le operazioni con i numeri relativi.
S O M M A
Se i due numeri hanno lo stesso segno si sommano le cifre e si prende il segno uguale
es: -8 -2 = – 10 ossia prendo 8 + 2 = 10 e metto il segno comune ossia il – ed appunto -10
Se i due numeri hanno segno opposto prendo il più grande e vi sottraggo il più piccolo prendendo sempre il segno del più grande
esempio
-8 + 2
esempio
+10 -2
M O L T I P L I C A Z I O N E / D I V I S I O N E
Bisogna ricordarsi la seguente regola:
![]()
![]()
![]()
![]()
Prima si stabilisce il segno risultante della moltiplicazione seguendo la tabella precedente e poi si esegue la normale moltiplicazione tra le cifre
esempio
![]()
esempio
![]()
esempio
![]()
esempio
![]()
CONFRONTO TRA NUMERI RELATIVI
Per valutare che un numero relativo sia più grande di un altro si deve confrontare il segno; se segni opposti il numero con il segno negativo è sempre minore; se di segno uguale si hanno due casi:
ATTENZIONE
Il segno minore è <
il segno maggiore è >
[:]
[:it]
Per esercitarsi sull’approssimazione per arrotondamento.
Per un livello base [6]
Approssimare alla prima cifra decimale:
| 6.1. 3,56 | |
| 6.2. 5,67 | |
| 6.3. 2,67 | |
| 6.4. 2,12 | |
| 6.5. 6.89 | |
| 6.6. 8,90 | |
| 6.7. 3,98 | |
| 6.8. 4,76 | |
| 6.9. 6,45 | |
| 6.10. 9,87 |
Approssimare alla seconda cifra decimale [7]
| 7.1. 2,345 | |
| 7.2. 4,567 | |
| 7.3. 4,009 | |
| 7.4. 4,987 | |
| 7.5. 7,765 | |
| 7.6. 3,123 | |
| 7.7. 9,654 | |
| 7.8. 10,543 | |
| 7.9. 12,345 | |
| 7.10. 23,678 |
Esercizi per un livello per maggiore sicurezza [8]
Calcolare il risultato con la seconda cifra decimale
| 8.1. il 12% di 15,69€ | |
| 8.2. il 22% di 34,99e | |
| 8.3. il 22% di 20€ | |
| 8.4. il 22% di 56,99 | |
| 8.5. 1,456€ per 34 | |
| 8.6. 4,45€ diviso 12 | |
| 8.7. 5,66€ diviso 13 | |
| 8.8. 7,8 diviso 25 | |
| 8.9. 4,567 + 4,678 | |
| 8.10. 5,678 + 10,456 |
[:]
[:it]
Nei conti bancari, nel prezzo della benzina, nel calcolo dell’IVA, nel calcolo delle percentuali, si utilizza moltissimo l’approssimazione per troncamento.
Tale procedura implica la necessità di sapere delle semplici regole che permettono di approssimare la cifra con una certa approssimazione.
La regola è la seguente:
Se il numero è > o uguale a 5 lo si approssima all’unità successiva,
se il numero è < (minore) di cinque si tiene la cifra ottenuta.
Ad esempio:
5,678 approssimato alla seconda cifra decimale diventa 5,68 perché la terza cifra decimale è 8 e quindi si approssima la seconda alla cifra successiva.
5,674 approssimato alla seconda cifra decimale diventa 5,67 perché la terza cifra decimale è 4 e quindi la seconda cifra decimale rimane invariata.
Applicazione ad esempio nel calcolo del costo di 35 litri di benzina:
Oggi il prezzo della benzina è di 1,465 ,si riempie il serbatoio di 35 litri
![]()
Si paga in euro ossia fino alla seconda cifra decimale.
Quanto si pagherà?
51,28 perché la terza cifra è 5 e si approssima per arrotondamento la seconda cifra.
Si deve aumentare il costo di un paio di pantaloni del 22% in quanto l’IVA è applicata su tutti i beni.
Il costo di un paio di pantaloni è di 35,54€ a cui si deve aggiungere il 22% e viene
43,3588, siccome si deve approssimare alla seconda cifra decimale, il costo di un paio di pantaloni diventa:
43,36€.[:]
[:it]
Oltre che l’estrazione di dati dal database (interrogazione), la cancellazione di opportuni record, si ha la necessità di modificare un insieme di record ad esempio questa esigenza può nascere dal fatto il nome di una via è stato cambiato e tutti gli abitanti di questa via devono cambiare il loro indirizzo all’anagrafe del comune.
Per fare questo non si può di certo andare su ogni record e modificare a mano il database.
Per eseguire tale cosa si esegue il seguente comando
UPDATE Anagrafica SET NomeVia =’Via Nuova’
WHERE NomeVia = ‘Via Vecchia’
Dove Anagrafica è il nome della tabella e NomeVia è il nome della colonna di cui si vuole aggiornare il valore.[:]
[:it]
E’ dato lo schema relazionale costituito dalle seguenti tabelle:
(le chiavi primarie sono sottolineate)
SALA RIUNIONE(CodiceSala, CodiceSede, NomeSala)
SEDE(CodiceSede, Nome, Indirizzo, Citta, Stato)
Si sarà creata la seguente relazione:
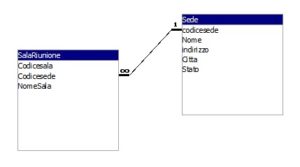 Adesso popolare il database con i seguenti dati:
Adesso popolare il database con i seguenti dati:
| codicesede | Nome | indirizzo | Citta | Stato |
|---|---|---|---|---|
| 1 | Centro Congressi | Via dell’industria 15 | Bolzano | Italia |
| 2 | Centro Belle Speranze | Via della Fede 23 | Vienna | Austria |
| 3 | Centro Pecchi | Via XXVI Ottore | New York | Stati Uniti |
| Codicesala | Codicesede | NomeSala |
|---|---|---|
| 1 | 1 | Sala Verde |
| 2 | 1 | Sala Rossa |
| 3 | 1 | Sala Gialla |
| 4 | 1 | Sala Grande |
| 5 | 2 | Sala Kaiser |
| 6 | 2 | Sala Sissi |
| 7 | 2 | Sala Franz |
| 8 | 2 | Sala Imperatore |
| 9 | 3 | Sala Washington |
| 10 | 3 | Sala Kennedy |
eseguire adesso le seguenti query e dare il seguente nome query# con # il relativo punto
[:]
[:it]
Oltre che estrarre dei valori, spesso si vuole anche cancellarli.
Per poter fare questa operazione valgono tutte le regole della clausola WHERE
Ad esempio il seguente comando cancella tutti i record talla tabella Gioco.
delete from Gioco
Se la tabella gioco contiene i seguenti record:
| IDgioco | Nomegioco |
|---|---|
| 5 | monopoli |
| 6 | scacchi |
| 7 | dama |
si vuole cancellare solo il record che contiene il gioco della dama si deve eseguire la seguente query.
DELETE FROM GIOCO WHERE nomegioco = ‘dama’[:]
[:it]
Spesso, da una tabella si richiedono dei raggruppamenti, sapere la somma di colonne numeriche, sapere quante colonne fanno parte di una tabella.
Ad esempio riprendendo l’esempio degli alunni di una classe del post Join, si vuole sapere quanti sono gli alunni di una classe.
COMANDO GROUP BY e COUNT(*)
Bisogna raggrupparli per classe e contare quanti sono.
In una scuola vi sono molti alunni e molte classi per cui il conto manuale sarebbe improponibile e fonte di numerosi errori.
Il comando per sapere quanti sono gli alunni di una classe risulta il seguente:
SELECT
count(*)
FROM
anagrafica
GROUP By id_classe
L’esito della query precedente fornisce il seguente risultato:
| Expr1000 |
|---|
| 4 |
| 3 |
Come si nota una query del genere ha poco significato ed è di difficile lettura allora voglio anche il nome della classe di cui si vuole conoscere il numero degli studenti.
La query, indubbiamente complessa è la seguente:
SELECT
classe.nome,
count(*)
FROM
anagrafica,
classe
WHERE
anagrafica.id_classe=classe.id_classe
GROUP BY anagrafica.id_classe, classe.nome;
Riflessioni su questa query:
all’interno del comando Group by si deve mettere sia l’id_classe che il nome della classe ossia le stesse colonne che compaiono nella SELECT.
L’esito è il seguente:
| nome | Expr1001 |
|---|---|
| Prima | 4 |
| Seconda | 3 |
Adesso l’esito è indubbiamente migliore ma non ancora il massimo!
Il nome delle colonne non è chiarissimo ma voglio dare un nome più coerente con il suo contenuto.
AS
Il comando AS permette di rinominare una colonna.
Nel caso della query precedente si ha:
SELECT
classe.nome AS classe,
Count(*) AS studenti
FROM
anagrafica,
classe
WHERE
anagrafica.id_classe=classe.id_classe
GROUP BY classe.nome, anagrafica.id_classe;
SUM
Supponiamo adesso che ogni studente abbia versato una quota per la partecipazione della gita e voglio sapere il totale della cifra a disposizione.
Naturalmente la tabella Anagrafica deve contemplare adesso la colonna quota all’interno della quale si è inserita la cifra versata dal relativo studente.
La tabella anagrafica contiene i seguenti dati:
| ID_anagrafica | nome | id_classe | quota |
|---|---|---|---|
| 1 | Paolo | 1 | € 41,00 |
| 2 | Filippo | 1 | € 32,00 |
| 3 | Maria | 1 | € 25,00 |
| 4 | Giovanna | 1 | € 32,00 |
| 5 | Tommaso | 2 | € 52,00 |
| 6 | Marta | 2 | € 12,00 |
| 7 | Giovanna | 2 | € 12,00 |
La query sarà la seguente:
SELECT
SUM(quota) AS TOTALE
from anagrafica
WHERE
id_classe=1;
che fornisce come risultato:
| TOTALE |
|---|
| € 130,00 |
AVG
Se voglio conoscere il valore medio della quota versata dai singoli ragazzi si deve eseguire la seguente query.
SELECT
AVG(quota) AS media
from anagrafica
WHERE
id_classe=1;
che fornisce come risultato:
| MEDIA |
|---|
| € 32,50 |
[:]