[:it]

Roberto Bergonzo
[WpProQuiz 44][:]

[:it]

Roberto Bergonzo
[WpProQuiz 44][:]
[:it]

Francis Picabia
Rappresenta graficamente 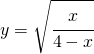 e determina l’area della regione di piano compresa fra la curva, l’asse delle y e la retta tangente alla curva nel suo punto di flesso. (suggerimento. Per il calcolo dell’integrale poni
e determina l’area della regione di piano compresa fra la curva, l’asse delle y e la retta tangente alla curva nel suo punto di flesso. (suggerimento. Per il calcolo dell’integrale poni ![]() ).
).
Sviluppo.
Intanto rappresento graficamente la curva.
Per calcolare il dominio si deve porre l’argomento della radice ![]() ed il denominatore
ed il denominatore ![]() .
.
![]()
Il numeratore è positivo per
![]()
il denominatore non può essere negativo per cui ho:
![]()
ossia
![]()
unendo le due disequazioni e valutando il segno si ha:
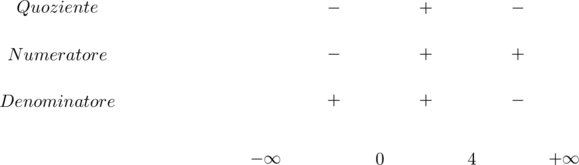
Quindi il dominio è:
![]()
Presenta un asintoto verticale in ![]() e, sempre usando lo studio del segno della funzione:
e, sempre usando lo studio del segno della funzione:
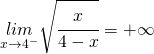
Adesso bisogna fare la derivata prima e successivamente la derivata seconda per determinare il punto di flesso e l’equazione della retta in esso tangente.
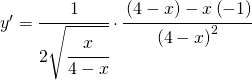
semplificandola opportunamente si ha:
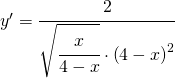
per trovare il flesso devo calcolare la derivata seconda.
Per comodità riscrivo la derivata prima nella seguente maniera:
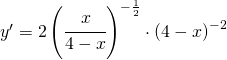
la derivata seconda deve essere posta a zero per trovare il punto di flesso.
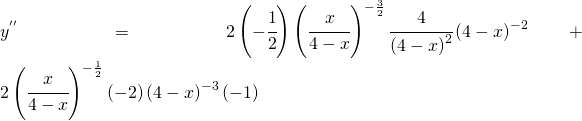
semplificandola in maniera opportuna essa diventa:
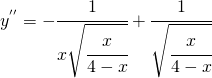
che si annulla per ![]()
Sostituendo il valore trovato alla funzione di partenza 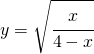
![]()
Le coordinate del punto di flesso sono:
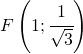
per trovare il coefficiente angolare della retta passante per il punto di flesso è sufficiente calcolare il valore della derivata prima in ![]()
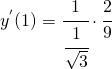
![]()
La retta tangente alla curva e passante per il punto di flesso ha equazione:
![]()
Rappresento sul piano cartesiano la curva e la retta.
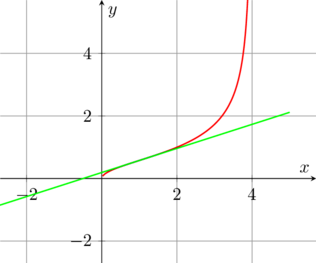
Per meglio capire la zona di cui si deve calcolare l’area evidenzio solo la zona di interesse ossia per ![]()
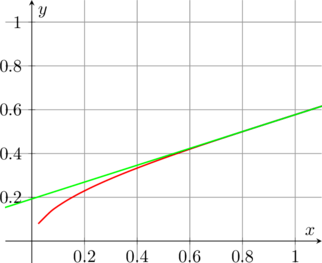
L’area voluta è quel piccolo spicchio tra l’asse y la retta e la curva per cui si dovranno calcolare i seguenti integrali:
(1) 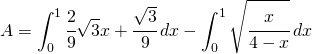
Il primo integrale è facilmente risolvibile
(2) ![]()
La seconda parte dell’integrale chiede la seguente sostituzione ![]() , derivando
, derivando
![]()
cambiando gli estremi di integrazione, in seguito alla sostituzione:
![]()
risolta dà
![]()
e
![]()
![]()
prendo solo la radice positiva
![]()
![]()
diventa:
(3) 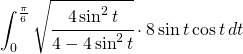
ricordandosi l’equazione goniometrica:
![]() ed applicandola al denominatore della (3)
ed applicandola al denominatore della (3)
![]()
la (3) diventa:
(4) 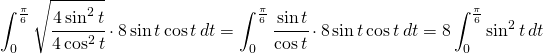
La primitiva si può calcolare attraverso l’integrazione per parti.
![]()
utilizzando sempre l’equazione goniometrica
![]()
spostando al primo membro i due integrali si ha:
![]()
e l’integrale risolto diventa:
![]()
(5) ![]()
Adesso sottraendo alla (2) la (5) si ha il risultato:
![]()
[Questo post è interamente scritto in LaTex]
[:]
[:it]

Francis Picabia
Due rette sono parallele quando hanno lo stesso coefficiente angolare.
Ossia hanno lo stesso numero che moltiplica la ![]() .
.
Ad esempio
![]()
![]()
![]()
![]()
sono tutte rette parallele ed infatti dal grafico lo si vede
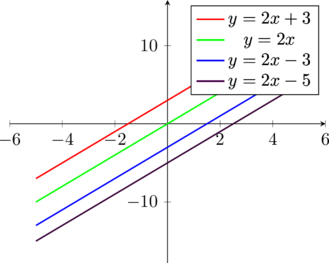
Due rette sono perpendicolari quando il coefficiente angolare è opposto e reciproco uno all’altro.
Ad esempio
![]()
![]()
sono rette perpendicolari ed infatti dal grafico lo si può notare:
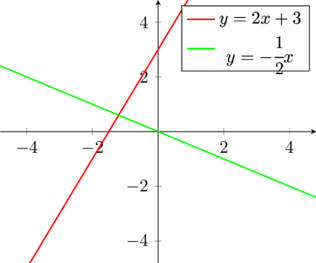
[Questo post è scritto totalmente in LaTex]
[:]
[:it] 9.1.
9.1. ![]()
Effettuo la seguente sostituzione:
(1) ![]()
![]()
elevo entrambi i membri alla seconda in maniera da non avere più la radice quadrata
![]()
![]()
![]()
![]()
facendo la derivata a desta e sinistra si ha:
![]()
(2) ![]()
![]()
(3) ![]()
Adesso sostituendo la (2) e la (3) nell’integrale di partenza si ha:
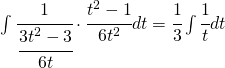
![]()
e sostituendo la (1) si ha come risultato:
![]() [:]
[:]
[:it]

Renè Magritte
Esercizi per un livello sufficiente [6]
| 6.1. |
|
| 6.2. |
Esercizi per un livello discreto [7]
| 7.1. |
|
Esercizi per un livello ottimo[9/10]
| 9.1. |
[:it]

Renè Magritte
Gli integrali per sostituzione utilizzano il cambio o sostituzione di variabile per trovarsi in una situazione di più semplice risoluzione.
Tale metodo può sempre essere applicato a qualunque tipo di integrale sempre che tale sostituzione possa poi portare ad un integrale facilmente sviluppabile.
La cosa fondamentale è la seguente:
![]()
e quindi
![]()
![]()
Ad esempio tale metodo può essere applicato al seguente integrale:
![]()
pongo ![]()
effettuo la derivata a destra e a sinistra
![]()
![]()
Adesso sostituisco nell’integrale che diventa:
![]()
ma ![]()
ed il risultato diventa:
![]()
Sostituzioni più comuni:
| Integrale | Sostituzione |
[:]
[:it]

George Grie
Esercizi per un livello sufficiente [6]
Calcolare le seguenti potenze
| 6.1. |
|
6.2. 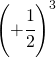 |
|
6.3. 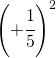 |
|
| 6.4. |
|
| 6.5. |
|
6.6. 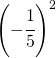 |
|
6.7. 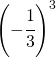 |
|
6.8. 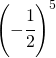 |
|
| 6.9. |
|
6.10. 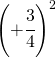 |
|
6.11. 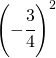 |
Stabilire solo il segno delle seguenti potenze
| Potenza | Segno | Potenza | Segno |
| + | |||
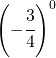 |
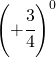 |
||
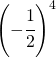 |
|||
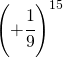 |
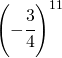 |
||
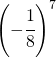 |
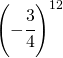 |
||
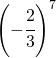 |
|||
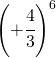 |
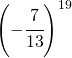 |
||
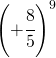 |
[:]
[:it]

George Grie
Per sviluppare la potenza dei numeri relativi si richiamano le proprietà delle potenze con questa aggiunta:
ogni potenza di base positiva è sempre positiva ad esempio
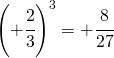
mentre ogni potenza di base negativa:
Esempio
esponente pari e base negativa –> risultato sempre positivo
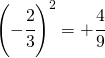
esponente dispari e base negativa –> risultato sempre negativo
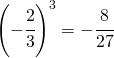 [:]
[:]