SCIENZE E TECNOLOGIE INFORMATICHE

[:it]Anno2015

Anno2017[:]

[:it]

Vladimir Kush

La lunghezza media di un codice è data da quanti simboli in media sono necessari per mandare un messaggio con tali simboli ossia:

dove con è il numero di simboli.

oppure se si conosce la lunghezza del codice:

Per efficienza si intende:

Per ridondanza si intende quindi

ossia quanto più una sorgente ha una grande entropia (ossia fornisce molte informazioni) con un alfabeto molto basso, minore è la ridondanza ossia la necessità di trasmettere segnali simili nel canale trasmissivo.[:]

[:it]

Vladimir Kush

Che cos’è l’entropia di una sorgente?

E’ il massimo grado di informazione che può darci un opportuno codice.

In fisica l’entropia fornisce il grado di disordine di un particolare sistema, nella teoria dell’informazione quanto più un codice ha un’elevata entropia quanta più informazione esso potrà portare.

Nella teoria della probabilità, quando due eventi sono statisticamente indipendenti la probabilità che uno accada in seguito all’altro è dato dal prodotto delle loro probabilità ossia: (principio delle probabilità composte)

L’unica funzione matematica che dal prodotto permette di passare alla somma è ancora il logaritmo per cui esso compare ancora nella definizione di entropia:

L’unità di misura dell’entropia è il bit/carattere.

La velocità di trasmissione viene definita non come la frequenza con cui si trasmette ma come il prodotto tra l’entropia e la frequenza dei simboli emessi.[:]

[:it]

Vladimir Kush

L’informazione, nell’ambito delle telecomunicazioni,  viene definita come la riduzione di incertezza che si poteva avere a priori sul simbolo trasmesso.

Sembra un panegirico ma, in realtà, il concetto è che se io trasmetto sempre un solo segnale sempre uguale, la probabilità di riceverlo è sempre 1. Ma tale fatto significa anche che l’informazione trasmessa è nulla.

Per trasmettere un’informazione vi è bisogno che si modifichi uno stato da luce a buio o viceversa; si pensi ai solo caratteri morse: per comunicare un messaggio, ossia un’informazione, si alternano i punti con le linee in un’opportuna combinazione.

Per dare una definizione che possa essere misurabile si utilizza la funzione logaritmo perché è l’unica che quando il suo argomento vale 1, il suo valore va a zero ed inoltre lo si caperà ancora di più quando si definisce l’entropia.

dove con si intende la probabilità con cui quel simbolo possa presentarsi.

Se la base del logaritmo è:

• 2 l’informazione si misura in bit
• 10 l’informazione si misura in hartley
• e (numero di Eulero) l’informazione si misura in nat

[:en]trasmesso e viene definita come la riduzione di incertezza che si poteva avere a priori sul simbolo trasmesso.
Sembra un panegirico ma, in realtà, il concetto è che se io trasmetto sempre un solo segnale sempre uguale, la probabilità di riceverlo è sempre 1. Ma tale fatto significa anche che l’informazione trasmessa è nulla.
Per trasmettere un’informazione vi è bisogno che si modifichi uno stato da luce a buio o viceversa; si pensi ai solo caratteri morse: per comunicare un messaggio, ossia un’informazione, si alternano i punti con le linee in un’opportuna combinazione.
Per dare una definizione che possa essere misurabile si utilizza la funzione logaritmo perché è l’unica che quando il suo argomento vale 1, il suo valore va a zero ed inoltre lo si caperà ancora di più quando si definisce l’entropia.

dove con si intende la probabilità con cui quel simbolo possa presentarsi.
Se la base del logaritmo è:
2 l’informazione si misura in bit
10 l’informazione si misura in hartley
e (numero di Eulero) l’informazione si misura in nat[:de]trasmesso e viene definita come la riduzione di incertezza che si poteva avere a priori sul simbolo trasmesso.
Sembra un panegirico ma, in realtà, il concetto è che se io trasmetto sempre un solo segnale sempre uguale, la probabilità di riceverlo è sempre 1. Ma tale fatto significa anche che l’informazione trasmessa è nulla.
Per trasmettere un’informazione vi è bisogno che si modifichi uno stato da luce a buio o viceversa; si pensi ai solo caratteri morse: per comunicare un messaggio, ossia un’informazione, si alternano i punti con le linee in un’opportuna combinazione.
Per dare una definizione che possa essere misurabile si utilizza la funzione logaritmo perché è l’unica che quando il suo argomento vale 1, il suo valore va a zero ed inoltre lo si caperà ancora di più quando si definisce l’entropia.

dove con si intende la probabilità con cui quel simbolo possa presentarsi.
Se la base del logaritmo è:
2 l’informazione si misura in bit
10 l’informazione si misura in hartley
e (numero di Eulero) l’informazione si misura in nat[:]

[:it]

1. Lanciando due monete qual è la probabilità di ottenere due teste?
2. Si lanciano due dadi. Trova la probabilità che escano due 3; che escano un 3 e un 4; che escano due numeri pari.
3. Calcola la probabilità che lanciando una moneta esca testa
4. Calcola la probabilità che lanciando 1 dado esca il numero 1.
5. Calcola la probabilità che lanciando 1 dado esca un numero divisibile per 2
6. Determina la probabilità che, lanciando 3 volte di seguito 1 moneta, si verifichi l’evento “esca almeno una croce”, sapendo che il primo lancio ha dato testa.
7. Da un’urna contenente 9 palline nere e 7 bianche si estraggono successivamente 3 palline, rimettendo ogni volta nell’urna la pallina estratta. Qual è la probabilità che siano tutte e tre nere? Che siano tutte e 3 bianche? Che siano le prime 2 bianche e la terza nera? Che siano  bianche e 1 nera?	;;;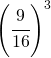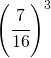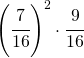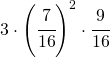

 [:]

[:it]

Samy Charnine

Dal post sulle probabilità condizionate si è affermato che:

che è uguale a scrivere:

ma nel caso in cui si abbiano eventi indipendenti

per cui si ha il principio delle probabilità composte ossia

Questa relazione è alla base della definizione di Entropia nell’ambito delle telecomunicazioni.

Esempio di applicabilità

Si vuole sapere qual è la probabilità che esca testa, nel lancio di una moneta due volte, sapendo che prima è uscita testa.

In questo caso si è in presenza di eventi indipendenti per cui la probabilità che esca testa al primo lancio è , la probabilità che esca nuovamente testa è , per cui la probabilità che in due lanci mi esca due volte testa vale .[:]

[:it]

Samy Charnine

Due eventi sono indipendenti se il verificarsi dell’uno non influisce sul calcolo della probabilità del verificarsi dell’altro

Due eventi sono dipendenti se il verificarsi dell’uno influisce sul calcolo della probabilità del verificarsi dell’altro.

Sono molto importanti queste due definizioni perché influiscono moltissimo nel caso in cui dovessi prevedere la trasmissione di un messaggio e quindi la necessità di trasmetterlo solo una volta o ritrasmetterlo.

Il primo esempio di eventi indipendenti potrebbe essere quello dell’estrazione di una pallina bianca da un’urna contente palline bianche e nere. In questo caso se dopo l’estrazione rimetto all’interno la pallina bianca estratta avrò eventi INDIPENDENTI ossia calcolare la probabilità di estrarre un’altra pallina bianca non dipende dall’estrazione precedente.

Se invece la pallina bianca non viene reintrodotta dall’urna allora tale fatto ha reso dipendente l’estrazione successiva da quella precedente.[:]

[:it]

Samy Charnine

E’ il caso in cui spesso si può trovare anche nell’ambito delle telecomunicazioni; se nella trasmissione di un fax , qual è la probabilità che essendo stato trasmesso un carattere bianco si possa avere un altro carattere bianco o un carattere nero?

In questo caso si è quindi nella situazione di probabilità subordinata o condizionata.

La probabilità che capiti l’evento A in seguito al fatto che si è verificato l’evento B è detta probabilità subordinata o probabilità condizionata e si indica con e si legge probabilità di A dato che si è verificato B.

Si può dimostrare facilmente che si calcola nella seguente maniera:

dove con si intende intersezione dei due eventi

in maniera analoga

.

Esempio:

E’ stata lanciata una moneta 3 volte ( o lanciate 3 monete in una volta sola). Qual è la probabilità che siano uscite tutte con la stessa faccia, sapendo che sono uscite meno di 2 teste?

La prima cosa che faccio è analizzare tutti i casi possibili del lancio di una moneta con i relativi risultati (esso si chiama spazio campionario o spazio degli eventi).

L’evento monete tutte con la stessa faccia A={}

L’evento monete su tre lanci almeno due teste B={}

[:]

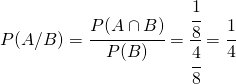[:it]

Yves Tanguy

• Due eventi sono incompatibili quando la loro probabilità non dipende dal fatto che accada o l’uno o l’altro.

Esempio: nell’estrazione di una carta da un mazzo di 40 carte, prendiamo in considerazione gli eventi:

1. : la carta estratta è un re;
2. : la carta estratta è un asso;
3. : la carta estratta è un re o un asso.

1. Essendoci quattro re su un mazzo di 40

2. Essendoci quattro assi su un mazzo di 40

3. In questo caso sommo semplicemente i due eventi

• Due eventi sono compatibili se essi sono possono capitare contemporaneamente.

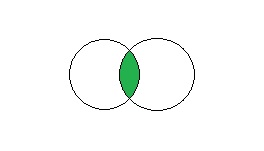
Esempio: nell’estrazione di una carta da un mazzo di 40 carte, prendiamo in considerazione gli eventi:

1. : la carta estratta è un re
2. : la carta estratta è una carta di cuori;
3. : la carta estratta è un re o una carta di cuori

1. Essendoci quattro re su un mazzo di 40

2.Ci sono 10 carte di cuori per cui

3. Nel terzo caso i casi favorevoli sono costituiti da 10 carte di cuori sommando i quattro re a cui devo sottrarre il caso in cui entrambi gli eventi possano capitare

In pratica si è in questa situazione in cui si deve sottrarre la contemporaneità degli eventi che altrimenti si conterebbero due volte:

in quanto ho sottratto la probabilità che l’evento sia una carta di cuori e che sia proprio un re.[:]

[:it]

Joan Miró

Credere di esaurire la teoria della probabilità in pochi post è un’impresa molto ardua, per cui esso si pone solo come punto di sviluppo per una trattazione più approfondita attraverso lezioni di approfondimento in aula o su libri strettamente specifici.

Il concetto di fenomeno aleatorio si contrappone a quello di fenomeno deterministico. Ad esempio il moto di un corpo sottoposto alla forza di gravità terrestre; le leggi della dinamica e della cinematica consentono di determinarne in modo esatto la traiettoria, note che siano le condizioni iniziali e il valore dell’accelerazione di gravità.

Note cioè le cause, si possono esattamente valutare gli effetti e il fenomeno si può considerare deterministico.

Da un’analisi più accurata si nota che le condizioni iniziali e l’accelerazione di gravità non sono mi esattamente note per le inevitabili  incertezze di misura, la stessa traiettoria può essere osservata soltanto entro certi limiti d’approssimazione.

In queste circostanze la traiettoria del corpo non è esattamente prevedibile e il modello deterministico precedentemente  considerato può fornire soltanto indicazioni di massima su quello che sarà la traiettoria osservata.

Può accadere tuttavia che un’analisi più accurata dei risultati riveli una sorta di REGOLARITA’ STATISTICA nel senso che la traiettoria “media” da definirsi in maniera opportuna, tende sempre più a stabilizzarsi con l’aumentare del numero di osservazioni.

Quest’ultima frase è alla base delle telecomunicazioni nel senso che un segnale trasmesso non si ha mai la certezza di come esso possa arrivare al destinatario ma si può descrivere in maniera statistico come esso possa arrivare al destinatario stesso e sapendo la funzione statistica che lo descrive si può prevedere come esso possa essere ricevuto.

Andrej Nikolaevič Kolmogorov

ASSIOMI DI KOLMOGROV

1- Ad ogni evento casuale a corrisponde un certo numero P(a), chiamato “probabilità di a“, che soddisfa la disuguaglianza .

2- La probabilità dell’evento certo è 1

3- La probabilità dell’unione di un numero finito o infinito numerabile di eventi mutuamente esclusivi è pari alla somma delle probabilità di questi eventi

La prima definizione porta quindi a definire la

dove m sono i casi favorevoli, ed n  i casi possibili.[:]