[:it]Per verificare che pacchetti sono installati sul sistema è sufficiente digitare il comando
cat /var/lib/dpkg/status
ad esempio per verificare se Python è installato o meno si digiti:
Con il comando:
dpkg -l
ho la lista completa dei pacchetti installati.
mentre con il comando
dpkg -l>elenco.txt
salvo l’intero elenco in un file chiamato elenco.txt[:]
[:it]
giacomo balla
Un campo magnetico variabile comporta l’esistenza di un campo elettrico e viceversa che un campo elettrico variabile comporta l’esistenza di un campo magnetico, e questo è una conseguenza del principio di relatività.
Le equazioni di Maxwell (alla base dell’elettromagnetismo) sono invarianti per le trasformazioni di Lorentz (sistema di riferimento relativistico), mentre non lo sono per quelle di Galileo.
Nel post che mette in relazione il potenziale elettrico con il campo elettrico, si era arrivati ad affermare che:
ossia:
inoltre il flusso di campo magnetico è dato da:
adesso unendo queste nella formula di Farady:
si ha:
In forma differenziale e lo inserisco solo per coerenza nella trattazione specifica la relazione precedente può essere scritta come:
che si legge il rotore di E è dato dalla variazione nel tempo del campo induzione magnetico.[:]
[:it]
Giacomo Balla
Uno dei fenomeni elettromagnetici familiari allo studente è l’indizione elettromagnetica che fu scoperta simultaneamente ed indipendentemente da Michael Farady (1791-1867) e Joseph Henry (1797-1878).
L’induzione elettromagnetica è il principio di funzionamento del generatore elettrico, del trasformatore, della dinamo della bicicletta e molti altri apparecchi di uso quotidiano.
Ecco il fenomeno:
si abbia un conduttore elettrico formante un circuito chiuso e posto in una regione nella quale esista un campo magnetico. Se il flusso magnetico varia con il tempo, si può osservare una corrente nel circuito mentre il flusso sta variando. La presenza di una corrente elettrica indica l’esistenza, o l’induzione, di una fem agente nel circuito.
Tale affermazione di razionalizza attraverso la seguente formula:
.
In un campo magnetico variabile, in ogni circuito viene indotta una fem uguale alla derivata rispetto al tempo del flusso magnetico attraverso il circuito col segno cambiato.[:]
[:it]
Wilhem E. Weber
Il flusso magnetico attraverso un qualsiasi superficie, chiusa o no, è:
il concetto di flusso magnetico attraverso una superficie arbitraria è di grande importanza, specialmente quando la superficie non è chiusa.
Il flusso magnetico, che il campo induzione magnetico per un’area è espressa in ![\left [ Tm^{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c4652015f2ec3bf36d90651f2baea70a_l3.png "Rendered by QuickLaTeX.com")
(Tesla metro al quadrato) e viene chiamato weber (wb) in onore del fisico tedesco Wilhem E. Weber (1804-1891).
Poiché non esistono masse o poli magnetici, le linee di forza del campo induzione magnetica sono chiuse, come si dimostra sperimentalmente.
il flusso del campo magnetico attraverso una superficie chiusa è sempre nullo
Cioè il flusso entrante attraverso una superficie chiusa è uguale al flusso uscente. in forma analitica si ha:
Il risultato costituisce la legge di Gauss per il campo induzione magnetica.
In forma differenziale, con gli stessi passaggi usati per il campo elettrico (prima equazione di Maxwell) la sua forma differenziale diventa:
in forma differenziale diventa:
Ossia la divergenza del campo indizione magnetica è nulla.
Essa prende il nome di II equazione di Maxwell.[:]
[:it]
Giacomo Balla
creare una pagina mettendo la scritta: questa è la prima pagina web ad una distanza 700 a sinistra e 500 rispetto all’alto.
Il corpo del documento racchiude le informazioni che riguardano il contenuto del documento html.
Gli attributi del tag <body> possono essere sostituiti integralmente facendo uso dei fogli di stile.
Il tag <body> possiede una serie di attributi: eccone i principali.
I margini
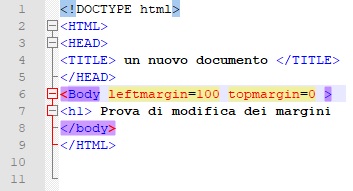
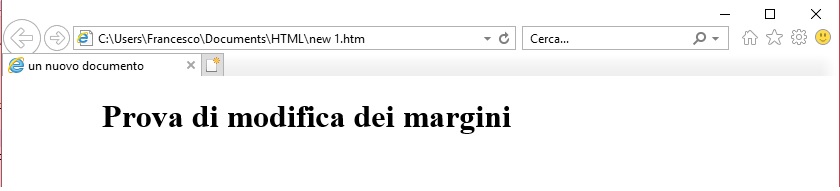
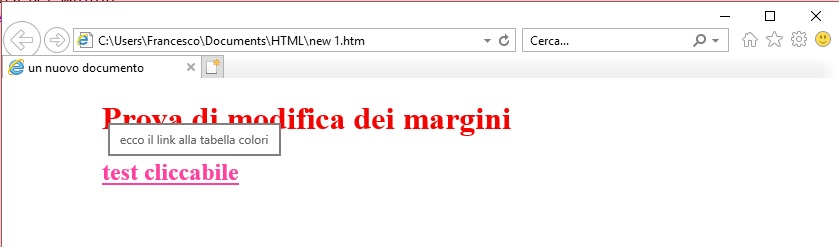
La proprietà margin consente di ridefinire i margini del documento: per margini si intende la distanza del testo dal bordo della finestra de browser: leftmargin per modificare il margine sinistro e topmargin per modificare il margine superiore.
Eccone un esempio come codice e come effetto:
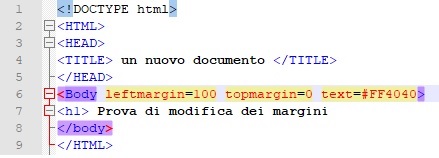
Il colore del testo
La proprietà per il colore del testo è text, eccone un esempio di suo utilizzo
Ecco il link alla tabella colori
Il colore dei collegamenti ipertestuali
La proprietà ha il nome di link. Il colore dei collegamenti visitati può essere modificato con la proprietà vlink, analogamente a quanto visto per il colore dei link ipertestuali. Solitamente è di colore viola.
Eccone un esempio del suo utilizzo
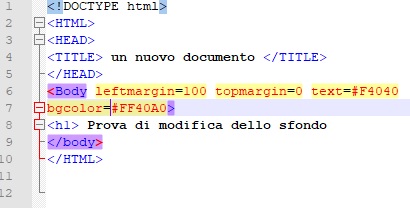
Il colore di sfondo (background)
La proprietà ha il nome di bgcolor. La sintassi è bgcolor=”colore”.
Le immagini di sfondo
La proprietà ha nome background. Lo sfondo possiede una funzione chiamata “texture” che replica più volte la stessa immagine per riempire tutto lo spazio disponibile. Per ottenere un effetto di continuità è necessario usare immagini di ridotte dimensioni.
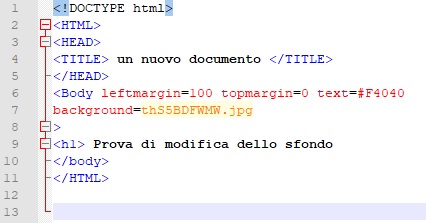
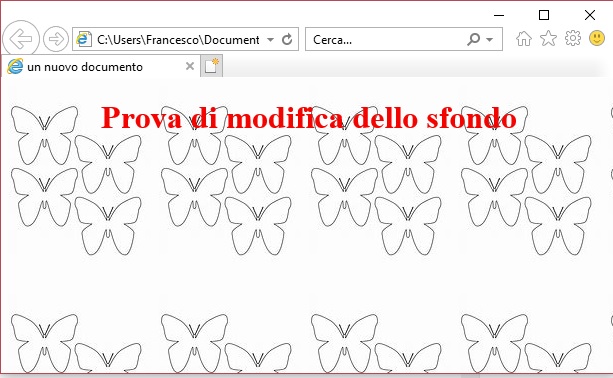
In questo caso l’immagine è presente nella stessa directory in cui è posizionata l’immagine
questo è l’effetto:
[:it]
Giacomo Balla
il problema del calcolo del Massimo Comune Divisore utilizza l’algoritmo di Euclide. Prevede la divisione dei due numeri m ed n: se la divisione ha resto 0 (zero) , il secondo numero è il divisore, altrimenti si ripete la divisione tra n ed il reto r della divisione. Creare il programma.
[:]
[:it]Questo programma implementa il fattoriale in maniera ricorsiva. La ricorsione utilizza lo stack in memoria per mantenere l’informazione della prima chiamata alla funzione finchè non arriva alla condizione di uscita, a questo punto libera lo stack un gradino alla volta a ritroso.
[:]
[:it]Questo programma implementa il fattoriale in maniera ricorsiva. La ricorsione utilizza lo stack in memoria per mantenere l’informazione della prima chiamata alla funzione finchè non arriva alla condizione di uscita, a questo punto libera lo stack un gradino alla volta a ritroso.
[:]
[:it]
Stack o pila
La funzione che implementa il calcolo del fattoriale di un numero è un esempio di calcolo ricorsivo.
funzione fattoriale(intero n)
se n=0
ritorna il valore 1
altrimenti
n=n*fattoriale(n)
In pratica l’elaboratore mette in parcheggio il valore della variabile n finchè essa non ritorna il valore 1. La memoria dell’elaboratore crea delle aree di memoria che assumono il valore precedente come una pila.
Prima riempie la pila e poi la svuota terminando. Ossia nel primo gradino mette il valore più elevato poi, man mano che aumenta inserisce il valore meno elevato.
La ricorsione ha un vantaggio fondamentale: permette di scrivere poche linee di codice per risolvere un problema anche molto complesso. Tuttavia, essa ha anche un enorme svantaggio: le prestazioni.
Infatti, la ricorsione genera una quantità enorme di overhead, occupando lo stack per un numero di istanze pari alle chiamate della funzione che è necessario effettuare per risolvere il problema. Funzioni che occupano una grossa quantità di spazio in memoria, pur potendo essere implementate ricorsivamente, potrebbero dare problemi a tempo di esecuzione. Inoltre, la ricorsione impegna comunque il processore in maniera maggiore per popolare e distruggere gli stack.
[:]