[:it]

max ernst
Lavorare con i file è il primo passo verso la programmazione batch. Tale termine è utilizzato per tutti quei processi che vengono eseguiti in background ossia senza accorgersi dal computer.
Ad esempio l’analisi della presenza di virus è un tipico processo batch, un altro potrebbe essere quello della deframmentazione dei dischi.
Un file può essere aperto per essere letto o per essere scritto; tale distinzione permette al sistema operativo di essere più veloce in quanto tale due processi presuppongono operazioni diverse.
Ecco i primi comandi per la gestione dei file:
miofile = open(‘pippo.txt’,’w’)
miofile.write(‘ciao sono francescon’)
miofile.close()
# mi dice come ho aperto il mio file ed il relativo nome
print miofile
miofile = open(‘pippo.txt’,’r’)
print miofile.read()
miofile.close()
Ecco un altro esempio molto più complesso ma ricco di spunti per la gestione di un file:
import string
true = 1
false = 0
def print_numbers(numbers):
print "Telephone Numbers:"
for x in numbers.keys():
print "Name: ",x," \tNumber: ",numbers[x]
print
def add_number(numbers,name,number):
numbers[name] = number
def lookup_number(numbers,name):
if numbers.has_key(name):
return "The number is "+numbers[name]
else:
return name+" was not found"
def remove_number(numbers,name):
if numbers.has_key(name):
del numbers[name]
else:
print name," was not found"
def load_numbers(numbers,filename):
in_file = open(filename,"r")
while true:
in_line = in_file.readline()
if in_line == "":
break
in_line = in_line[:-1]
[name,number] = string.split(in_line,",")
numbers[name] = number
in_file.close()
def save_numbers(numbers,filename):
out_file = open(filename,"w")
for x in numbers.keys():
out_file.write(x+","+numbers[x]+"\n")
out_file.close()
def print_menu():
print '1. Print Phone Numbers'
print '2. Add a Phone Number'
print '3. Remove a Phone Number'
print '4. Lookup a Phone Number'
print '5. Load numbers'
print '6. Save numbers'
print '7. Quit'
print
phone_list = {}
menu_choice = 0
print_menu()
while menu_choice != 7:
menu_choice = input("Type in a number (1-7):")
if menu_choice == 1:
print_numbers(phone_list)
elif menu_choice == 2:
print "Add Name and Number"
name = raw_input("Name:")
phone = raw_input("Number:")
add_number(phone_list,name,phone)
elif menu_choice == 3:
print "Remove Name and Number"
name = raw_input("Name:")
remove_number(phone_list,name)
elif menu_choice == 4:
print "Lookup Number"
name = raw_input("Name:")
print lookup_number(phone_list,name)
elif menu_choice == 5:
filename = raw_input("Filename to load:")
load_numbers(phone_list,filename)
elif menu_choice == 6:
filename = raw_input("Filename to save:")
save_numbers(phone_list,filename)
elif menu_choice == 7:
pass
else:
print_menu()
print "Goodbye"
[:en]

Salvador Dalì
Lavorare con i file è il primo passo verso la programmazione batch. Tale termine è utilizzato per tutti quei processi che vengono eseguiti in background ossia senza accorgersi dal computer.
Ad esempio l’analisi della presenza di virus è un tipico processo batch, un altro potrebbe essere quello della deframmentazione dei dischi.
Un file può essere aperto per essere letto o per essere scritto; tale distinzione permette al sistema operativo di essere più veloce in quanto tale due processi presuppongono operazioni diverse.
Ecco i primi comandi per la gestione dei file:
miofile = open(‘pippo.txt’,’w’)
miofile.write(‘ciao sono francescon’)
miofile.close()
# mi dice come ho aperto il mio file ed il relativo nome
print miofile
miofile = open(‘pippo.txt’,’r’)
print miofile.read()
miofile.close()[:de]

Salvador Dalì
Lavorare con i file è il primo passo verso la programmazione batch. Tale termine è utilizzato per tutti quei processi che vengono eseguiti in background ossia senza accorgersi dal computer.
Ad esempio l’analisi della presenza di virus è un tipico processo batch, un altro potrebbe essere quello della deframmentazione dei dischi.
Un file può essere aperto per essere letto o per essere scritto; tale distinzione permette al sistema operativo di essere più veloce in quanto tale due processi presuppongono operazioni diverse.
Ecco i primi comandi per la gestione dei file:
miofile = open(‘pippo.txt’,’w’)
miofile.write(‘ciao sono francescon’)
miofile.close()
# mi dice come ho aperto il mio file ed il relativo nome
print miofile
miofile = open(‘pippo.txt’,’r’)
print miofile.read()
miofile.close()[:]
 Una volta che si riesce a calcolare la derivata prima di una funzione si può cominciare ad intuire come potrà essere il suo grafico. In particolare siccome la derivata prima fornisce il valore dell’inclinazione della curva tangente si può capire che quando essa si annulla la relativa retta è orizzontale.
Una volta che si riesce a calcolare la derivata prima di una funzione si può cominciare ad intuire come potrà essere il suo grafico. In particolare siccome la derivata prima fornisce il valore dell’inclinazione della curva tangente si può capire che quando essa si annulla la relativa retta è orizzontale.![]() .
.![]()
![]()
![]()
![]()
![]()
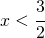
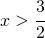
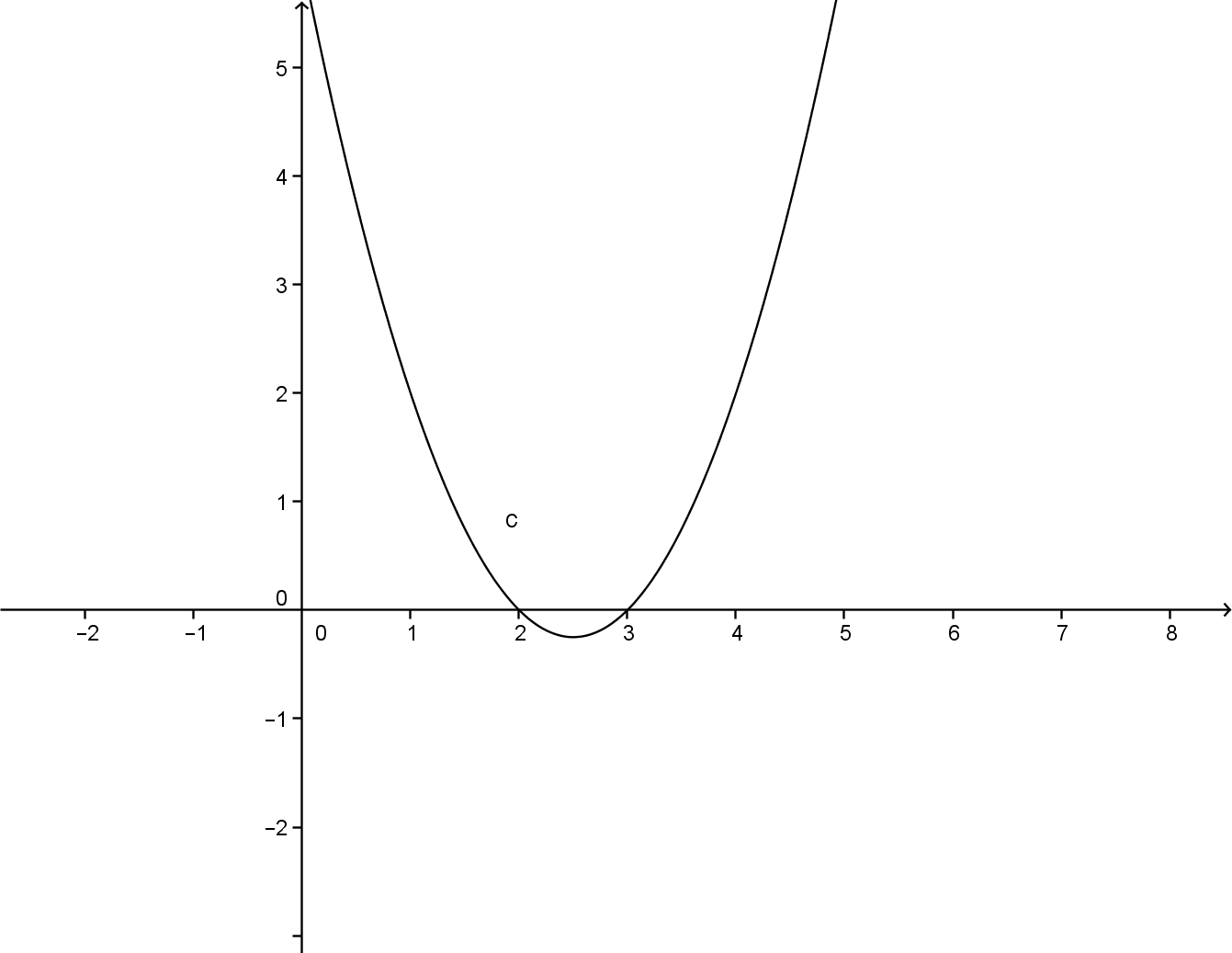
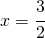 è il punto di minimo (in questo caso anche assoluto della funzione).
è il punto di minimo (in questo caso anche assoluto della funzione).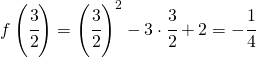
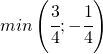

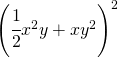 .
.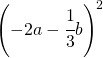 .
.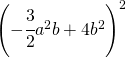 .
.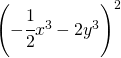 .
.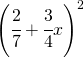 .
.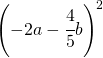 .
.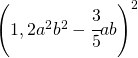 .
.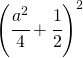 .
. .
.

![Rendered by QuickLaTeX.com \left [y^{'}=-\cfrac{1}{x^2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-95d7e93f5fef6dffb7a19e2f44222eca_l3.png)
 .
.