[:it]Si consideri una carica puntiforme ![]() e si calcoli il flusso del campo elettrico
e si calcoli il flusso del campo elettrico ![]() da essa prodotta attraverso una superficie sferica avente il centro coincidente con la carica.
da essa prodotta attraverso una superficie sferica avente il centro coincidente con la carica.
Il flusso, in generale, è il calcolo della quantità che attraversa una superficie chiusa.

Si divide la superficie in superfici molto piccole (o infinitesime) di aree ![]() ,
, ![]() ,
, ![]() ,…Su ciascuna di esse si può disegnare un vettore unitario
,…Su ciascuna di esse si può disegnare un vettore unitario ![]() ,
, ![]() ,
,![]() ,…perpendicolare alla superficie in quel punto.
,…perpendicolare alla superficie in quel punto.
Siano ![]() ,
, ![]() ,
, ![]() ,… (theta) gli angoli tra i vettori normali
,… (theta) gli angoli tra i vettori normali ![]() ,
, ![]() ,
,![]() ,…e i vettori del campo
,…e i vettori del campo ![]() ,
, ![]() ,
, ![]() ,… in ogni punto della superficie.
,… in ogni punto della superficie.
Allora il flusso ![]() del campo vettoriale
del campo vettoriale ![]() attraverso la superficie S è:
attraverso la superficie S è:
![]()
sapendo che ![]()
il flusso può essere scritto come:
![]()
ma sapendo cheil prodotto di una base per un’altezza mi fornisce proprio un integrale la realazione precedente può essere scritta come:
![]()
dove il segno di circoletto sull’integrale significa che è superficie chiusa.
Tutta questa premessa è servita per applicarla al campo elettrico.
Si calcola il flusso del campo elettrico attraverso una superficie sferica.
![]()
Il vettore unitario normale ad una sfera coincide con il vettore unitario ![]() lungo la direzione radiale .
lungo la direzione radiale .
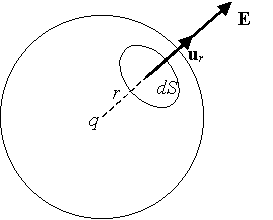
Perciò l’angolo ![]() fra il campo elettrico e il vettore unitario normale è nullo e
fra il campo elettrico e il vettore unitario normale è nullo e ![]() .
.
Il campo elettrico ha lo stesso valore in tutti i punti della superficie sferica e che l’area della sfera è ![]() .
.
Il valore del flusso del campo elettrico risulta:
![]()
concludendo
![]()
La legge di Gauss è particolarmente utile quando si vuole calcolare il campo elettrico prodotto da distribuzioni di carica aventi determinate simmetrie geometriche ad esempio piastre, sfere, o fili percorsi da corrente.[:]
