[:it]
Guido Borelli
Una sfera, il cui centro è il punto 
è tangente al piano 
di equazione 
. Qual è il punto di tangenza? Qual è il raggio della sfera?
Sviluppo
Il primo passo è determinare il raggio della sfera attraverso la determinazione della distanza tra il centro ed il piano:
dove con 
sono le tre coordinate del centro, e a,b,c,d sono i rispettivi coefficienti numerici di 
ed il termine noto.
La relazione precedente diventa quindi:
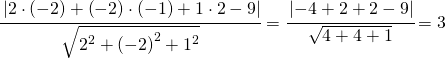
L’equazione della sfera generica è:
Sostituendo i valori numerici diventa:
metto a sistema l’equazione della sfera con quella del piano ed ho il punto di tangenza:
se continuassi tale metodo mi troverei però un’equazione in due incognite infatti avrò:
Il metodo risolutivo è allora il seguente.
I coefficienti numerici del piano rappresentano le coordinate del vettore perpendicolare al piano, ed il centro rappresenta proprio un punto che appartiene alla retta cercata che avrà equazione parametrica:
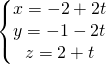
adesso si sostituiscono i valori nell’equazione del piano determinando t:
Adesso si sostituisce il valore trovato nell’equazione parametrica del piano e si trova il punto d’intersezione.
x=0
y=-3
z=3
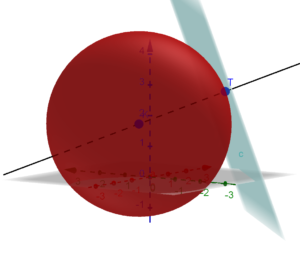
Graficamente si ha la seguente situazione:
[:]