
Igor Morski
Quale metodo usare per risolvere i sistemi d’equazione nel minor tempo possibile e in maniera corretta?
- se ho già la x o la y espressa in funzione dell’altra conviene usare il metodo della sostituzione
- se ho nelle due equazioni la x o la y con segno opposto conviene usare il metodo dell’addizione.
- se ho già espresso la x o la y in funzione dell’altra variabile conviene usare il metodo del confronto.
- in tutti i casi il metodo di Cramer è il più meccanico e veloce ma bisogna impostarlo bene e non sbagliare il determinante della radice.
Qui inserisco una serie di esercizi e nelle soluzioni inserisco il metodo che io ritengo migliore ma non necessariamente quello che tutti possono ritenere migliore. Alla fine uno può trovarsi meglio aver usato un metodo invece che un altro.
Esercizi facili per prendere la mano (6)
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
![Rendered by QuickLaTeX.com \left [ \left ( 1,\cfrac{3}{2} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-bc1069d7f684e3b18c1030db0db3c4be_l3.png) |
| 6.7. |
Esercizi più complessi (7)
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
7.4. 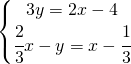 |
![Rendered by QuickLaTeX.com \left [ \left ( \cfrac{5}{3},-\cfrac{2}{9} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-97bb486ade1c64964c37a04a3fde6c30_l3.png) |
7.5. 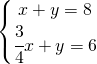 |
|
7.6. 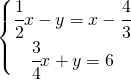 |
Verso un buon livello (8)
8.1. 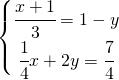 |
|
Verso il l’ottimo (9)
9.1. 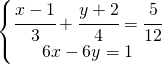 |
![Rendered by QuickLaTeX.com \left [ \left (\cfrac{1}{2},\cfrac{1}{3} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-801c5aa12d2b23cdf869d61901284917_l3.png) |
L’ottimo (10)
10.1. 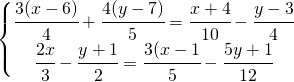 |
|

il 7.2 e il 7.3 sono uguali, ma con 2 risultati diversi