Una retta sul piano può essere parallela all’asse delle ascisse (orizzontale), parallela all’asse delle ordinate (verticale) e quindi, conseguentemente anche obliqua.
In maniera analoga un asintoto può essere verticale, orizzontale ed obliquo.
Per la presenza di un asintoto obliquo DEVONO essere vere le seguenti due condizioni basta che una delle due non sia soddisfatta che l’asintoto non sia presente:
(1) ![]()
che mi fornisce il coefficiente angolare della “retta” asintoto
(2) ![]()
Ribadisco il fatto che è sufficiente che una delle due non sia vera ossia che mi dia un limite non finito affinché non vi sia il limite obliquo.
Ecco immediatamente un esempio:
sia ![]()
allora applico la (1)
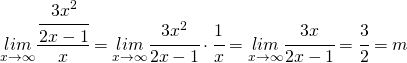
adesso applico la (2) per trovare la ![]()
![Rendered by QuickLaTeX.com \underset{x\rightarrow\infty}{lim}\left[\cfrac{3x^{2}}{2x-1}-\cfrac{3}{2}x\right]=\underset{x\rightarrow\infty}{lim}\cfrac{6x^{2}-3x(2x-1)}{(2x-1)\cdot2}=\underset{x\rightarrow\infty}{lim}\cfrac{6x^{2}-6x^{2}+3x}{(2x-1)\cdot2}=\underset{x\rightarrow\infty}{lim}\cfrac{3x}{4x-2}=\cfrac{3}{4}=q](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8c7607f686ead3f6506f65e7541a9133_l3.png)
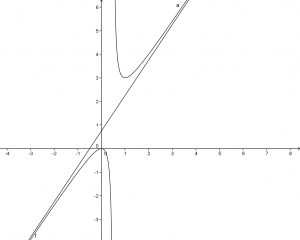
l’asintoto è:
![]()
Il grafico risulta: