[:it]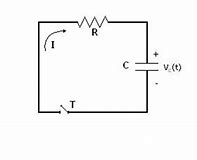
Collegando un condensatore di capacità C, inizialmente scarico, attraverso una resistenza R ai poli di una batteria (corrente continua) di f.e.m f, la carica q sulle armature, tende a raggiungere il valore nominale fC.
Tenendo conto che tra le armature del condensatore c’è una caduta i tensione q/C, si ha:
sapendo che:
si deve risolvere la seguente equazione differenziale:
è un’equazione differenziale lineare completa che si può risolvere mediante il metodo di Lagrange ossia data:
essa ha soluzione generica:
![y=e^{-\int a(x)dx}\cdot\left [ \int b(x)e^{\int a(x))dx}+c \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-db42e35177ee1f408e5eb7c1d24c2996_l3.png "Rendered by QuickLaTeX.com")
applicandola alle variabili in gioco si ha:
dove 
e 
applicando la soluzione generica si ha:
![q=e^{-\int \frac{1}{RC}dt}\cdot \left [ \int \frac{f}{R}e^{\int \frac{1}{RC}dt}+c \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8d3f5e5d4c5af1f7af741e6c377c34eb_l3.png "Rendered by QuickLaTeX.com")
![q=e^{-\frac{1}{RC}t}\cdot \left [ \int \frac{f}{R}e^{\frac{1}{RC}t}+c \right ]=e^{-\frac{1}{RC}t}\cdot\left [ \frac{f}{R}\cdot RC e^{\frac{1}{RC}t}+c \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-34c00c8370f4942494f94332cdfa4dbb_l3.png "Rendered by QuickLaTeX.com")
sapendo che all’inizio, ossia al tempo t, il condensatore è scarico allora q(0)=0 e sostituendo tale condizione all’equazione trovata si ha:
in definitiva:
(1)
e si indica con 
la costante di tempo.
sapendo che 
la d.d.p. tra le armature del condensatore è perciò:
La corrente
per cui derivando la (1) si ha:
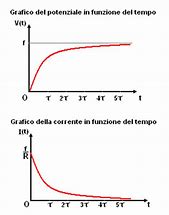
La rappresentazione grafica è la seguente:
[:]