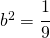[:it]
Jim Warren
Ricapitolando.
Un’ellisse è caratterizzata dai sui vertici, dalle coordinate dei fuochi, dall’eccentricità.
Per poterla disegnare si annulla prima la x e si trovano le intersezioni con l’asse y e viceversa.
Rappresentare graficamente le seguenti ellissi, dopo aver determinato, di ciascuna di esse, le coordinate dei vertici, quelle dei fuochi e l’eccentricità.
Esercizi per un livello sufficiente (6):
6.1.  \ |
|
6.2.  |
|
6.3.  |
|
6.4.  |
|
| 6.5. Determina la misura degli assi dell’ellisse:
|
![\left [ 12;6 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-b9a3ae57c7f46367e69a09551f22e267_l3.png "Rendered by QuickLaTeX.com") |
6.6.Determina le coordinate dei fuochi dell’ellisse:  |
![\left [ \left ( \pm \sqrt{21},0 \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-31a40c2d215dd51362c8c714ea1d98fd_l3.png "Rendered by QuickLaTeX.com") |
Esercizi per un livello discreto (7):
7.1.  |
|
7.2.  |
|
7.3.  |
|
| 7.4. Determina la misura degli assi dell’ellisse:
|
![\left [ \cfrac{4}{\sqrt{3}};12 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5c87560651d92e6ddc58fae10715b0d4_l3.png "Rendered by QuickLaTeX.com") |
7.5. Determina le cocordinate dei fuochi:  |
![\left [ \left ( 0;\pm \sqrt{21} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8d176bf5e7a138a69955fe7ccde35509_l3.png "Rendered by QuickLaTeX.com") |
Esercizi per un buon livello (8)
8.1.  |
8.2.  |
8.3.  |
9.1. Determina l’equazione del luogo geometrico dei punti tali che la somma delle distanze dai punti  e  è uguale a 20. |
![\left [\cfrac{x^2}{100}+\cfrac{y^2}{64}=1 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-db4a27f5148afa23d64f35bf50b1869e_l3.png "Rendered by QuickLaTeX.com") |
9.2. Determina l’equazione del luogo geometrico dei punti tali che la somma delle distanze dai punti  e  è uguale a 20. |
![\left [\cfrac{x^2}{36}+\cfrac{y^2}{100}=1 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-4394ec2c524d27801983334d705a5b57_l3.png "Rendered by QuickLaTeX.com") |
soluzioni[:en]
Jim Warren
Ricapitolando.
Un’ellisse è caratterizzata dai sui vertici, dalle coordinate dei fuochi, dall’eccentricità.
Per poterla disegnare si annulla prima la x e si trovano le intersezioni con l’asse y e viceversa.
Rappresentare graficamente le seguenti ellissi, dopo aver determinato, di ciascuna di esse, le coordinate dei vertici, quelle dei fuochi e l’eccentricità.
Esercizi per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
Esercizi per un livello discreto (7):
| 7.1. |
| 7.2. |
| 7.3. |
Esercizi per un buon livello (8)
| 8.1. |
| 8.2. |
| 8.3. |
[:de]
Jim Warren
Ricapitolando.
Un’ellisse è caratterizzata dai sui vertici, dalle coordinate dei fuochi, dall’eccentricità.
Per poterla disegnare si annulla prima la x e si trovano le intersezioni con l’asse y e viceversa.
Rappresentare graficamente le seguenti ellissi, dopo aver determinato, di ciascuna di esse, le coordinate dei vertici, quelle dei fuochi e l’eccentricità.
Esercizi per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
Esercizi per un livello discreto (7):
| 7.1. |
| 7.2. |
| 7.3. |
Esercizi per un buon livello (8)
| 8.1. |
| 8.2. |
| 8.3. |
[:]
Salve Professore, non riesco a svolgere gli esercizio 7.3, ho provato varie soluzioni, ma non riesco a capire quale sia. Pur semplificando non riesco ad ottenere l’equazione dell’ellisse. Come devo fare?
Scrivere
è come scrivere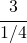 
per cui applicando la stessa l’ellisse 
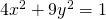diventa 
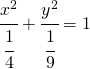per cui 
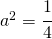e 