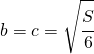Tra tutti i parallelepipedi rettangoli a base quadrata, con superficie totale di area S, determinare quello per cui la somma delle lunghezze degli spigoli è minima.
Prerequisiti
- saper sviluppare i problemi di massimo e minimo
- nozione di base della geometria dei solidi per il calcolo della superficie totale
- saper calcolare la derivata prima e la relativa disequazione
Sviluppo
Considero 
la dimensione della base del mio parallelepipedo, devo esprimere la terza dimensione, che chiamerò 
per comodità in funzione di x e dell’altro termine che conosco ossia la superficie totale.
Tutto questo per trovare il 
ma 
per cui risulta:
La superfice totale risulta:
risolvendola tenendo come incognita :
La funzione di cui dovrò calcolare il minimo sarà perciò:
facendone la derivata prima si ha:
annullando il numeratore di vede che le soluzioni sono:
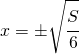
ed è positiva per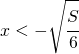 
ed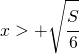 
quindi il punto di minimo è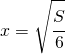 
da cui si ricavano le tre dimensioni:
