[:it]La funzione distribuzione di probabilità viene utilizzata per descrivere un fenomeno aleatorio (casuale) e fornire la probabilità che un certo evento accada o meno.
In particolare essa segue gli assiomi di Kolmogrov generalizzandoli.
La funzione distribuzione viene così definita:
![F_{x}(a)=P\left [ x\leqslant a \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-133aaf4e7a715a30fa15bc545d258d8e_l3.png "Rendered by QuickLaTeX.com")
conseguenza immediata è che:
![P\left [ a \leqslant x\leqslant b \right ]=F_{x}(b)-F_{x}(a)](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-1695d4a5d6953e0e0b09a26ace9af8f0_l3.png "Rendered by QuickLaTeX.com")
che ricorda moltissimo il teorema del calcolo integrale ed il teorema di Torricelli-Barrow
Infatti si definisce la funzione densità di probabilità:
che comporta la seguente affermazione:
![P\left [ a \leqslant x\leqslant b \right ]=F_{x}(b)-F_{x}(a)=\int_{a}^{b}f_{x}(c)dc](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-0cf3227cfce2e1f930bb0d57876fe636_l3.png "Rendered by QuickLaTeX.com")
ossia la funzione densità di probabilità è la derivata della funzione distribuzione di probabilità o detto alla stessa maniera, la funzione distribuzione è l’integrale della funzione densità in un determinato intervallo.
Per chiarire immediatamente il concetto la funzione densità di probabilità più usata e conosciuta è la distribuzione di Gauss che descrive fenomeni aleatori continui che si concentrano verso un valore più probabile centrale.
La sua equazione è:
la forma della campana e il suo valore centrale dipendono dalla deviazione standard 
e dalla media 
.
Eccone un suo grafico:
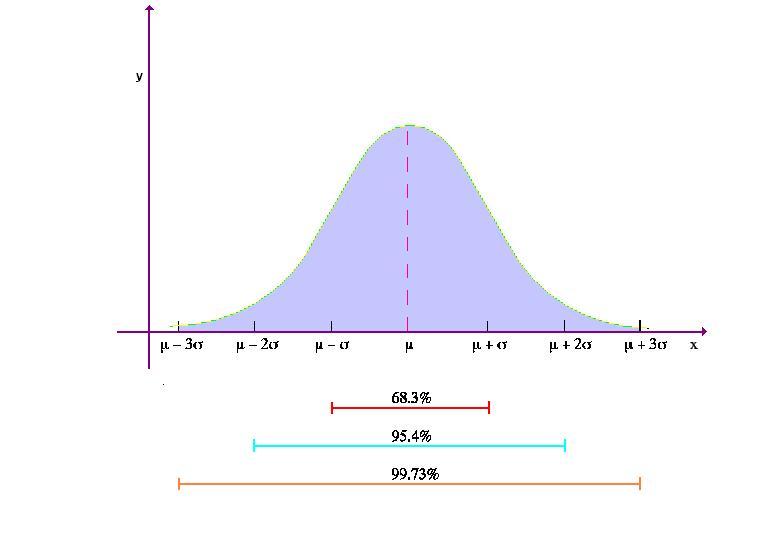
Per capire la probabilità che una misura cada in un certo intervallo si deve calcolare l’area sottesa dalla curva in quell’intervallo ossia la sua funzione distribuzione o funzione primitiva negli intervalli presi in esame.[:]
Prof anche leggendo il post faccio ancora fatica a capire cosa sia effettivamente la densità di probabilità.