[:it]Geometria nello spazio: esercizio 3[:]

Pubblicato il 13 Maggio 2017 da admin

[:it]

Paul Klee

Data la retta di equazione:

$\left\{\begin{matrix} x=t\\ y=2t\\ z=t \end{matrix}\right.$

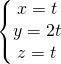
e la retta di equazione:

$\left\{\begin{matrix} x+y+z-3=0\\ 2x-y=0 \end{matrix}\right.$

ed il punto $P(1,0,-2)$

determinare l’equazione del piano passante per P e parallelo alle due rette.

Svolgimento

Perché esista tale piano le due rette devono essere complanari ed affinché che tale condizione sia soddisfatta è necessario che si intersechino in un punto.

E’ sufficiente determinare il valore di t sostituendo le coordinate nella seconda retta:

$\left\{\begin{matrix} t+2t+t-3=0\\ 2t-2ty=0 \end{matrix}\right.$

$t=\cfrac{3}{4}$

ed il punto di intersezione esiste e vale:

$T\left ( \cfrac{3}{4},\cfrac{3}{2},\cfrac{3}{4} \right )$

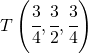
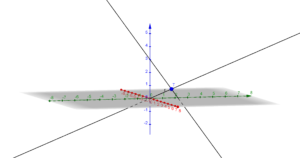
Adesso trovando il piano che contiene le due rette posso determinare poi quello parallelo passante per il punto P.

Per determinare il piano che contiene le due rette è sufficiente prendere due punti di una retta ed un terzo dell’altra e trovare il piano passante per questi tre punti.

$A(0,0,0)$ con $t=0$ e $B(1,2,1)$ con $t=1$ appartengono alla prima retta mentre $C(0,0,3)$ appartiene alla seconda retta.

Adesso sostituendo questi punti all’equazione generica del piano cartesiano

$ax+by+cz+d=0$

devo

$\left\{\begin{matrix} d=0\\ a+2b+c=0\\ 3c+d=0 \end{matrix}\right.$

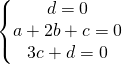
che risolto dà:

$\left\{\begin{matrix} d=0\\ c=0\\ a=-2b \end{matrix}\right.$

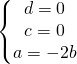
L’equazione del piano diventa:

$-2bx+by=0$

divido per b

$-2x+y=0$

Adesso trovo il piano passante per il punto P

$a-2c+d=0$

e pongo la condizione che deve esser parallelo a quello appena trovato ossia

$-\cfrac{2}{a}=\cfrac{1}{b}=\cfrac{0}{c}$

$-2b=a$

$c=0$

$d=2b$

e l’equazione del piano passante per P e parallelo alle due rette ha equazione:

$-2x+y+2=0$

[:]

Questa voce è stata pubblicata in Senza categoria. Contrassegna il permalink.

Lascia un commento Annulla risposta