[:it]

Norman Rockwell
Per trovare la soluzione in questo caso, invece che trovare il punto medio, come nel metodo di bisezione, si trova la retta passante per i due punti, per cui vale il teorema di unicità della radice, e si determina il suo punto di intersezione con l’asse delle x.
L’errore o approssimazione è data dalla differenza tra le due intersezioni successive ossia:
![]()
La retta passante per i due estremi ha equazione:
![]()
e la sua intersezione vale:
![]()
Ecco il metodo ricorsivo per determinare la soluzione:
Data l’equazione ![]() , si cerchi un intervallo
, si cerchi un intervallo ![]() tale che
tale che ![]() .
.
- Calcolare
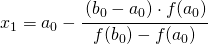
- Calcolare
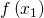
- Se
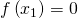 allora
allora 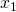 è proprio la soluzione e si termina il ciclo altrimenti si va al passo successivo.
è proprio la soluzione e si termina il ciclo altrimenti si va al passo successivo. - Solo al passo successivo al primo si calcola
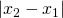 , se risulta minore della precisione voluta, si termina il ciclo uscendo.
, se risulta minore della precisione voluta, si termina il ciclo uscendo. - Se
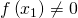 si deve scegliere il nuovo intervallo con il seguente criterio:
si deve scegliere il nuovo intervallo con il seguente criterio:
se ![]() allora
allora ![]() ,
, ![]()
se ![]() allora
allora ![]() ,
, ![]()
6. Si torna al punto 1 con i nuovi intervalli.
Nel caso in cui il segno della derivata seconda mantenesse lo stesso segno (ossia la curva mantenesse la stessa concavità) nell’intervallo trovato, il procedimento si semplifica notevolmente e si ha la seguente ricorsione.
Se ![]()
allora
![]()
![]()
Se ![]()
allora
![]()
![]()
[:]
