[:it]
Una particella carica, posta in un campo elettrico possiede energia potenziale poiché il campo esercita una forza sulle particelle e quindi bisogna effettuare un lavoro per spostarla.
Energia potenziale –> capacità di un oggetto (o sistema) di trasformare la propria energia in un’altra forma di energia ad esempio energia cinetica o energia elettrica
Il concetto è molto simile a quello usato nella meccanica in cui un oggetto posto ad una certa altezza ha un’energia potenziale ![]() ; essa poi quando l’oggetto cade si può vedere come energia cinetica
; essa poi quando l’oggetto cade si può vedere come energia cinetica ![]() .
.
Il potenziale elettrico, in un punto, è definito come l’energia potenziale posseduta da una carica unitaria posta in quel punto: essa è una quantità scalare (significa non vettoriale ossia senza verso, direzione ma solo modulo).
![]() oppure
oppure ![]()
L’unità di misura è ![]() ossia Joule su Coulomb e viene chiamata Volt in onore dello scienziato Alessandro Volta.
ossia Joule su Coulomb e viene chiamata Volt in onore dello scienziato Alessandro Volta.
Si immagina che una carica q si sposti da un punto A ad un punto B in un campo elettrico.
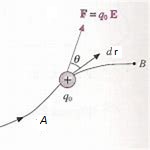
Allora si ha:
![]()
dove con ![]() intendo il lavoro fatto per muovere una carica unitaria da un punto ad un altro.
intendo il lavoro fatto per muovere una carica unitaria da un punto ad un altro.
(1) ![]()
La relazione precedente diventa, eliminando q:
(2) ![]()
Nel caso in cui A coincide con B ossia si ha un percorso chiuso l’integrale si annulla:
(3) ![]()
Indica che il lavoro svolto da un campo elettrostatico su una carica che percorre una linea chiusa è nullo. Pertanto il campo elettrostatico corrisponde ad un campo conservativo.
Calcolo pratico del potenziale
(4) ![]()
togliendo l’integrale da entrambi i termini si ha:
![]()
considerando il vettore ![]() posso esprimere la relazione che lega appunto il potenziale elettrico con il campo elettrico e la sua posizione nello spazio.
posso esprimere la relazione che lega appunto il potenziale elettrico con il campo elettrico e la sua posizione nello spazio.
![]()
![]()
![]()
In termini compatti e matematici la relazione precedente si può esprime:
![]()
ossia si legge che E è il gradiente del potenziale. Il simbolo ![]() si chiama nabla.
si chiama nabla.
Il gradiente esprime la variazione di una grandezza fisica scalare per unità di lunghezza in una data direzione.
Il gradiente trasforma uno scalare in un vettore.
CONCLUSIONI
Per stimare il campo elettrico tra due punti distanti d si usa la relazione precedente che diventa:
![]() [:]
[:]
