Principio delle probabilità totali

Yves Tanguy

• Due eventi sono incompatibili quando la loro probabilità non dipende dal fatto che accada o l’uno o l’altro.

Esempio: nell’estrazione di una carta da un mazzo di 40 carte, prendiamo in considerazione gli eventi:

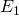1. : la carta estratta è un re;
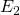2. : la carta estratta è un asso;
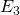3. : la carta estratta è un re o un asso.

1. Essendoci quattro re su un mazzo di 40

2. Essendoci quattro assi su un mazzo di 40

3. In questo caso sommo semplicemente i due eventi

• Due eventi sono compatibili se essi sono possono capitare contemporaneamente.

Esempio: nell’estrazione di una carta da un mazzo di 40 carte, prendiamo in considerazione gli eventi:

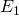1. : la carta estratta è un re
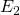2. : la carta estratta è una carta di cuori;
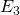3. : la carta estratta è un re o una carta di cuori

1. Essendoci quattro re su un mazzo di 40

2.Ci sono 10 carte di cuori per cui

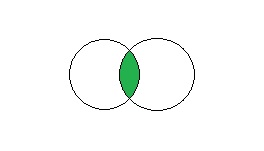
3. Nel terzo caso i casi favorevoli sono costituiti da 10 carte di cuori sommando i quattro re a cui devo sottrarre il caso in cui entrambi gli eventi possano capitare

In pratica si è in questa situazione in cui si deve sottrarre la contemporaneità degli eventi che altrimenti si conterebbero due volte:

in quanto ho sottratto la probabilità che l’evento sia una carta di cuori e che sia proprio un re.