
Vladimir Kush
Per sviluppare questi esercizi ricordo questi tre teoremi:
2. ![Rendered by QuickLaTeX.com \cfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\cfrac{a}{b}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-72a4779832adecc9db54627aff579e61_l3.png)
3. ![]()
Esercizi per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. |
|
| 6.6. |
|
| 6.7. |
|
| 6.8. |
|
| 6.9. |
|
| 6.10. |
|
| 6.11. |
|
| 6.12. |
|
| 6.12. |
|
| 6.13. |
Esercizi per un livello discreto (7):
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
| 7.4. |
|
| 7.5. |
|
| 7.6. |
![Rendered by QuickLaTeX.com \left [ \sqrt[3]{\cfrac{3}{16}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-26c97c3c1e73806b4efe438114e712dc_l3.png) |
| 7.7. |
|
7.8. ![Rendered by QuickLaTeX.com \sqrt[4]{\cfrac{9a^2b^4}{16c^6}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f10b03216b38445efffe2dd12bd5369f_l3.png) |
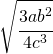 |
Esercizi per un buon livello
8.1. ![Rendered by QuickLaTeX.com \sqrt[4]{\cfrac{9}{16}+\cfrac{3}{2}+1}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-faee1149f7b9e8ae04313342cb2e71f2_l3.png) |
|
8.2. ![Rendered by QuickLaTeX.com \sqrt[6]{\cfrac{25}{9}-\cfrac{10}{3}+1}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-728aac4ec645636813f7a66481d305f6_l3.png) |
|
8.3. ![Rendered by QuickLaTeX.com \sqrt[2]{\cfrac{9}{49}+\cfrac{12}{7}+4}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-057c824034125a2021e9350be7484684_l3.png) |
Esercizi per un livello quasi ottimo (9)
| 9.1. |
|
| 9.2. |
Per un livello ottimo (10)
10.1. ![Rendered by QuickLaTeX.com \sqrt[6]{\cfrac{x^2-10x+25}{x^2-8xy+16y^2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f64a34efd752c1499f92daa202280468_l3.png) |
![Rendered by QuickLaTeX.com \left [\sqrt[3]{\cfrac{x-5}{x-4y}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c36847a763bf12a84b44dd7b03aa530e_l3.png) |
10.2. ![Rendered by QuickLaTeX.com \sqrt[9]{\cfrac{27a^3b^6}{\left ( 81a^2-18a+1 \right )^3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-25f05ba22d0f46215979fa4ec827a23e_l3.png) |
![Rendered by QuickLaTeX.com \left [ \cfrac{3ab^2}{\left ( 9a-1 \right )^2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-22dadf3866a664b2c64062d013cdfc69_l3.png) |
