I sistemi di equazione sono più utili di quanto si possa pensare per risolvere problemi di uso quotidiano.
Per farlo vi sono alcuni metodi; cercherò di spiegare quelli più comunemente usati.
Questa immagine rappresenta d’avvero quello che si può intendere per sistemi di equazione. Una mano non può esistere senza l’altra; è uguale a quello che capita con i sistemi di equazione di primo grado.
Espongo qua un problema che sarebbe ideale per i sistemi di disequazione ma che trova una prima applicazione anche nei sistemi di equazione lineare:
una persona noleggia un’auto e va in due agenzie di noleggio la A e la B con la seguente tariffa:
- A chiede una quota fissa di 45€ al giorno più 0,25€ per ogni chilometro percorso
- B chiede una quota fissa di 63€ al giorno più 0,18€ per ogni chilometro percorso.
Il problema che mi pongo è sicuramente qual è scelta migliore.
Un altro problema è tipico della settimana enigmistica ma potrebbe dare un senso a cimentarsi a risolvere un sistema di equazioni di primo grado:
Se Luigi desse a Carlo metà del suo denaro, Carlo avrebbe in totale la somma di 150€. Se invece fosse Carlo a dare a Luigi 1/3 di quanto ha, allora sarebbe Luigi ad avere la stessa somma. Quanto hanno Luigi e Carlo?
Adesso mi preme di dare delle tecniche di risoluzioni generali:
si danno dei nomi tanto per distinguerle: il metodo della sostituzione, quello dell’addizione, e quello del confronto. Quando affronterò lo studio dei punti in cui delle curve si toccano nello spazio si vedrà quanto utile è conoscere tali metodi.
Ecco il primo sistema semplice ma tanto per cominciare va bene:
![]()
METODO DELL’ADDIZIONE
Mi devo solo ricordare come faccio le somme in colonna. Unica avvertenza: incolonnare bene, prima le x poi le y e poi i numeri; importantissimo non sbagliare l’incolonnamento!
Lo scopo è quello di far sparire una delle due incognite o la x o la y:
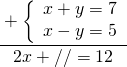
Ritrovandomi l’equazione
![]()
che mi fornisce come soluzione
![]()
Nel caso in cui non fosse chiaro è sufficiente andare al post sulla risoluzione delle equazioni di primo grado (equazioni di primo grado). Trovata la x è sufficiente adesso sostituire il valore della x o nella prima o nella seconda equazione
Oppure si può trovare la y moltiplicando per -1 la seconda equazione trovandomi in questa situazione:
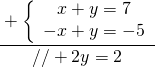
e risolvo la semplice equazione di primo grado:
![]()
che ha come soluzione
![]() .
.

sono molto confuso e non riesco a capire