 Questo problema è stato tratto da La settimana Enigmistica del 24 dicembre 2015 quesito 7063 e dato alla verifica sui sistemi d’equazione alle classi di seconda superiore il 13 gennaio 2016.
Questo problema è stato tratto da La settimana Enigmistica del 24 dicembre 2015 quesito 7063 e dato alla verifica sui sistemi d’equazione alle classi di seconda superiore il 13 gennaio 2016.
“Biagio, Fulvio e Giacomo sono tre studenti universitari di matematica. Per raggranellare qualche soldo, nel mese di dicembre, si sono ritrovati a lavorare in un grande magazzino, nel reparto degli addobbi natalizi. Forti della loro padronanza dei numeri, a volte si divertivano a mettere qualcuno in difficoltà. Così, a un signore troppo pignolo,
- Biagio ha risposto: “Si, 7 palline e 5 stelle costano come 6 angioletti”
- Fulvio ha rincarato: “Oppure, se vuole, 4 palline più 9 angioletti hanno lo stesso prezzo di 5 stelle”.
- Giacomo interviene: “E 6 angioletti e 3 stelle valgono come 4 palline
Ma quando il cliente, frastornato, è giunto alla cassa, si è scoperto che uno di loro aveva mentito mentre gli altri due avevano dato informazioni corrette.
Chi ha dato informazioni errate?
Soluzione:
Si imposta un sistema di equazione con
p palline
a angioletti
s stelle
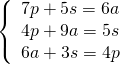
Adesso li ordino ed ho:
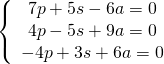
Suppongo che le prime due ossia Biagio e Fulvio abbiano detto la verità e le sommo:
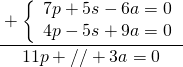
che risolta dà:
![]()
che è impossibile in quanto le palline non possono dare un costo negativo.
Per cui o Biagio o Fulvio ha detto il falso!
Adesso sommo Fulvio e Giacomo
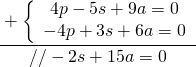
ossia
![]()
che è possibile.
Per cui chi dice il falso è Biagio.
