Per rispondere è necessario aver compreso fino in fondo la definizione di parabola, ellisse, iperbole, circonferenza ossia come opportuni luoghi geometrici che soddisfano a delle condizioni che determinano le relazioni tra x e y.
Nel caso specifico il centro delle nostre generiche circonferenze giacciono tutte sulla parabola quindi il centro ha coordinate:
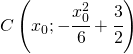 e raggio
e raggio ![]()
quindi la circonferenza generica ha equazione:
(1) 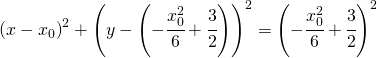
Essa è proprio tangente all’asse delle ascisse in quanto ponendo ![]() si osserva che tocca l’asse solo in un punto generico
si osserva che tocca l’asse solo in un punto generico ![]() infatti la (1) diventa:
infatti la (1) diventa: ![]() che è un prodotto notevole.
che è un prodotto notevole.
Mettendolo poi in sistema con l’equazione:
![]() si ha ancora una soluzione per cui è dimostrato l’asserzione iniziale.
si ha ancora una soluzione per cui è dimostrato l’asserzione iniziale.
La seconda parte del quesito richiede di mettere a sistema la (1) con la circonferenza:
![]() e si trova la circonferenza voluta.
e si trova la circonferenza voluta.

