Si calcolino le derivate prime delle seguenti funzioni ed il relativo dominio.
Per un livello sufficiente (6)
| 6.1. |
|
| 6.2. |
Per un livello discreto (7)
| 7.1. |
![Rendered by QuickLaTeX.com \left [y^{'}=-\cfrac{1}{x^2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-95d7e93f5fef6dffb7a19e2f44222eca_l3.png) |
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
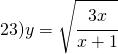 .
.

Si calcolino le derivate prime delle seguenti funzioni ed il relativo dominio.
Per un livello sufficiente (6)
| 6.1. |
|
| 6.2. |
Per un livello discreto (7)
| 7.1. |
![Rendered by QuickLaTeX.com \left [y^{'}=-\cfrac{1}{x^2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-95d7e93f5fef6dffb7a19e2f44222eca_l3.png) |
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
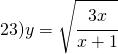 .
.
Per l’esercizio 1 qual è il dominio?