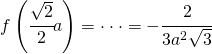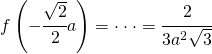Maturità 2019: secondo problema – terzo punto

Pubblicato il 21 Giugno 2019 da admin

Per a > 0, si consideri la funzione $f: \mathbb{R}\rightarrow \mathbb{R}$ deﬁnita da:

$f(t)=-\cfrac{t}{\sqrt{\left ( t^2+a^2 \right )^3}}$

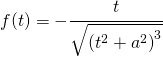
Verificare che:

$F(t)=\cfrac{1}{\sqrt{t^{2}+a^{2}}}-\cfrac{1}{a}$

è la primitiva di $f$ il cui graﬁco passa per l’origine.

Studiare la funzione 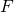$F$ individuandone eventuali simmetrie, asintoti, estremi.
Provare che 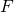$F$ presenta due ﬂessi nei punti di ascisse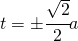 $t=\pm \cfrac{\sqrt{2}}{2}a$
Determinare le pendenze delle rette tangenti al graﬁco di $F$ in tali punti.

Prerequisiti

saper fare la derivata di una funzione fratta
studio di funzione completo
aver capito il concetto di derivata

Sviluppo

Primo punto

Riscrivo la $F$ per facilitarmi la sua derivata:

$F(t)=\cfrac{1}{\sqrt{t^{2}+a^{2}}}-\cfrac{1}{a}=\left ( t^{2}+a^{2} \right )^{-\frac{1}{2}}-\cfrac{1}{a}$

$F'(t)=-\frac{1}{2}\left ( t^{2}+a^{2} \right )^{-\frac{3}{2}}\cdot 2t$

$F'(t)=f(t)$

inoltre $F(0)=0$

Secondo punto

Dominio è tutto $\mathbb{R}$

La funzione è pari, infatti:

$F(t)=F(-t)$ quindi è simmetrica rispetto l’asse x.

Non vi sono asintoti orizzontali.

$\underset{x\rightarrow+\infty}{lim}\cfrac{1}{\sqrt{ t^2+a^2 }}-\frac{1}{a}=-\frac{1}{a}$

Vi è asintoto orizzontale in

$y=-\frac{1}{a}$

$F'(t)=-\frac{1}{2}\left ( t^{2}+a^{2} \right )^{-\frac{3}{2}}\cdot 2t$

e si annulla solo in $t=0$ che è proprio il punto di massimo osservando il segno della derivata prima.

Ecco il grafico della funzione:

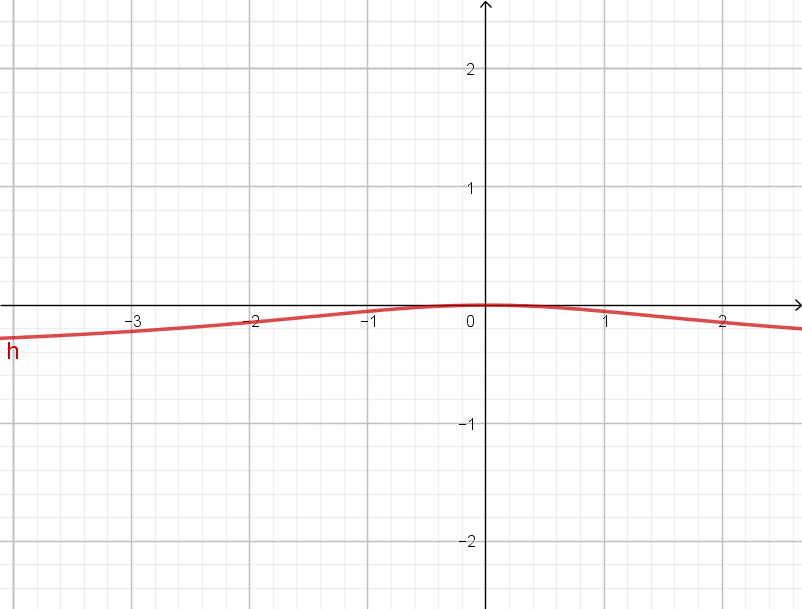
Terzo punto

Faccio la derivata prima della derivata prima per determinare i flessi:

$F'(t)=-\cfrac{t}{\sqrt{\left ( t^2+a^2 \right )^3}}=-t\cdot \left (t^2+a^2 \right )^{-\frac{3}{2}}$

$F''(t)=-\left (t^2+a^2 \right )^{-\frac{3}{2}}-t\cdot \left ( -\frac{3}{2} \right )\left (t^2+a^2 \right )^{-\frac{5}{2}}\cdot 2t=-\cfrac{1}{\sqrt{\left (t^2+a^2 \right )^3}}+\cfrac{3t^2}{\left (t^2+a^2 \right )^5}$

$F''(t)=\cfrac{-t^2-a^2+3t^2}{\left (t^2+a^2 \right )^5}$

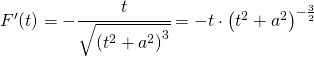
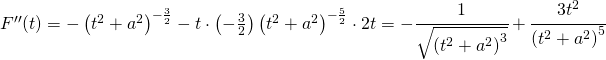
che si annulla proprio in:

$t=\pm \cfrac{\sqrt{2}}{2}a$

Quarto punto

E’ sufficiente sostituire i valori dei flessi nella derivata prima:

$f\left ( \cfrac{\sqrt{2}}{2}a \right )=\cdot \cdot \cdot =-\cfrac{2}{3a^2\sqrt{3}}$

$f\left (- \cfrac{\sqrt{2}}{2}a \right )=\cdot \cdot \cdot =\cfrac{2}{3a^2\sqrt{3}}$

Questa voce è stata pubblicata in Senza categoria. Contrassegna il permalink.

Lascia un commento Annulla risposta