Jacek jerka
Nell’introduzione avevo accennato al fatto che studiare cosa accade ad una funzione nell’intorno di un punto significa studiare il limite a destra e a sinistra.Tale studio, com’è consuetudine, in analisi si riassume in tali forme:
(1) 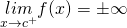
(2) 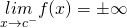
la (1) descrive il fatto che si studia l’andamento della funzione quando ci si avvicina al valore  provenendo da destra.
provenendo da destra.
la (2) descrive il fatto che si studia l’andamento della funzione quando ci si avvicina al valore  provenendo da sinistra.
provenendo da sinistra.
Ad esempio: assumo che 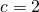 allora provenire da sinistra significa prendere i seguenti valori: 1,8; 1,9; 1,91 e così via; provenire da destra significa prendere i seguenti valori 2,2; 2,1; 2,001 e così via.
allora provenire da sinistra significa prendere i seguenti valori: 1,8; 1,9; 1,91 e così via; provenire da destra significa prendere i seguenti valori 2,2; 2,1; 2,001 e così via.
Ancora provenire da destra significa prendere valori 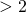 mentre provenire da sinistra significa prendere valori
mentre provenire da sinistra significa prendere valori 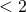 .
.
Per capire se la funzione assume un valore 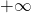 o
o  si deve studiare il segno della funzione in un intorno del valore a cui tende la
si deve studiare il segno della funzione in un intorno del valore a cui tende la 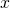 .
.
Ecco un esempio:
(3) 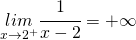
(4) 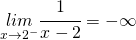
Infatti:
– il dominio è tutto 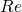 escludendo il valore in cui si annulla il denominatore ossia 2.
escludendo il valore in cui si annulla il denominatore ossia 2.
– devo studiare la seguente disequazione:
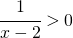 .
.
Per 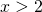 la funzione è positiva mentre per
la funzione è positiva mentre per  la funzione è negativa.
la funzione è negativa.
La regola è:
per studiare i limiti nella forma (1) e (2) si deve studiare la disequazione della funzione di cui si deve studiare il limite.
Tale regola giustifica il continuo studio delle disequazioni frazionarie negli anni scolastici precedenti!
Quindi si ha sempre un asintoto verticale ma la funzione ha un andamento diverso.
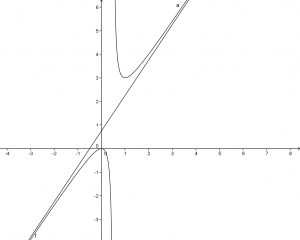
Il grafico della funzione:
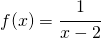 è:
è:
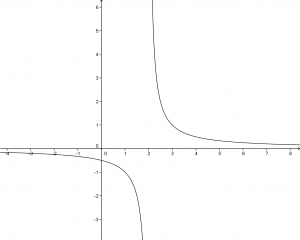
Si nota che:
all’avvicinarsi a 2 da destra la funzione assume valori sempre positivi al limite infinitesimamente positivi;
all’avvicinarsi a 2 da sinistra la funzione assume valori sempre negativi al limite infinitesimamente negativi.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() [:en]
[:en]![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() [:de]
[:de]![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() [:]
[:]



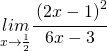


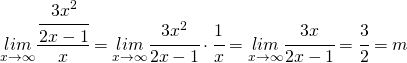
![Rendered by QuickLaTeX.com \underset{x\rightarrow\infty}{lim}\left[\cfrac{3x^{2}}{2x-1}-\cfrac{3}{2}x\right]=\underset{x\rightarrow\infty}{lim}\cfrac{6x^{2}-3x(2x-1)}{(2x-1)\cdot2}=\underset{x\rightarrow\infty}{lim}\cfrac{6x^{2}-6x^{2}+3x}{(2x-1)\cdot2}=\underset{x\rightarrow\infty}{lim}\cfrac{3x}{4x-2}=\cfrac{3}{4}=q](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8c7607f686ead3f6506f65e7541a9133_l3.png)