Si può pedalare agevolmente su una bicicletta a ruote quadrate? A New York, al MoMath-Museum of Mthematics si può fare, in uno dei padiglioni dedicati al divertimento matematico
E’ però necessario che il profilo della pedana su cui il lato della ruota può scorrere soddisfi alcuni requisiti.
nella figura 2 è riportata una rappresentazione della situazione nel piano cartesiano Oxy: il quadrato di lato DE=2 (in opportune unità di misura) e di centro C rappresenta la ruota della bicicletta, il grafico della funzione ![]() rappresenta il profilo della pedana.
rappresenta il profilo della pedana.
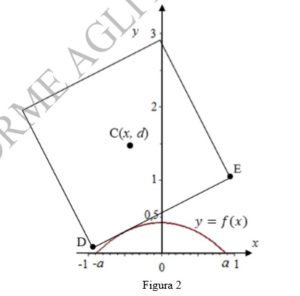
1) Sulla base delle informazioni ricavabili dal grafico in figura 2, mostra, con le opportune argomentazioni, che la funzione:
![]()
![]()
rappresenta adeguatamente il profilo della pedana per ![]() ; determina inoltre il valore degli estremi
; determina inoltre il valore degli estremi ![]() e
e ![]() dell’intervallo.
dell’intervallo.
Prerequisiti
- saper risolvere un’equazione esponenziale
- conoscere il logaritmo e le sue proprietà
- saper derivare una funzione esponenziale
- calcolare il massimo di una funzione
- saper risolvere una disequazione esponenziale
Sviluppo
Calcolo le intersezioni della funzione annullandola
(1) 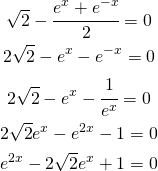
adesso pongo
(2) ![]()
e devo risolvere una semplice equazione di secondo grado:
(3) 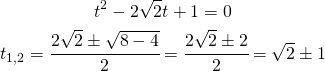
torno alla (2) con le soluzioni trovate e risolvo la relativa equazione esponenziale
(4) 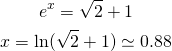
La prima intersezione è:
![]()
(5) 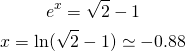
La seconda intersezione è:
![]()
Adesso calcolo la derivata prima e determino i punti di massimo o di minimo così da verificare che l’andamento della curva sia come quello della figura 2.
![]()
(6) ![]()
La annullo per verificare i potenziali punti di massimo o minimo
(7) ![]()
il metodo più veloce per risolverla è la loro rappresentazione grafica che permette poi anche di studiare subito il segno per determinare dove la funzione cresce o decresce.
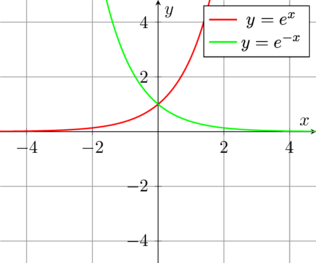
e si nota subito che l’unico punto in cui si intersecano è lo 0.
Tale punto è di massimo o di minimo?
Studio il segno della derivata prima.
sempre dal grafico si nota che ![]() è maggiore di
è maggiore di ![]() per
per ![]() ma essendoci il segno meno davanti alla derivata prima si ha il seguente grafico del segno:
ma essendoci il segno meno davanti alla derivata prima si ha il seguente grafico del segno:
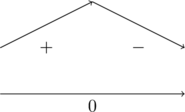
e quindi per ![]() si ha proprio un punto di massimo,
si ha proprio un punto di massimo,
![]()
ed il grafico della funzione è proprio quello della figura 2.
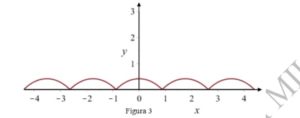
Per visualizzare il profilo completo della pedana sulla quale la bicicletta potrà muoversi, si affiancano varie copie del grafico della funzione ![]() relativo all’intervallo
relativo all’intervallo ![]() , come mostrato in figura 3.
, come mostrato in figura 3.
2) Perché la bicicletta possa procedere agevolmente sulla pedana è necessario che:
- a sinistra e a destra dei punti di non derivabilità i tratti del grafico siano ortogonali;
- la lunghezza del lato della ruota quadrata risulti pari alla lunghezza di una “gobba”, cioè dell’arco di curva di equazione
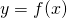 per
per ![Rendered by QuickLaTeX.com x\in \left [ -a;a \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9e9da677c480e72bf5e8d9bb243f9eac_l3.png)
stabilisci se tali condizioni sono verificate. In generale, la lunghezza dell’arco di curva avente equazione ![]() compreso tra le ascisse
compreso tra le ascisse ![]() e
e ![]() è data da
è data da
(8) ![]()
Prerequisiti
- riconoscere i punti di non derivabilità di una funzione
- essere in grado di fare la derivata
- collegamento tra il valore della derivata e l’inclinazione della retta tangente in quel punto.
- essere in grado di sviluppare un integrale definito
- proprietà dei logaritmi
- ottima manualità con i radicali e i prodotti notevoli con i radicali stessi
- molto precisi ed attenzione nei segni
Sviluppo
I punti di non derivabilità sono quelli in cui la curva interseca l’asse delle ascisse in quanto il valore della derivata destra e della derivata sinistra è differente. Nel caso specifico però calcolando la derivata in quei due punti posso avere il coefficiente angolare delle rette tangenti. Se esse sono tra loro opposte e reciproche allora i tratti del grafico di non derivabilità sono ortogonali.
Avevo già calcolato la derivata in (6) e risulta:
![]()
La calcolo nei punti di intersezione già precedentemente trovati in (4) e (5) ossia:
![]()
![]()
(9) ![]()
ma partendo dalla definizione stessa di logaritmo
(10) ![]()
(11) 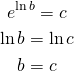
quindi
(12) ![]()
ed utilizzo anche la seguente proprietà:
(13) ![]()
che applicata in questo caso diventa:
(14) ![]()
Utilizzo la (12) e la (14) nella (9) e diventa:
(15) 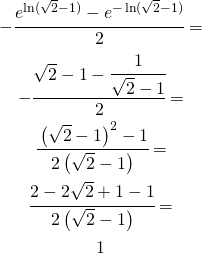
seguendo lo stesso procedimento per l’altro punto d’intersezione
(16) ![]()
che forniscono il valore del coefficiente angolare delle rette tangenti e perché siano ortogonali deve valere la relazione:
![]()
ed infatti è soddisfatta:
(17) ![]()
Nella seconda parte del quesito si chiedeva di calcolare un semplice integrale definito per calcolare la lunghezza dell’arco di curva, utilizzando il suggerimento, e porlo uguale alla lunghezza del quadrato che dato dal testo e vale 2.
Analiticamente deve valere questa condizione:
(18) 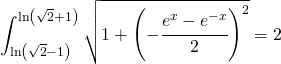
Sviluppo l’argomento della radice
(19) 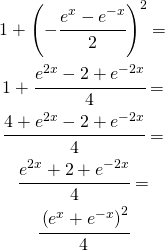
e l’integrale definito diventa:
(20) 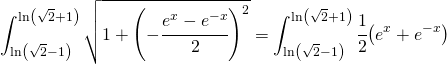
la cui primitiva diventa:
(21) 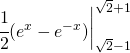
utilizzando tutte le proprietà dalla (10) alla (14) l’integrale definito diventa:
(22) ![Rendered by QuickLaTeX.com \begin{gather*} \cfrac{1}{2}\left [ \sqrt{2}+1- \cfrac{1}{\sqrt{2}+1}- \left ( \sqrt{2}-1-\cfrac{1}{\sqrt{2}-1} \right )\right ] \\ \cfrac{1}{2}\left [ \sqrt{2}+1- \cfrac{1}{\sqrt{2}+1}- \sqrt{2}+1+\cfrac{1}{\sqrt{2}-1} \right ] \\ \cfrac{1}{2}\left [ 2-\cfrac{1}{\sqrt{2}+1}+\cfrac{1}{\sqrt{2}-1} \right ] \\ \cfrac{1}{2}\left [ \cfrac{2\left ( \sqrt{2}+1 \right )\left ( \sqrt{2}-1 \right )-\sqrt{2}+1+\sqrt{2}+1}{\left ( \sqrt{2}+1 \right )\left ( \sqrt{2}-1 \right )} \right ] \\ \cfrac{1}{2}\left [ \cfrac{2+2}{1} \right ]=2 \end{gather*}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-1f7f4c2e9b0b267c4f8e6bcba8771d46_l3.png)
ed ho verificato l’affermazione del problema.
3) Consideriamo la similitudine dei triangoli rettangoli ACL e ALM in figura 4, e ricordando il significato geometrico della derivata, verifica che il valore dell’ordinata ![]() del centro della ruota si mantiene costante durante il moto. Pertanto, al ciclista sembra di muoversi su una superficie piana.
del centro della ruota si mantiene costante durante il moto. Pertanto, al ciclista sembra di muoversi su una superficie piana.
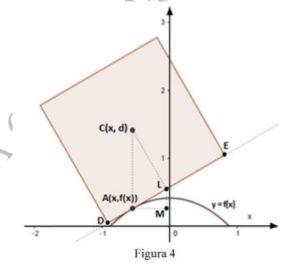
Prerequisiti
- conoscenza delle proprietà dei triangoli simili
- conoscere bene la definizione di derivata e quindi inclinazione di una retta
- conoscenza del teorema di Pitagora.
Sviluppo
Sfruttando la proprietà dei triangoli simili posso dire che:
(23) ![]()
(24) ![]()
questo rapporto è proprio il valore della derivata lungo la curva.
(25) ![]()
Applico Pitagora al triangolo DLC
(26) ![]()
(27) ![]()
in quanto metà del lato
(28) ![]()
utilizzando (25), la (27) e la (28) inserendola nella (26) ho:
(29) ![]()
Adesso sostituisco i valori della derivata e della funzione ed ho:
(30) 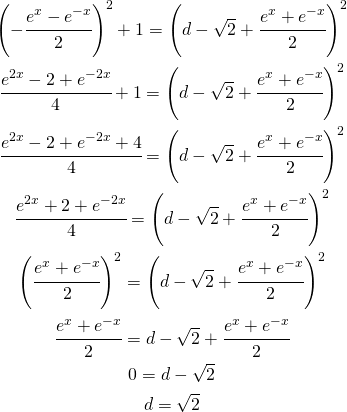
e quindi ![]() rimane costante.
rimane costante.
Anche il grafico della funzione:
![]() per
per ![]()
se replicato varie volte, può rappresentare il profilo di una pedana adatta a essere percorsa da una bicicletta con ruote molto particolari, aventi la forma di un poligono regolare.
4) Individua tale poligono regolare, motivando la risposta
Prerequisiti
- relazione tra derivata ed inclinazione della retta
- conoscere le proprietà dei logaritmi
- saper bene le derivate
Sviluppo
L’ipotesi di partenza già mi dice che questo è un nuovo profilo per cui non devo fare tutti i passaggi precedenti e sempre nell’ipotesi gli estremi in cui è definita la funzione rappresentano le intersezioni con gli assi. Si può fare la verifica ma è sicuramente ridondante.
Allora calcolo la derivata prima nei punti d’intersezione.
La derivata prima è sempre la (6) che riporto:
![]()
La devo calcolare nei punti d’intersezione:
(31) 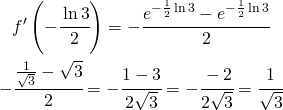
in maniera analoga con l’altro punto d’intersezione e l’inclinazione varrà:
(32) 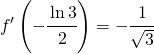
Avere il valore dell’inclinazione della retta è come avere il valore della tangente di cui devo trovare il relativo angolo:
![]()
Per cui l’angolo che forma la retta con l’asse delle ascisse vale esattamente
![]()
Anche l’altra retta forma un angolo di ![]() per cui l’angolo tra i lati di questo poligono è
per cui l’angolo tra i lati di questo poligono è ![]()
L’unico poligono che presenta tale angolo tra i sui lati è un esagono.
